Let S(n, k) be a number of states of the game where two bots together can make n moves and first bot can make k moves itself (k ≤ n). It is obvious that S(n, 0) = S(n, n) = n + 1. S(n, k) can be defined by the simple recurrence relation S(n, k) = 1 + S(n - 1, k - 1) + S(n - 1, k). Hence S(n, k) = F(n, k) - 1 where F(n, k) is defined by recurrence relation F(n, k) = F(n - 1, k - 1) + F(n - 1, k). It is a well-known formula for binomial coefficients. So 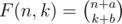 where a and b are some constants. They can be found using the foregoing equation for S(n, 0): a = 2, b = 1. Hence
where a and b are some constants. They can be found using the foregoing equation for S(n, 0): a = 2, b = 1. Hence 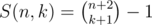 . But in the optimal winning strategy both bots make exactly N moves each so n = 2N and k = N. Finally we have that the number of possible states is equal to
. But in the optimal winning strategy both bots make exactly N moves each so n = 2N and k = N. Finally we have that the number of possible states is equal to
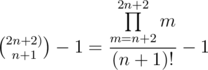 .
.










I found the same formula for this problem but by analysing a large table.
Do you know any sources where the proof for the formula f(i,j) = f(i-1,j-1) + f(i-1,j) = combination(i+a,j+b)? I could not google it since I dunno how to search with mathematical formula.
I came up with same approach, so I will try to explain how it works. You know, that F(n,0)=S(n,0)+1=n+2=C(n+2,1); F(n,n)=S(n,n)+1=n+2=C(n+2,1)=C(n+2,n+1). We know, that F has the same recurrence relation as C. Let's try calculating some other values. For example F(2,1)=F(1,0)+F(1,1)=C(1+2,1)+C(1+2,1+1)=C(3,1)+C(3,2)=C(4,2). So the good guess would be F(n,k)=C(n+2,k+1). You can prove it by induction.
Actually I am prone to disagree that recurrence relation will necessarily result in combination(i+a, j+b) as a solution. It really depends on boundary values. It could have been twice the combination of some values or even not a combination at all. But it always seems to be some sum (finite or infinite) of combinations
why S(n,k)=F(n,k)-1; please explain it?