ken_love_rin's blog

COCI 2015
By ken_love_rin, history, 9 years ago, In English

can you help me?

You are given an array of N integers. Find a consecutive subsequence of numbers of the length at least K that has the maximal possible average. Please note: the average of a subsequence is the sum of all the numbers in the subsequence divided by its length. INPUT The first line of input contains two integers N (1 6 N 63 · 105) and K (16 K 6 N). The second line of input contains N integers ai (16 ai 6106). OUTPUT The first and only line of output must contain the maximal possible average. An absolute deviation of ±0.001 from the official solution is permitted. SCORING In test cases worth 30% of total points, it will hold that N is not larger than 5000. SAMPLE TESTS

input
  6 3 
  7 1 2 1 3 6
  output
  3.333333
  • Vote: I like it
  • +3
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Auto comment: topic has been updated by ken_love_rin (previous revision, new revision, compare).

→ Reply
»
9 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Binary search the answer. You need to answer the question: is there a subsequence of length at least K that has average  ≥ x. Now the condition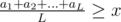 is equivalent to (a1 - x) + (a2 - x) + ... + (aL - x) ≥ 0. So now transform each of the elements of your sequence to ai - x and find if there is a subsequence of length at least K that has a positive sum.

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

There was a problem on USACO which has very similar solution link

editorial

→ Reply
»
9 years ago, # |
  Vote: I like it +2 Vote: I do not like it

You can solve this problem with (binary search)+(partial sum)+(math) firstly we can select x use with binary search then (a1...aL)/L>=x (a1...aL)-(LX)>=0 (a1-x)+(a2-x)...+(aL-x)>=0 then you will be find at least k length sum of numbers will be greater and equal than 0 You can do this operation with partial sum Then you can solve this problem!!!

→ Reply