Problm 1 : Raising Bacteria
Write down x into its binary form. If the ith least significant bit is 1 and x contains n bits, we put one bacteria into this box in the morning of (n + 1 - i)th day. Then at the noon of the nth day, the box will contain x bacteria. So the answer is the number of ones in the binary form of x.
Problem 2 : Finding Team Member
Sort all possible combinations from high strength to low strength. Then iterator all combinations. If two people in a combination still are not contained in any team. then we make these two people as a team.
Problem 3 : A Problem about Polyline
If point (a,b) is located on the up slope/ down slope of this polyline. Then the polyline will pass the point (a - b,0)/(a + b,0).(we call (a - b) or (a + b) as c afterwards) And we can derive that c / (2 * x) should be a positive integer. Another condition we need to satisfy is that x must be larger than or equal to b. It’s easy to show that when those two conditions are satisfied, then the polyline will pass the point (a,b).
Formally speaking in math : Let c / (2 * x) = y Then we have x = c / (2 * y) ≥ b and we want to find the maximum integer y. After some more math derivation, we can get the answer is 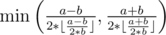 . Besides, the only case of no solution is when a < b.
. Besides, the only case of no solution is when a < b.
In fact, 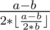 always dosn't exist or larger than
always dosn't exist or larger than 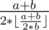 .
.
author's code:
#include <bits/stdc++.h>
typedef long long LL;
using namespace std;
int main(){
LL a,b;
cin>>a>>b;
if(a<b)puts("-1");
else printf("%.12f\n",(a+b)/(2.*((a+b)/(2*b))));
return 0;
}
Problem 4 : Or Game
We can describe a strategy as multiplying ai by x ti times so ai will become bi = ai * xti and sum of all ti will be equals to k. The fact is there must be a ti equal to k and all other ti equals to 0. If not, we can choose the largest number bj in sequence b, and change the strategy so that tj = k and all other tj = 0. The change will make the highest bit 1 of bj become higher so the or-ed result would be higher.
After knowing the fact, We can iterator all number in sequence a and multiply it by xk and find the maximum value of our target between them. There are several method to do it in lower time complexity. You can check the sample code we provide.(I believe you can understand it quickly.)
author's code:
#include<cstdio>
#include<algorithm>
using namespace std;
const int SIZE = 2e5+2;
long long a[SIZE],prefix[SIZE],suffix[SIZE];
int main(){
int n,k,x;
scanf("%d%d%d", &n, &k, &x);
long long mul=1;
while(k--)
mul *= x;
for(int i = 1; i <= n; i++)
scanf("%I64d", &a[i]);
for(int i = 1; i <= n; i++)
prefix[i] = prefix[i-1] | a[i];
for(int i = n; i > 0; i--)
suffix[i] = suffix[i+1] | a[i];
long long ans = 0;
for(int i= 1; i <= n; i++)
ans = max(ans, prefix[i-1] | (a[i] * mul) | suffix[i+1]);
printf("%I64d\n",ans);
}
Problem 5 : Weakness and Poorness
Let 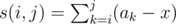 , we can write down the definition of poorness formally as
, we can write down the definition of poorness formally as
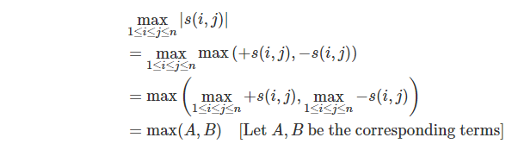
. It's easy to see that A is a strictly decreasing function of x, and B is a strictly increasing function of x. Thus the minimum of max(A, B) can be found using binary or ternary search. The time complexity is 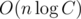 ,
,
Now here give people geometry viewpoint of this problem:
let 
We plot n + 1 straight line y = i * x + bi in the plane for i from 0 to n.
We can discover when you are given x. The weakness will be (y coordinator of highest line at x) — (y coordinator of lowest line at x).
So we only need to consider the upper convex hull and the lower convex hull of all lines. And the target x value will be one of the intersection of these convex hull.
Because you can get these line in order of their slope value. we can use stack to get the convex hulls in O(n).
author's code : this (using binary search)
code of author's friend (using stack to handle convexhull with O(n), have more precision)
Problem 6 : LCS again
Followings are solution in short. Considering the LCS dp table lcs[x][y] which denotes the LCS value of first x characters of S and first y characters of T. If we know lcs[n][n] = n - 1, then we only concern values in the table which abs(x - y) ≤ 1 and all value of lcs[x][y] must be min(x, y) or min(x, y) - 1. So each row contains only 8 states(In fact,three states among these states will never be used), we can do dp on it row by row with time complexity O(n).
There is another not dp method. You can refer this comment.
author's code:
#include <bits/stdc++.h>
#define SZ(X) ((int)(X).size())
#define ALL(X) (X).begin(), (X).end()
#define REP(I, N) for (int I = 0; I < (N); ++I)
#define REPP(I, A, B) for (int I = (A); I < (B); ++I)
#define RI(X) scanf("%d", &(X))
#define RII(X, Y) scanf("%d%d", &(X), &(Y))
#define RIII(X, Y, Z) scanf("%d%d%d", &(X), &(Y), &(Z))
#define DRI(X) int (X); scanf("%d", &X)
#define DRII(X, Y) int X, Y; scanf("%d%d", &X, &Y)
#define DRIII(X, Y, Z) int X, Y, Z; scanf("%d%d%d", &X, &Y, &Z)
#define RS(X) scanf("%s", (X))
#define CASET int ___T, case_n = 1; scanf("%d ", &___T); while (___T-- > 0)
#define MP make_pair
#define PB push_back
#define MS0(X) memset((X), 0, sizeof((X)))
#define MS1(X) memset((X), -1, sizeof((X)))
#define LEN(X) strlen(X)
#define PII pair<int,int>
#define VPII vector<pair<int,int> >
#define PLL pair<long long,long long>
#define F first
#define S second
typedef long long LL;
using namespace std;
const int MOD = 1e9+7;
const int SIZE = 1e5+10;
// template end here
LL dp[SIZE][8];
char s[SIZE];
int get_bit(int x,int v){return (x>>v)&1;}
int main(){
DRII(n,m);
RS(s+1);
REPP(i,1,n+1)s[i]-='a';
s[n+1]=-1;
REP(i,m){
int state=1;
if(i==s[1])state|=2;
if(i==s[1]||i==s[2])state|=4;
dp[1][state]++;
}
REPP(i,2,n+1){
REP(j,8){
int d[4]={i-3+get_bit(j,0),i-2+get_bit(j,1),i-2+get_bit(j,2)};
REP(k,m){
int d2[4]={};
REPP(l,1,4){
if(s[i-2+l]==k)d2[l]=d[l-1]+1;
else d2[l]=max(d2[l-1],d[l]);
}
if(d2[1]>=i-2&&min(d2[2],d2[3])>=i-1)dp[i][(d2[1]-(i-2))|((d2[2]-(i-1))<<1)|((d2[3]-(i-1))<<2)]+=dp[i-1][j];
}
}
}
printf("%lld\n",dp[n][0]+dp[n][1]+dp[n][4]+dp[n][5]);
return 0;
}
Problem 7 : Walking!
Since there is only one person, it’s not hard to show the difference between the number of left footprints and the number of right footprints is at most one.
For a particular possible time order of a sequence of footprints, if there are k backward steps, we can easily divide all footprints into at most k + 1 subsequences without backward steps. Then you might guess that another direction of the induction is also true.That is, we can combine any k + 1 subsequence without backward steps into a whole sequence contains at most k backward steps. Your guess is correct !
Now we demostrate the process of combining those subsequences.
We only concern the first step and the last step of a divided subsequence. There are four possible combinations, we denote them as LL/LR/RL/RR subsequence separately(the first character is the type of the first step and the second character is the type of the second step).
Suppose the number of four types of subseueqnce(LL/LR/RL/RR) are A, B, C, D separately. We have abs(A - D) ≤ 1.
We can combine all RR, LL subsequeces in turn into one subsequenceswith at most A + D - 1 backward steps(the result may be of any of the four subsquence types). Now we have at most one LL or RR type subsequence.
Then we can combine all RL subsequence into only one RL subsequence with at most A - 1 backward steps easily. And so do LR subsequences. Now we want to combine the final RL and LR subsequences together. We could pick the last footprint among two subsequences, exclude it from the original subsequcne and append it at the tail of another subsequence. The move will not increase the number of backward step and the types of the two subsequences would become RR and LL ! We can easily combine them into one LR or RL subsequence now. If there is still a LL or RR type subsequence reamained. We can easily combine them, too.
So if we can divide all footprints into the least number of subsequences without backward steps. Then we have solved the problem. And this part can be done with greedy method.
Now we provide one possible greedy method:
Firstly, we translate this problem to a maximum matching problem on bipartite graph as following:
Take "RLLRRL" as example:
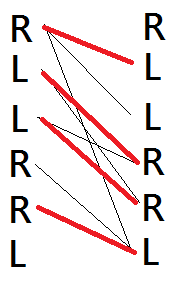
We split each footprint into two vertices which on is in left part and another is in right part.
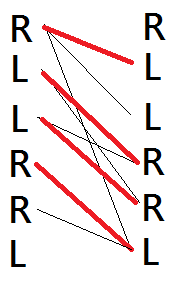
If two footprints is next to each other in resulted subsequnces, we will connect the left vertex of the former to right vertex of the latter in the corresponded matching. So the matching described in above left graph is subsequences: "RL-R--" and "--L-RL" and in above right graph is "RL-R-L" and "--L-R-". we can find that the number of subsequences is (number of footprints) — (value of matching).
Due to the graphs produced by this problem is very special, we can solve this bipartite matching as following:
Iterate each vertex in left part from top to bottom and find the uppermost vertex which is able to be matched in right part and connect them.
If we process this algorithm in "RLLRRL", the resulted matching is the above right graph.
Why the greedy method is correct? we can prove it by adjusting any maximum matching to our intended matching step by step. In each step, you can find the uppermost vertex the state of which is different to what we intend and change its state. I guess the mission of adjusting is not too hard for you to think out! Please solve it by yourself >_<
By the way, I believe there are also many other greedy methods will work. If your greedy method is different to author's. Don't feel strange.
Problem 8 : The Mirror Box
If we view the grid intersections alternatively colored by blue and red like this:
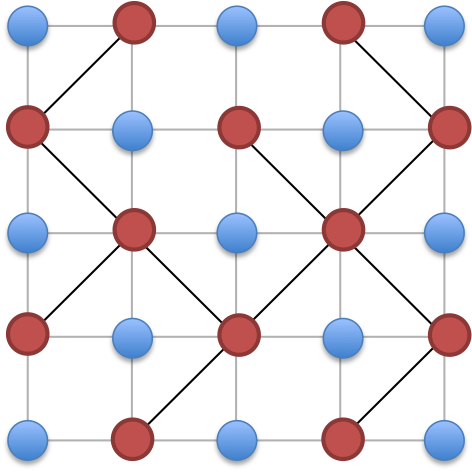
Then we know that the two conditions in the description are equivalent to a spanning tree in either entire red intersections or entire blue dots. So we can consider a red spanning tree and blue spanning tree one at a time.
We can use disjoint-sets to merge connected components. Each component should be a tree, otherwise some grid edges will be enclosed inside some mirrors. So for the contracted graph, we would like to know how many spanning trees are there. This can be done by Kirchhoff’s theorem.
Since there are at most 200 broken mirrors, the number of vertices in the contracted graph should be no more than 401. Hence a O(|V|3) determinant calculation algorithm may be applied onto the matrix.










thanks for fast Editorial ;) And thanks for codes between text ;) ^ 2
Please, can i know what's wrong in my solution for 578B - "Or" Game ?
Run a second dp back to front (you can code this top down as well) and take the best of the two. (basically, your code calculates dp[i][K] as the best value among dp[i-1][k]|a[i-1][K-k] for all k<=K. Run the same code back to front, so you get the best dp[i][K] for dp[i+1][k]. Now take the best of the two).
Can you explain why do we need to run the second DP?
Hey, I've been thinking about this for a while and I honestly couldn't find a good reason that this works. I only tried it because I got hacked with 2 minutes remaining and I didn't have any better ideas. The last few test cases are all around 2-5 numbers each. Reverse dp takes care of the problem in this case, because the test case thrown up by @GyWXwshMy (where the optimal answer to a subproblem doesn't necessarily give the best answer overall) would only arise once. If you have a much larger array with this scenario arising many times, there is no reason to believe back to front dp will work. (Or at least I can't find any reason).
2 < 5 but (2 | 13) > (5 | 13), so you can't use DP to solve
I fail to find an error in my solution of F. Care to share full 52nd test?
Ok, got it, thanks a lot.
For the record, take all elements modulo P after building the matrix. If the prime is small enough, some checks of the kind
a[i][j] == 0fail ifa[i][j]is a multiple of P, and the Gauss method grieves and weeps.Don't you think that's a little bit bad that the precision issues affected the contestants so much?
For example, my C code:
Eps=1e-10 => Wrong Answer Eps=1e-11 => Accepted Eps=1e-12 => Time Limit Exceeded
I am surely not only one affected by those issues, is that really required for making a contest? I'm pretty sure that, if you've set checker to give wrong answer on >1e-6, no incorrect solution would pass.
I'd like a explanation of abovementioned constraint, maybe I'm missing something?
Thanks in advance.
Yea, same problem here, it would've been much nicer if they just required x as the output.
EDIT: Also just to be clear, the checker does check for an error up to 1e-6, but you probably do a binary search on x, and if you have an error on x of size 1e-6, this error gets added to all n values in you array, which means that the output (the weakness) may be off by a factor n * 1e-6. This is why you have to set your error term to 1e-6 / n or 1e-11.
But that still doesn't really justify asking for the weakness rather than x.
It helps a lot, thanks! I've been stuck for about half an hour for such a question.
I always use Pascal for this kind of tasks and it has never made mistake :)
Nice tasks, I feel bad that I slept.
Try to use iterative method. For example, you can run like 100 iterations of your search and it will get OK.
I ran 80 iterations and got WA
now, this is bad luck, I think:
http://codeforces.net/contest/578/submission/13030276
Maybe they should make this round unrated??? I got about -78 on this contest(My C with EPS=1e-8 had failed tests, but with EPS=1e-12 after contest it passed.)
Eventually, contest was interesting, but such problems create big problems :D
Its not bad luck. Its clearly mentioned that the relative or absolute error shouldn't exceed 10^-9. He must have used setprecision(10). The answer differs by 3e-9.
If you think it clearly said 10^-9 you should probably read the problem statement again.
Yeah, all of you are right, I made a mistake and I'm not trying to state that i was correct or anything, just trying to get a clarification on so tight precision required, because that clearly wasn't the main goal of the problem
And from now on, I'll be using iterative metjod, thanks :-)
Problem 3:
else printf("%.12f\n",(a+b)/(2.*((ab)/(2*b))));I think you lost '+' here. It must be
else printf("%.12f\n",(a+b)/(2.*((a+b)/(2*b))));, isn't it?Where is sorry_dreamoon?
I did the same thing for question OR GAME . But my answer generated wrong output . But when i ran same code on ideone / my machine , i got the correct answer same as jury output . I dont know where the fault is . Link of my ans:- http://codeforces.net/contest/579/submission/13050841 Wrong test case: 9
standart pow is evil, you should write your own function
Thanks.. It worked..
Your problem is in pow function, try to write it by your hand
I applied dp on DIV-2 D problem here is my solution can anyone explain why it failed ?
Dynamic programming solutions try to get the biggest answer by choosing the biggest answer on previous step, but hem can't work, because sometimes you should take not the biggest answer on previous step.
Example: (System test 23)
3 1 2
17 18 4
dp answers 53, but correct answer is 54Why?
let dp[i][j] = max OR of elements in range [0..i-1], and we can do up to j operations with element i. So here dp[2][0] = 53 ( 17 or (18*2) = 53 )
ans = dp[2][0] or a[2] = 53 or 4 = 53
But if we choose not the best answer on second position( (17*2) or 18 = 50), we can get
ans = 50 or a[2] = 50 or 4 = 54.
So dp can't work. If you have any issues, I'll be glad to help you.
Doesnt Ternary search take about logbase1.5(N) steps ? in C i looped 80 times and it gave WA and when i changed to 100 , it gave AC
http://codeforces.net/contest/578/submission/13051709
http://codeforces.net/contest/578/submission/13043558
Any idea why?
It's because precision of the answer should be at least 10-6. The higher the precision, the higher the number of iterations. You should set max number iteration is greater than 100.
You can also combine your 2 ternary searches.
Could somebody please explain the convex hull solution for div1 C more in detail? I don't get how you can find the answer using a geometry result.
Hi dreamoon_love_AA, can you please elaborate the convex-hull solution for div1 C, more importantly the upper and lower convex hull part with proof. Also, it would be great if you could share your thought process while coming up with this solution. Thanks.
Auto comment: topic has been updated by dreamoon_love_AA (previous revision, new revision, compare).
can someone point out misktake in my dp solution of div2 D problem... http://codeforces.net/contest/579/submission/13049193 thanx in advance...
Look here:
http://codeforces.net/blog/entry/20368?#comment-251505
I wonder how this code can help me to solve D div1!
Please, Can someone tell me why pow(5, 2) gave 24 instead of 25 on codeforces?? my solution of Div2 D
I'm not blue and i already know that codeforces community always say "be careful with using c++pow function".
I use Java but i think i've seen someone always say use ceil(pow(5,2)) instead
sorry I downvoted by mistake :P
I really don't care about upvotes. All i care about is getting better everyday till am red.
Use round for standart pow, or write your own pow func
That's about 2135646851368945132 time I see such question on CF.
I had the Div2 C correct just missed the last condition of x >= b. Stupid of me. Well, there goes my blue.
If you missed something in solution, it couldn't be correct. It's a fact!
For which reason has author posted such horrible code to problem Div1D?
Editorial must show how to solve problem, and code in it must be nice and clear. In this case we can see only stupid templates and not-formatted code with "nice" expressions like
Dou u really think it could be helpful for somebody?
Can someone explain the solution for div1D? I can't get the recurrence and I can't understand the code.
We consider the LCS dp table, if we know that lcs[n][n] = n-1, then the DP values lcs[x][y] which abs(x-y) > 1 are all useless, because they can never let lcs[n][n] get n-1. Now the useful states are lcs[x][y] which (x-y) <= 1, and their values would be min(x, y) or min(x,y)-1 , we can use them as states to do DP. F[i][3][2] denotes that the answer of first i characters , and the value of lcs[i][i-1/i/i+1] is min(i,i-1/i/i+1) or min(i,i-1/i/i+1)-1, that is 8 states that the solution mentions. So we can combine the transfer of LCS dp, to get the F.
Still don't get it. What is lcs[x][y]? LCS of input string with what? How use lcs table to get F table? Where is the answer?
lcs[x][y] denotes the LCS value of first x characters of T and first y characters of S, and now we enumerate the x-th character of T. Because lcs[x][y] = max(lcs[x-1][y], lcs[x][y-1], lcs[x-1][y-1]+1 if T[x]=S[y]), we can use this and their values to get the transfer of F. Above mentions, the F[n][1][1] denotes the number of T which can get the lcs[n][n]=n-1, i.e. the answer.
Thanks for explaining! The editorial and the code are so unclear and messy.
I'm sorry, but let's look to my two submissions in problem B div 1(1, 2). Why the fact that we can't take only the numbers with maximal bit don't repeal the improvement?
Because you think getting a new bit always better and your right but think about 15 and 16 multiplying by 3 they both can get 6. bit. I did the same mistake by the way.
You don't understand me. In text:
"If not, we can choose the largest number bj in sequence b, and change the strategy so that tj = k and all other tj = 0. The change will make the highest bit 1 of bj become higher so the or-ed result would be higher."
How we can associate it with test 32?
In these code, they choose the highest bit of a_i, not b_i.
Please think about what's the difference between them.
Thank you, I understood.
Can someone explain why in Div2 D.....DP from front and back passes and fails if we start from from front only.
Front only
Front and Back
I hope someone answers this
I think they are both wrong. 2 < 5 but (2 | 13) > (5 | 13) so you can't only get the best solution for prefix or suffix.
Weak test cases. Problem is not solvable by dynamic programming. ( At least the knapsack approach).
It was good time!!
Me too!
Can you explain the proof in the mirrors problem why a spanning tree on the red or blue nodes is necessary and sufficient? Basically I can see why it needs to be a spanning forest since any cycles in this graph would cause the second condition to be violated. However, why is a spanning tree the only way to satisfy the first condition?
It looks like if there are no cycles and both even and odd points do not form a spanning tree then at least two even boundary points are connected and at least two odd boundary points are connected, and from there it's obvious we can't pair all the boundary unit segments because of parity issues. The first fact looks obvious as well, but I don't see a simple proof.
A reasoning that may shed some light. Draw a curve as follows: start from some outer border segment, follow the path the ray takes (without actually touching the mirrors, just pass through the grid segments' centers) until the other border segment is reached, extend the curve to the next border segment (other than the one we used to enter) and so on until the line eventually loops. It follows from the statement that every segment in the grid is passed. Also, the grid points inside the curve are exactly the points of some fixed parity, and, further, they all must be connected. For every spanning tree there is exactly one way to connect all other points correctly.
I think there's a simpler solution to 1D without DP (the hard part is verifying that it's valid, I suppose, but this follows from a small bit of case analysis).
We want the number of strings other than S which can result from removing one character and adding one. First, we block the string S into groups of consecutive equal characters. Removing a character from any part of one group is equivalent, so if there are k groups, we consider each of these k possibilities. Suppose we've taken from a group with size g and character c; you can add back any color in any place, except you can't add back c adjacent to any of the g - 1 remaining c's in the group (or you would get S back). Also, for each other group with size h and color d, we overcount the number of ways to add another d into this group by h, so the total number of valid distinct ways to add a character to S with one of the k groups diminished is nm - n (since n is the sum of the sizes of all of the groups).
So our total answer would be k(mn - n), except a few of the strings T are double counted. It turns out that the only way to double count T is if there is some substring ab...aba in S (alternating different letters of some length ≥ 2) which becomes replaced by ba...bab (see if you can see the two ways to make this transformation). Thus the final answer is
which runs in O(n) pretty easily.
Code: 13057786
Nice! I have similar approach:
For each string T we can find the first position where S[i] != T[i] from both sides, let's say indices l and r. Consider the substring S[l:r+1] = ab..cd. Let's count such substrings of length one separately, i.e. we now consider length >= 2. It seems that T[l:r+1] can either be b..cdX or Yab..c. Since we want letters at positions l and r to be different, for the first case we have (a != b), (X != d), for the second (c != d), (Y != a). So if (a != b) we add (M — 1) possible values of X to answer, if (c != d) then we also add (M — 1). If both cases occured, we may have counted some cases twice: b..cdX = Yab..c. It follows that this may happen only if the substring is strictly alternating (ababa..., as in case of pi37) and if Y = sub[1] and X = sub[-2]. That means if string is alternating, we have counted only one case twice.
So we can count number of substrings with this properties (doable in O(n)) and compute the answer. Code: 13068410
pi37 I started out on the same path, but working on the second sample test case, I thought that since I am double counting, it must be wrong. Please tell me how did you notice that only alternating substrings give double counting? What gave you the idea?
Essentially, I just did a lot of casework. You don't want to see the details, but I was considering all possible strings R, R' such that you can remove something from S to get R,R', and add something to R, R' to get T, where S ≠ T, R ≠ R'. Then I considered the possible cases which could result in such an issue, which are:
1) Removing some character a and adding it back in in two different ways to get S → R → T and S → R' → T (it turns out this is impossible)
2) Removing some character a and adding in some character b in two different ways to get S → R → T and S → R' → T
3) Removing some character a and adding in a to get S → R → T, and removing some character b and adding in b to get S → R' → T.
With sufficient analysis of the possible relative positions of the removed and added characters, you eventually determine that alternating substrings are the only possible cases that give repetition.
If anyone has a better proof that these are the only bad possibilities, I would be interested to know.
Thanks for replying!
I hoped to become yellow but instead went blue, only because of precision issues. :/
I wanted to request you to add tag for editorial and announcement so that we can directly navigate from contest. Thanks.
DIV2 — problem C Can anyone explain why (a-b)/(2 * floor( (a-b)/2b ) ) is greater than (a+b)/(2 * floor( (a+b)/2b ) ) ?
dreamoon_love_AA can you prove this?
Damn, why do I always forget about this prefix/suffix sums. For Div1B I used sparse table (with OR instead of MAX) to compute OR of arr[:i] and arr[i+1:]. facepalm
I can't understand editorial for 579F - LCS Again ? Can someone help me ?
love cf <3
Div2 problem C — Can anyone explain me what "(a+b)/2*b" mean? Why can we divide by "2*b" ? Sorry, the tutorial was not clear to me :/
When c = a + b, can you find maximum y such that c / (2 * y) is not less than b?
can someone explain why my submission 13097889 passed ? after reading the editorial i think it's wrong to use dp here ... anyone have a case where the forward + backward dp fails ? and thnx :)
The number of ones in the binary representation can be found in O(k) time complexity, where k is the answer, instead of , which is in general slower: n & (n-1) == n without the last '1'. Like this: 13100947
, which is in general slower: n & (n-1) == n without the last '1'. Like this: 13100947
Doesn't matter when n is up to 109 only, but anyway :P
Can anyone explain to me that why c/2x must be an positive integer in Problem 3?
There are weak tests on Problem E:
Specifically, this part of the editorial is not true (EDIT: without modifying the sequences):
"Then you might guess that another direction of the induction is also true.That is, we can combine any k + 1 subsequence without backward steps into a whole sequence contains at most k backward steps. Your guess is correct !"
If, using the editorial's notation, A = 0 and D = 0 and B, C are positive, you cannot combine these subsequences. In other words, there only only subsequences of the form "RL...L" and "LR...R", these cannot be combined.
An example test that fails due to this is "RLLRRL". You can do this with one backward step with "3 5 6 1 2 4", but you can split it into "RL.R.L" and "..L.R.", which cannot be combined.
My practice submission (13541112) greedily found subsequences to combine by finding the longest one starting at the first remaining step until all were used. I had no proof of this, and while it got AC, it's wrong. For example, it only gives "3 5" on the above test.
Contest submissions that fail the above test include Egor's and subscriber's, both of which, interestingly, get RE due to specifically throwing an exception in this case. uwi, jcvb, snuke, yzyz, eddy1021, malcolm, and Vedensky all had contest submissions that WA/RE/TLE on this test as well.
Also, a request to fill in "Following provide one possible greedy method: The method will come soon...". How do you do it greedily correctly? I fixed my previous one by adding a special case (13548835) but I still have no proof that the initial idea of finding the longest subsequence repeatedly is correct. I suspect it is after the fix, but how do you prove it?
EDIT: I also should say that my purpose in making these posts is to let others know whether their solution may not be correct. I'm not blaming anyone, I know this kind of thing inevitably happens, but my goal in solving problems is not to get AC, but to have a correct solution, and I will try to fix any solution even AC if it isn't completely right. I try to help others with similar goals.
Firstly, Maybe you don't read the editorial carefully. How to combine "RL..R.L" and "L.R"?
You can get it from the editorial "Now we want to combine the final RL and LR subsequences together. We could pick the last footprint among two subsequences, exclude it from the original subsequcne and append it at the tail of another subsequence. The move will not increase the number of backward step and the types of the two subsequences would become RR and LL !".
Secondly, how do we greedily it correctly? Because I'm a very very very lazy man.... So I still don't explain it. (I think it's just a dirty work and there are many possible greedily method.). But it seem there are still people want to know it. I will edit it after some hours...
Thirdly, I also feel the testdata is very work, it's my fault. I originally think the random testcases are enough to catch wrong method. But I'm wrong. It's a very sad thing for me about the contest. I am too weak such that I cannot generate enough good testcase before contest. Q_Q
Ah okay yeah I missed that part, my bad. That's the same fix I thought of.
Looking forward to a proved method for the greedy :). Thanks for the interesting problem and contest!
Auto comment: topic has been updated by dreamoon_love_AA (previous revision, new revision, compare).
The problem D is very similar to this one.
I understand why we need to find maximum y(integer) problem c. but, I can't understand why y equal floor((a+b)/(2*b)) Somebody can explain why?? help!!
In Div 1 C given A and B are decreasing and increasing functions can someone explain how does applying binary search help us in getting the corresponding x that gives us max value. Thanks :)
In Div2 C 578A - A Problem about Polyline, could someone explain this line of editorials " In fact, (a-b)/(2(a-b)/2b) always dosn't exist or larger than (a+b)/(2(a+b)/2b) " how to proof this?!
In the binary search solution of weakness and poorness,why is there a loop from 0 to 100 i.e why binary search is done only 100 times.What is its significance?
Has somebody solved the Problem 5 Weakness and Poorness using Ternary Search? I tried solving it using a ternary search but am getting a precision error in my code. I tried to decrease the error by increasing the limit of ternary search more but then I got TLE which is obvious as increasing the search space would make the program run for a longer duration. Here is my submission link to both the parts 1) Wrong Answer on Test Case 26: 82399517 2) TLE on Test Case 4: 82399713
If somebody could tell me how to deal with such precision errors, it would really help. I have never dealt with errors like these before.
Thanks in advance.
Weak tests on problem F
Should output $$$0$$$ but a number of accepted submissions output $$$1$$$
Can anyone help me by explaining why are we iterating 100 times rather than using normal binary search in problem 5 : Weakness and Poorness[problem:578C].Thanks!
To avoid infinity loop I guess, especially when dealing with real numbers.
you actually replied to a comment from 3 years ago xD
I knew it XD