COCI2015_task ACM - Codeforces

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	165
2	maomao90	164
3	Um_nik	163
4	atcoder_official	160
4	adamant	160
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
8	Dominater069	154
8	nor	154

Hi CF. help me please :)

problems at COCI2015. TASK ACM

The team of the University of Zagreb – Stjepan, Ivan and Gustav – are taking part in the World Finals of the ACM International Collegiate Programming Contest in Morocco. Their technical guide Goran has come up with an invincible strategy to use for solving tasks in the finals. In the very beginning, each team member quickly estimates the difficulty of each of the N tasks. The difficulties are described by numbers from 1 to 5, and their meaning is the following:

• 1 hehehe • 2 bring it on! • 3 well OK. • 4 hmmmm. . . • 5 are you insane?

After this, they will distribute the tasks between them. For simplicity’s sake, the array of tasks will be split into three parts so that each team member gets a nonempty array of consecutive tasks to contemplate about. The distribution is made so that the sum of estimated difficulties is minimal, whereas only the estimate of the team member whom that task is assigned to is calculated. Your task is to calculate that minimal possible sum.

INPUT

The first line of input contains the integer N (3 6 N 6 150 000), the number of tasks. Each of the following three lines contains N integers (from 1 to 5): the estimated task difficulties, given respectively. First of those lines corresponds to Stjepan’s estimates, the second to Ivan’s and the third to Gustav’s.

OUTPUT

The first and only line of output must contain the minimal sum of difficulties.

SAMPLE TESTS

input

1 3 3

1 1 1

1 2 3

output 4

input

3 3 4 1 3 4 4

4 2 5 1 5 5 4

5 5 1 3 4 4 4

output 19

Clarification of the first example: Stjepan gets the first, Gustav the second, and Ivan the third task.

Комментарии (8)

Показать архивные | Написать комментарий?

robinyu

9 лет назад, # |

← Rev. 2 →

Let's say we want Stjepan to get contiguous segment from 1 to a - 1, Ivan segment a to b - 1, and Gustav–segment b to N. So, we will simplify the problem. Let's call Stjepan's difficulties A₁, A₂, ..., A_N, Ivan's difficulties B₁, B₂, ..., B_N, and Gustav's difficulties C₁, C₂, ..., C_N.

Let's define the function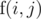 $\text{[math]}$ , to be the minimum total sum of difficulty to solve up to the 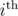$\text{[math]}$ problem, using up to the 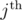$\text{[math]}$ person. Of course, if i = 0, then there are no problems to solve so the answer is 0.

What's the minimum sum of difficulty of solving up to problem i, if only Stjepan can solve problems? Obviously, answer is A₁ + A₂ + ... + A_i. In other words,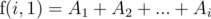 $\text{[math]}$ .

Now, what's the minimum sum of difficulty solving up to problem i, if only Stjepan and Ivan can solve problems? We can assign problem i to Stjepan, then the answer will be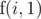 $\text{[math]}$ (since if we give this problem to Stjepan, we have to give all problems 1 to i to him in order to satisfy the original constraint that he will get the contiguous segment starting from 1), or we can assign the problem to Ivan, in which case answer will be 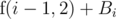$\text{[math]}$ . Obviously we want to minimize the total sum, so we pick the smaller of the two. In other words, $\text{[math]}$ .

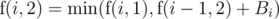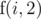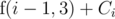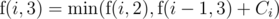What's the minimum sum of difficulty solving up to problem i, if Stjepan, Ivan and Gustav can solve problems? It's quite similar to the previous one. We can assign problem i to either Stjepan or Ivan, then the total difficulty will be $\text{[math]}$ or we can assign problem i to Gustav, then the total difficulty will be $\text{[math]}$ . So, $\text{[math]}$ . If we implemented it correctly (store the previous answers using DP), then it should run in O(3N) = O(N).

In this simplified problem, the answer is simply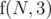 $\text{[math]}$ . Unfortunately, we kind of cheated, since it's not guaranteed that Stjepan will get 1 to a - 1, Ivan a to b - 1, and Gustav b to N. In fact, maybe Ivan will get problems 1 to a - 1, or maybe Gustav will get problems 1 to a - 1. But it doesn't really matter. There are only 3! = 6 different permutations of the three people, so just check all permutations of roles. In other words, we should try: