581A — Vasya the Hipster
The first number in answer (number of days which Vasya can dress fashionably) is min(a, b) because every from this day he will dress one red sock and one blue sock.
After this Vasya will have either only red socks or only blue socks or socks do not remain at all. Because of that the second number in answer is max((a - min(a, b)) / 2, (b - min(a, b)) / 2).
Asymptotic behavior of this solution — O(1).
581B — Luxurious Houses
This problem can be solved in the following way. Let's iterate on given array from the right to the left and will store in variable maxH the maximal height if house which we have already considered.Then the answer to house number i is number max(0, maxH + 1 - hi), where hi number of floors in house number i.
Asymptotic behavior of this solution — O(n), where n — number of houses.
581C — Developing Skills
This problem can be solved in many ways. Let's consider the most intuitive way that fits in the given time.
In the beginning we need to sort given array in the following way — from two numbers to the left should be the number to which must be added fewer units of improvements to make it a multiple of 10. You must add at least one unit of energy to every of this numbers. For example, if given array is {45, 30, 87, 26} after the sort the array must be equal to {87, 26, 45, 30}.
Now we iterate on the sorted array for i from 1 to n. Let's cur = 10 - (aimod10). If cur ≤ k assign ai = ai + cur and from k subtract cur else if cur > k break from cycle.
The next step is to iterate on array in the same way.
Now we need only to calculate answer ans — we iterate on array for i from 1 to n and assign ans = ans + (ai / 10).
Asymptotic behavior of this solution — O(n * log(n)) where n is the number of hero skills.
581D — Three Logos
This problem can be solved in many ways, let's consider one of them.
The first step is to calculate sum of squares s of given rectangles. Then the side of a answer square is sqrt(s). If sqrt(s) is not integer print -1. Else we need to make the following.
We brute the order in which we will add given rectangles in the answer square (we can do it with help of next_permutation()) and for every order we brute will we rotate current rectangle on 90 degrees or not (we can do it with help of bit masks). In the beginning on every iteration the answer square c in which we add the rectangles is empty.
For every rectangle, which we add to the answer square we make the following — we need to find the uppermost and leftmost empty cell free in answer square c (recall that we also brute will we rotate the current rectangle on 90 degrees or not). Now we try to impose current rectangle in the answer square c and the top left corner must coinside with the cell free. If current rectangle fully placed in the answer square c and does not intersect with the some rectangle which has already been added, we need to fill by the required letter appropriate cells in the answer square c.
If no one of the conditions did not disrupted after we added all three rectangles and all answer square c is fully filled by letters we found answer and we neeed only to print the answer square c.
Else if we did not find answer after all iterations on the rectangles — print -1.
For random number of the rectangles k asymptotic behavior — O(k! * 2k * s) where s — the sum of squares of the given rectangles.
Also this problem with 3 rectangles can be solved with the analysis of the cases with asymptotic O(s) where s — the sum of squares of given rectangles.
581E — Kojiro and Furrari
Let's f — the position of start, and e — the position of finish. For convenience of implementation we add the gas-station in point e with type equals to 3.
Note: there is never a sense go to the left of the starting point because we already stand with a full tank of the besr petrol. It is correct for every gas-station in which we can appear (if in optimal answer we must go to the left in some gas-station pv, why not throw out all the way from pv to current gas-station v and back and after that the answer will be better). Now let's say about algorithm when we are in some gas-station v.
The first case: on distance no more than s there is the gas-station with quality of gasoline not worse, than in the current gas-station. Now we fix nearest from them nv (nearest to the right because go to the left as we understand makes no sense). In that case we refuel in such a way to can reach nv and go to nv.
The second case: from the current gas-station we can reach only gas-station with the worst quality (the type of the current gas-station can be 2 or 3). If we are in the gas-station of type 2 we need to refuel on maximum possiblevalue and go in the last achievable gas-station. If we are in the gas-station with type 3, we need to go in the farthest gas-station with type 2, but if there is not such gas-station we need to go to the farthest gas-station with type 1. This reasoning are correct because we first need to minimze the count of fuel with type 1, and the second to minimize the count of fuel with type 2.
This basic reasoning necessary to solve the problem. The next step — calc dynamic on all suffixes i of gas-stations — the answer to the problem if we start from the gas-station i with empty tank. We need to make updates, considering the above cases. For update the dynamic in v we need to take the value of dynamic in nv and make update in addiction of the case. If the case is equals to 1, we need to add to appropriate value the distance d from v to nv. If this case is equals to 2 and we are in the gas-station with type equals to 2 we need to add s to the second value of answer, and from the first value we need to substract s–d. If it is the case number 2 and we are in the gas-station with type equals to 3, we need to substract from the value, which determined by the type of the gas-station nv, s–d.
Now to answer on specific query of the starting position we nned to find the first gas-station which is to the right of the startiong position, make one update and take the value of dynamic, which already calculated, and recalculate this value in accordance with the above.
Asymptotic behavior — O(n logn) or O(n) in case how we find position in the list of gas-stations (the first in case of binary search, the second in case of two pointers).
To this solution we need O(n) memory.
581F — Zublicanes and Mumocrates
Let the number of leavs in tree (vertices with degree 1) is equal to c. It said in statement that c is even. If in given graph only 2 vertices the answer is equal to 1. Else we have vertex in graph which do not a leaf — we hang the three on this vertex.
Now we need to count 2 dynamics. The first z1[v][cnt][col] — the least amount of colored edges in the subtree rooted at the vertex v, if vertex v already painted in color col (col equals to 0 or to 1), and among the top of the leaves of the subtree v must be exactly cnt vertices with color 0. If we are in the leaf, it is easy to count this value. If we are not in the leaf — we count value with help of dynamic z1[v][cnt][col]: = z2[s][cnt][col], where s — the first child int the adjacency list of vertex v.
We need the second dynamic z2[s][cnt][col] to spread cnt leaves with color 0 among subtrees of childs of vertex v. To calc z2[s][cnt][col] we brute the color of child s — ncol and the number of childs i with color 0, which will be locate in subtree of vertex s and calc the value in the following way — z2[s][cnt][col] = min(z2[s][cnt][col], z2[ns][cnt–a][col] + z1[s][a][ncol] + (ncol! = col)), where ns — the next child of vertex v after the child s. Note, that it is senselessly to take a more than the number of leaves in the subtree s and to take more than the number of vertices in subtree — sizes (because in that case it will not be enough leaves for painting).
The upper bound of asymptotic for such dynamics O(n3). We show that in fact it works with asymptotic O(n2). Let's count the number of updates: 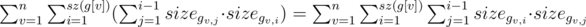 . Note, that every pair of vertices (x, y) appears in the last sum (x, y) exactly once when v = lca(x, y). So we have no more than O(n2) updates.
. Note, that every pair of vertices (x, y) appears in the last sum (x, y) exactly once when v = lca(x, y). So we have no more than O(n2) updates.
Asymptotic behavior of this solution: O(n2).











Thank you for fast editorial
Wow you certainly came prepared with this! :) Thanks!
Such a fast system testing, thank you :D
For problem C it's easy to derive a O(n) solution if we consider sorting the numbers with a radix/bucket sort, as we only need to check the last digit.
C have solution O(n) 13267229
O(S) solution for problem D : https://ideone.com/HomOtB
Problems were very interesting. so good... thanks for making this contest!!!
What is test #5? Author, could you kindly share this test somewhere? It looks like random test, but my solution fails on it. (It seems it works fine for all small tests from your test set).
Can someone please explain the solution to F in more detail: I do not get how we are calculating z2[s][cnt][col] using information from the next child of s. How can we use a value in the DP table that is being computed in the same "level". As in won't z2[ns][ * ][ * ] be uncomputed when we are trying to calculate z2[s][cnt][col]?
You can calculate DP from the right to the left, from last child to the first. Also you can use "lazy DP" — if needed value is not calculated — calculate it recursively. Else just take calculated value.
I have a 20 line brute force solution for D that passed during contest which you may like: http://codeforces.net/contest/581/submission/13283931
Wow, very interesting solution. Congratulations on such a large rating increase ;)
This was a really interesting contest! Thanks for it :)
I have a question regarding the solution's time complexity for problem F, though, and if anybody could explain it in intuitive terms, I would be much obliged! (I don't really understand the last summation, I only understand that the first summation is 'for each node v', and the second summation is 'for each child i of node v')
Can somebody explain to me how works the DP solution of problem F? I didn't understand very well :/
PS: Very interesting contest :)
The overall idea of the dp is to try to color (starting from the root node) each node either 0 or 1, and to find the minimum number of 'bad' edges — edges which connect nodes of 2 different colors — within the subtree of that node, at the same time asserting that there must be a certain number of leaf nodes colored one color (in the editorial's case, 0).
The dp introduced in the editorial is termed like such: z1[v][cnt][col] (the first dp) which is the minimum number of bad edges in the subtree of v when v has col (0/1) for its color, and exactly cnt # of leaves in subtree of v are colored 0. So, the answer for the entire problem is min(z[root of tree][number of leaves / 2][0], z[root of tree][number of leaves / 2][1]).
Make sure you understand everything above before proceeding on because otherwise it might be difficult to understand the 2nd dp introduced in the editorial.
Now, how do you transition from z1[v][cnt][col] to another state? I.e. you have colored node v with color col, and you need to color cnt # of leaves with color 0. How do you proceed to color the nodes in the subtree to satisfy all these conditions? When you are z1[v][cnt][col], you have a list of children — call it C — of node v (say size m). You can color each of the children in C 0/1, but there is one condition that you must satisfy; for the transitions to the children in C, i.e. z1[C1][cnt1][0/1], z1[C2][cnt2][0/1], ..., z1[Cm][cntm][0/1], you must ensure that cnt1 + cnt2 + ... + cntm = cnt. You do this with the 2nd dp, that is a knapsack-style dp.
Now for the 2nd dp, it is termed like such: z2[s][cnt][col]. This one is complicated, so let me define some terms. p = parent of s. Define 'suffix subtree' of s to be the subtree of p excluding all the subtrees of the children of p which come before s in the child list of p and the edges that connect them to p. E.g. for a simple tree rooted at node 1, and 1 has children in its list C as 2, 3, 4, 5, in this order, then the 'suffix subtree' of node 3 will be the subtree of its parent, 1, excluding the subtree of 2 (because 2 is a child of 1 that comes in the list of children before 3) and the edge 1-2.
Now, with the terms above defined (and hopefully understood — especially the important idea of 'suffix subtree'), z2[s][cnt][col] is the minimum number of bad edges in the 'suffix subtree' of node s such that cnt # of leaves in the 'suffix subtree' are colored 0, and col is the color of parent p.
At this point, you should be able to understand why the transition for the first dp z1[v][cnt][col] is just the 2nd dp z2[s][cnt][col], where s is the first child of v.
Ok, so we have completely solved the first dp at this point, yay!
Finally, to finish off, we need to be able to solve the 2nd dp. How do we transit from z2[s][cnt][col]? Well, we know that we have to color s either 0/1, so try both colors (i.e. z1[s][ ][0] and z1[s][ ][1]) and take the minimum. So how do we know how many leaves in subtree of s we should color (I left blanks on purpose in above 'z1[s][ ][0] and z1[s][ ][1]')? Actually, we don't know. So, try all possibilities, i.e. z1[s][0...min(#leaves in subtree s, cnt)][0/1]. After putting i leaves in the subtree rooted at s, we have cnt-i leaves left to color, which we leave as a job for z2[ns][cnt-i][col], where ns is the child that comes directly after s in the list of children of p.
Hence the formula: (trying i from 0...min(#leaves in subtree s, cnt), and trying each color 0/1, called ncol) z2[s][cnt][col] = min(z1[s][i][ncol] + (ncol != col) + z2[ns][cnt-i][col]). Note that (ncol != col) is necessary because when the node s is colored differently from the parent node p, then p-s is a bad edge.
I have left out the base cases because I think you can figure that out yourself easily after you've understood the main bulk of the dp idea!
Hope I managed to help; I was quite confused at first, too! :)
Thanks for the brilliant explanation. Can you also explain why the dp is asymptotically order n^2 ?
Unfortunately I am still not able to understand the analysis in the editorial that proves it to be O(n^2) :(
...
One funny thing on F:
Even though the editorial specifically mentions the special case n=2:
"If in given graph only 2 vertices the answer is equal to 1"
there is no case with n=2 in the test data. You can be sure that quite a few wrong solutions pass in this way :P
Also just to add one thing:
You can do F with only one dp and without the extra parameter {0,1}. Think of it as coloring each node white or black. Then, can[x][j] is the minimum number of bad edges using the subtree of vertex x with exactly j dead zones colored black, where vertex x is colored white (almost...).
To do transitions we iterate over the children of vertex x and do it knapsack-style. In this setup, the number of bad edges is exactly the number of times we take a subtree rooted at a black node, which according to our earlier setup never happens (oops).
The fix here is to notice that we can flip an entire subtree, making the root black and inverting the colors of each dead ends within, so after calculating can[x], we apply the transitions can[x][s[x]-i]=min(can[x][s[x]-i],can[x][i]+1), where s[x] is the number of dead ends in x's subtree.
DO NOT see 13290307 for an implementation.
EDIT:
OK another weak thing about tests: O(n^3) solution without exploiting the property making it O(n^2) passes, for example my linked submission above. A countertest (like a long chain with a high-degree vertex at the end) is
Two fixes here:
Keep track of which values in cnt[x] are already filled in to be used, which reduces the complexity as desired, such as in 13291603.
Add size as you go (s[x] only includes already-processed children) — 13291744.
EDIT 2: Okay oops I'm dumb replace 5000 with 4999
F: where s — the first child int the adjacency list of vertex v. in ? :)
Here's my implementation to D problem. The same algorithm can be used to solve the problem with arbitrary k triangles. I hope this helps.
Can you share your code for problem E, for better understanding the idea ?
Thanks for the nice contest and solutions!
Here is an alternate solution to E, which I think allows queries of pairs (f_i, e_i) rather than just f_i.
Let's think about the problem in this equivalent way:
We have a number line and several segments of length s labelled with 1, 2, or 3. We have queries of the form (f_i, e_i), meaning we want to go from f_i to e_i minimizing the time spent on first segments labelled 1, then segments labelled 2. We also begin with a free segment labelled 3 at f_i.
Here is how we answer one query:
First let f_i = f_i+s. The purpose of the free segment is to ensure it isn't better to first go backwards, but it's probably manageable without this restriction as well.
1: We check if it's possible at all — check if the entire length of the line between the two points is covered by some segment. If it isn't possible return (-1, -1), since there is some point we cannot pass.
2: If it is possible, we check how long we must spend on segments labelled 1. Convince yourself that this is simply the distance between the two points minus the length covered by only segments labelled 2 and 3.
3: We check how long we must spend on segments labelled 2. By similar reasoning, this is equal to the entire distance minus the length covered by segments labelled 3, minus the answer found in step 2.
To implement this for problem E, we use coordinate compression and prefix sums for what is covered by each set of numbers used above ({1,2,3}, {2,3}, {3}). The span between the query and the first compressed point must be dealt with as a special case.
Overall, it is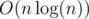 time (which can be made O(n) after sorting with two pointers) and O(n) memory. Here is my implementation: 13309041.
time (which can be made O(n) after sorting with two pointers) and O(n) memory. Here is my implementation: 13309041.
EDIT: You can also remove the special case by doing it offline: 13309187.
Hello :),
Did anyone implemented problem F according to the editorial?
I didn't understand the complexity analysis of the problem F.
Can someone explain it in detail?
.
.