Opencup: GP of Japan

9 лет назад, # ^ |

← Rev. 2 →

+20

Если gcd(n, f(n))! = 1, то -1. Иначе,находим минимальное число m, такое что a^m + 1 = a(mod n). Тогда n^k - 1 должно делиться на m. И находим минимальное такое k. Это и будет ответ. UPD В 46 тесте кажется что-то вроде N=51,ответ должен быть 4.

→ Ответить

9 лет назад, # ^ |

Как именно эти числа m и k найти-то? Тупо перебором, что ли?

→ Ответить

Temirulan

9 лет назад, # ^ |

← Rev. 2 →

Видимо если n^k = 1(modm) то k является делителем phi(m). phi(m) — функция Эйлера.

→ Ответить

9 лет назад, # ^ |

← Rev. 2 →

Как в таком случае m найти?

a у нас лежит в границах 0..n - 1, как его перебрать?

→ Ответить

9 лет назад, # ^ |

← Rev. 2 →

+10

Заметим,что m — делитель f(n). Дальше я находил так, перебирал все делители f(n), и проверял выполняется ли равенство a^m + 1 = a(mod n) для всех чисел от 1 до 1000.И если для всех выполняется, то такой m -подходит. Сразу скажу,что не умею доказывать это, и даже не знаю верно ли это.

→ Ответить

Kaban-5

9 лет назад, # ^ |

← Rev. 5 →

+39

Функция Кармайкла (минимальное такое m > 0, что для любого a, взаимно простого с n, верно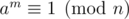 $\text{[math]}$ , обозначается λ(n)), равна НОК функций Кармайкла для простых степеней, входящих в n. Для простых степеней s (за исключением 4, 8, 16, ..., для которых она равна 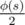$\text{[math]}$ ) она равна φ(s).

Но мы хотим, чтобы для всех a выполнялось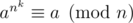 $\text{[math]}$ . При бесквадратных n достаточно выполнимости этого для a, взаимно простых c n. Тогда нужно 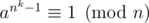$\text{[math]}$ для всех a, взаимно простых c n. Тогда легко получить, что n^k - 1 делится на λ(n), откуда в качестве k достаточно перебирать делители φ(λ(n)).

→ Ответить

9 лет назад, # ^ |

Непонятно тогда, зачем ставить тайм-литим 4 секунды, если общая ассимптотика (O(sqrt(N)))

→ Ответить

Kaban-5

9 лет назад, # ^ |

Ну да, наше решение работает мгновенно. Может быть авторы хотели, чтобы можно было что-то попроще написать, например явно перебирать k?.

→ Ответить

TigranHakobyan

9 лет назад, # ^ |

+13

явно перебирать не получилось TLE54.

→ Ответить

TigranHakobyan

9 лет назад, # ^ |

а почему это так ?

→ Ответить

perec1970

9 лет назад, # |

Скажите, как решать задачу А (о префектурах) и задачу G (о площади поверхности) из див.2 Спасибо.

→ Ответить

ultizet

9 лет назад, # ^ |

A: просто переберём границу. Для границы между 0 и 1 суммой ошибок будет количество W во входных данных. Теперь научимся переходить от границы между i и i + 1 к границе между i + 1 и i + 2. Поймём, что это означает переход префектуры i + 1 из восточной части в западную, поэтому из ошибок надо вычесть количество W и добавить количество E в столбце i + 1 входных данных (в 1-индексации). Для всех вариантов границы найдём тот, который даёт минимум ошибок

→ Ответить

perec1970

9 лет назад, # ^ |

Если можете, скиньте Ваш код. Спасибо.

→ Ответить

ultizet

9 лет назад, # ^ |

Код

→ Ответить

Temirulan

9 лет назад, # ^ |

Изначально имеем площадь 2 * (a * b + a * c + b * c). Каждый раз когда удаляем кубик считаем сколько сторон его входят в ответ(x) и сколько не входят(y). Ответ меняется на + y - x. code

→ Ответить

perec1970

9 лет назад, # ^ |

Скажите, а что делает эта строка в Вашей программе (return removed.count(mp(mp(x, y), z));) Я так понимаю что возвращает сколько в mape чисел. А как у Вас описано mp. Если Вас не затруднит, то скиньте описание всех Ваших переменных. Спасибо.

→ Ответить

MrDindows

9 лет назад, # ^ |

std::make_pair

→ Ответить

pkhaustov

9 лет назад, # |

Мне бы еще хотя бы условие задачи J кто-нибудь рассказал. Чему верить, текстовому описанию или двунаправленной стрелочке? За 30 минут до конца я все-таки решил послать клар, но на него никто не ответил.

→ Ответить

9 лет назад, # ^ |

Скорее стрелочке. У нас по тексту был WA15, а по стрелочке — TL26.

→ Ответить

pkhaustov

9 лет назад, # ^ |

А у меня и по стрелочке WA15. Есть отличие в чем-нибудь кроме того, как рассматривать людей с равным вкладом?

→ Ответить

permin

9 лет назад, # ^ |

я верил стрелочке -- OK

→ Ответить

Furko

9 лет назад, # |

Как решать I?

→ Ответить

9 лет назад, # ^ |

← Rev. 2 →

Вариация на тему convex hull trick #2. Уже 2ой opencup подряд задача на трюк из этого списка.

(Upd. забыл важную деталь — решение надо писать на C++, на Java оно не лезет в ТЛ; на плюсах впрочем лезет менее чем с 2x запасом, что наводит на мысль, что у жюри есть что-то в константу раз быстрее)

→ Ответить

ivan.popelyshev

9 лет назад, # ^ |

Если использовать ArrayList-ы и давать convex hull-у удалять дальше текущего начала списка, то она заходит, на тест уходит примерно ~30Мб памяти вместо 200. Почему джава не любит когда мы используем много памяти — а хрен его знает.

→ Ответить

danilka.pro

9 лет назад, # ^ |

Я постарался максимально аккуратно написать все то же решение — зашло за 428ms.

→ Ответить

9 лет назад, # |

H: надо дополнить граф до эйлерова так, чтобы сумма весов была минимальна. Несложно заметить, что это эквивалентно тому, чтобы найти min cost паросочитание на концах данных отрезков. Т.к. отрезки ориентированные, граф к счастью получается двудольным.

→ Ответить

akim

9 лет назад, # ^ |

Можно подробнее про решение? Как учесть пересечения отрезков? Иногда нужно делить отрезки на два в точке их пересечения, чтобы улучшить ответ. Если же мы будем учитывать все пересечения, то количество отрезков может увеличиться до n² и min cost паросочетание не зайдет по времени.

→ Ответить

9 лет назад, # ^ |

← Rev. 2 →

Зачем их учитывать? У пересечений deg_in = deg_out, а для дополнения до Эйлерова графа нас интересуют только вершины с дисбалансом (т.е. все концы — если какие-то концы совпадают, просто считаем их несколько раз).

→ Ответить

akim

9 лет назад, # ^ |

Спасибо, теперь все понятно.

→ Ответить

lessmeaning

5 лет назад, # ^ |

А эту задачу можно решить если нет условия связности, то есть в условии не было бы дано что граф изначально связан (если убрать направления ребер)?

→ Ответить

9 лет назад, # |

J: сначала надо понять, что имеется в виду эквивалентность, а не следствие (иначе WA 15). Потом строим ориентированный граф: для прямых условий типа "<" добавляем дугу как есть, для условий на соседях типа "<" сортируем соседей, разбиваем на классы одинаковых, и между классами добавляем линейное число дуг при помощи фиктивных вершин (т.е. если класс v₁, ... v_k меньше класса w₁, ..., w_l, добавляем новую вершину x и дуги v_i -> x и x -> w_j.

Для условий типа "=" просто добавляем их в disjoint sets union и стягивае компоненты в графе. В итоговом графе жадным проходом считаем ответ.

→ Ответить

I_love_Tanya_Romanova

9 лет назад, # ^ |

Заходит попроще.

Будем рассматривать вершины в порядке увеличения продуктивности, и поддерживать для каждой вершины параметр "у ее новых соседей продуктивность должна быть не ниже Х". Если у всех вершин разные продуктивности, то уже вроде должна работать обычная жадность — берем очередную вершину, ставим ей максимум из ограничений по ее соседям, пересчитываем ограничения по ее соседям.

Пока что это получит ВА15, потому что у нас могут оказаться две вершины с одинаковой продуктивностью, которые знают друг о друге, но которым мы дали разные зарплаты — а стрелочка в условии в обе стороны.

Чтобы это пофиксить, будем добавлять вершины с одинаковой продуктивностью группами, и после каждого добавления жадно исправлять все противоречия, пока они есть (т.е. если у нас есть пара вершин с одинаковой продуктивностью, из которых одна знает о другой, то поднимем зарплату той, у которой она меньше). Код — link.

→ Ответить

9 лет назад, # ^ |

А как быстро определять компоненты в группах равных?

→ Ответить

9 лет назад, # ^ |

М, что за компоненты? Мы просто делаем то же самое, что и с условиями типа "<", только вместо графа используем DSU. Т.е. если есть ребро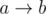 $\text{[math]}$ и c_a = c_b, то делаем dsu.unite(a, b). То же самое с условием типа "=" на соседях: если c_v₁ = ... = c_{v_k}, то объединяем v₁, ..., v_k в DSU. Потом просто стягиваем компоненты из DSU в орграфе для условий "<".

→ Ответить

9 лет назад, # ^ |

Как мы определяем, что из группы с чем объединять?

→ Ответить

9 лет назад, # ^ |

Всё со всем. Ну т.е. v₁ с v₂, ..., v_k, или v_i с v_i + 1, или что-нибудь ещё, для DSU не важно. Или я неправильно понимаю вопрос?

→ Ответить

9 лет назад, # ^ |

Я правильно понимаю, что тогда всегда у группы одинаковых зарплата будет одна и та же?

→ Ответить

9 лет назад, # ^ |

Да, у группы одинаковых, обединённой таким образом (т.е. группы одинаковых соседей или пары одинаковых напрямую вершин), ответ один и тот же.

→ Ответить

Fcdkbear

9 лет назад, # ^ |

← Rev. 3 →

Можно тоже самое, только без фиктивных вершин.

Отсортируем для каждой вершины все исходящие ребра по продуктивности. Теперь первым проходом обьеденим все вершины, которые нужно обьединить. Потом аналогичным проходом попроводим ребра такие же как вы сказали, только в другом направлении (от вершины с большей продуктивностью к меньшей в сжатом графе).

Получили DAG. В этом DAG для каждой вершины посчитаем максимальное расстояние, на которое можно из нее уйти (для листа считаем, что оно равно 1) — это простая динамика. Легко заметить, что вот эта величина как раз и равна зарплате всей компоненты, которую представляет эта вершина DAG

→ Ответить

9 лет назад, # ^ |

Good point. Фиктивные вершины нужны только в понимании условия "как написано", а не "как в формулах". В правильном понимании можно и напрямую соединять.

→ Ответить

9 лет назад, # ^ |

А как жадно считать ответ? Брать вершины в порядке возрастания производительности?

→ Ответить

permin

9 лет назад, # ^ |

Число в вершине это длина самого длинного пути, ведущего в эту вершину в полученном DAG.

→ Ответить

9 лет назад, # |

Как решать E?

→ Ответить

9 лет назад, # ^ |

+16

Нам нужно фактически решить задачу "для каждой точки определить, попадает ли она во внешнюю грань планарного графа". Сначала для простоты выкинем все мосты из графа, так как они практически не влияют на структуру граней. Применим к картинке случайное аффинное преобразование, чтобы в графе не осталось вертикальных отрезков.

Выделим "внешние" грани. Почему внешние в кавычках — потому что трудно понять, что грань (т. е. последовательность рёбер в порядке их обхода) является действительно внешней, так как она может содержаться внутри какого-то большего многоугольника. Поэтому будем называть "внешней" гранью любую последовательность рёбер, являющуюся границей грани, такую, что ориентированная площадь образованного ими многоугольника (возможно, у многоугольника будут самокасания по вершине, но это не страшно) отрицательна.

Теперь будем идти сканирующей прямой, поддерживая все рёбра, пересекающие данную прямую в декартовом дереве. Каждое ребро будет либо открывающимся, либо закрывающимся. Тогда чтобы проверить точку, надо посчитать баланс в этой точке — если он положительный, то точка внутри.

→ Ответить

9 лет назад, # ^ |

Ага, понятно. Мы (почти) такое же придумали, но я решил что вряд ли такое кто-то на контесте будет писать. Недооценил другие команды, вы молодцы!

→ Ответить

9 лет назад, # ^ |

И как такое писать за разумное время? :) Было бы интересно увидеть код.

→ Ответить

9 лет назад, # ^ |

+24

Наш код: http://pastebin.com/U2c1RSN9

→ Ответить

9 лет назад, # ^ |

Проще чем я ожидал. Спасибо!

→ Ответить

Zhukov_Dmitry

9 лет назад, # ^ |

А ещё это можно с обычным set'ом написать, если вместо сумм хранить направление отрезка (x1 < x2 или x1 > x2, сканирующая прямая вдоль OX двигается) при обходе многоугольников против часовой стрелки. Тогда, зная ближайший отрезок выше данной точки, можно по его направлению понять, внутри мы или нет.

Только в этом решении нельзя забывать о том, что одни многоугольники могут быть внутри других. То есть, если при добавлении очередного отрезка мы понимаем, что находимся внутри какого-то многоугольника, то просто не добавляем его. Либо добавляем, но запоминаем, внутри кого мы. Но в этом случае, если мы определили, что мы не внутри того многоугольника, отрезок которого нашёлся над проверяемой точкой, то мы внутри того многоугольника, внутри которого лежит этот отрезок.

→ Ответить

adamant

9 лет назад, # ^ |

+16

Глядя на это, я понимаю, что когда-нибудь наступит день, когда в теоретический минимум спортивного программиста будет входить диаграмма Вороного :)

→ Ответить

qwerty787788

9 лет назад, # ^ |

А она еще не входит? :(

→ Ответить

9 лет назад, # ^ |

У нас такое же решение, но мы не поворачиваем на случайный угол, а вертикальные отрезки просто игнорируем. Не понимаю, где это может не работать. Гарантируется же, что точка запроса не может лежать на отрезке.

В итоге у нас WA4, но я думаю, не по этой причине.

→ Ответить

9 лет назад, # ^ |

Мне кажется, что в этом очень легко ошибиться. Очень сложно подобрать правильный порядок, в котором надо разбирать события на одной вертикальной прямой. Когда мы с Лёшей обсуждали, как это делать, на каждый вариант порядка получалось найти контртест. Вот парочка подставных случаев, можешь попробовать на них потестить.

Картинка: http://i.imgur.com/8qFG0YS.png

→ Ответить

9 лет назад, # ^ |

Спасибо. На глаз всё должно работать, но надо запустить решение, вдруг оно глупее меня окажется.

→ Ответить

Edvard

9 лет назад, # ^ |

Мы сдали все тоже самое, но без выкидывания мостов и поворота на рандомный угол. Получилось все в целых числах, вертикальные отрезки просто игнорим. Кода было до фига.

→ Ответить

riadwaw

9 лет назад, # ^ |

Иногда, когда ты проходишь по такому отрезку, ты выходишь из многоугольника, иногда нет.

Зависит в одну до сторону соседние отрезки.

→ Ответить

qwerty787788

9 лет назад, # ^ |

+16

Как обычно :)

Вначале выделим все многоугольники (т. е. для каждого многоугольника найдем его обход, например, против часовой стрелки). Теперь для каждого ребра мы знаем в какую сторону оно направлено или что оно направлено в две стороны и его можно не учитывать.

Сделаем сканлайн и в декартовом дереве будем хранить ребра. При этом, если ребро идет слева направо с коэффициентом +1, а если справа налево, то -1. Чтобы определить, находится ли точка хотя бы в одном многоугольнике, спустимся по дереву и найдем префикс сумму. Если она отлична от нуля, то значит точка лежит внутри многоугольника.

Еще в самом начале можно все повернуть на случайный угол, чтобы не думать о крайних случаях.

→ Ответить

Kaban-5

9 лет назад, # |

Как решать C?

→ Ответить

qwerty787788

9 лет назад, # ^ |

+16

Отсортируем q запросов по длине кратчайшего пути (измеренного в количестве ребер). Легко доказать, что для некоторого префикса запросов в этом порядке мы будем доставлять еду по кратчайшему маршруту, а для остальных по пути, который направлен для всех в одну и ту же сторону. Переберем в какую именно сторону будет доставляться еда для суффикса.

Необходимо определить, для каких именно префиксов можно доставлять еду по кратчайшему пути. Существует две причины из-за которых префикс может считаться невалидным:

Существует два запроса, для которых мы хотим доставить еду по кратчайшему пути, эти два пути пересекаются и направлены в разные стороны.
Существует запрос, для которого мы хотим доставить еду по кратчайшему пути, а также существует запрос из суффикса, эти два пути пересекаются и направлены в разные стороны.

Чтобы найти противоречие первого типа, будем идти по порядку запросов и в каком-нибудь дереве отрезков проставлять +1/-1 (в зависимости от направления) пока не получится так, что в какую-то клетку (которая соответствует некоторому ребру) захотим поставить два разных числа.

Чтобы найти противоречие второго типа для каждого запроса, направленного в "неправильную сторону", найдем максимальный запрос, который с ним противоречит. Для этого заведем дерево отрезков на максимум, и будем идти по запросам с конца и каждый раз заполнять еще не заполненные клетки id-шником текущего запроса.

Потом для каждого валидного префикса посчитаем его стоимость и обновим ответ.

→ Ответить

9 лет назад, # ^ |

← Rev. 2 →

Это решение, наверное, не самое простое, но кода довольно мало:

Есть два варианта: 1) либо всё ориентируем по циклу в одну из двух сторон. 2) есть вершина, из которой оба ребра выходят.

Первый вариант понятно как считать, давайте научимся считать второй. Для каждого задания у нас есть два способа выполнить его — в одну сторону по циклу, и в другую. Если мы зафиксировали "особую" вершину, из которой оба ребра выходят, то для всех заданий, кроме тех, у кого конец особый, мы однозначно знаем, как их нужно выполнять. А их тех, у кого конец "особый", ясно, что какой-то префикс в отсортированном порядке идёт налево, а остальные направо (так как эта вершина "особая", то в неё не входит ни одного задания).

Давайте теперь передвигать "особую" вершину по циклу, и поддерживать, как мы выполняем каждое задание. При обработке очередной "особой" вершины в начале все задания из неё идут направо, и мы их по одному перекидываем налево в отсортированном порядке.

Всего будет O(N) перекидываний, так что нужно лишь иметь структуру, которая умеет говорить, есть ли при заданном способе выполнения заданий противоречие. Например, подойдёт дерево интервалов, которое для каждого отрезка помнит "есть ли там рёбра налево" (ну точнее чтобы поддерживать "есть ли", видимо нужно помнить сколько), "есть ли там рёбра направо", "есть ли там противоречия".

→ Ответить

9 лет назад, # |

Подскажите как решать B быстрее чем за N^2logN без большого количества кода? Ели запихали сжатые координаты + map + lower bound, была идея со списками за N^2, но там пришлось бы писать много кода. Желательно с ссылками на реализацию. Спасибо.

→ Ответить

9 лет назад, # ^ |

Списками. Без шаблона кода строк сто, но он размашистый и очень простой.

→ Ответить

9 лет назад, # ^ |

Классная идея хранить все итераторы, чтобы удалять за констатну и не использовать двухсвязные не STL списки.

→ Ответить

9 лет назад, # ^ |

Вот моё решение со списками — немного копипасты, но в целом простое: http://pastebin.com/idsQa8WZ

→ Ответить

9 лет назад, # ^ |

Спасибо, симпатичных двухсвязный список.

→ Ответить

ivan.popelyshev

9 лет назад, # ^ |

Для каждой вершины хранить соседние на 4 стороны (сортировка за N log N). Для каждой начальной точки копируем всю структуру, чтобы можно было удалять вершины когда мы прошли по ним. В итоге N*N

→ Ответить

9 лет назад, # ^ |

Заходит без проблем за N^2 log N, с пересчетом структуры для каждой начальной точки.

→ Ответить

9 лет назад, # ^ |

Забавно, что такая задача встречалась на CF больше четырёх лет назад в ограничениях 5000, и народ тогда тоже пытался пихать $\text{[math]}$ , но не преуспел в этом.

→ Ответить

9 лет назад, # ^ |

Ага, я тоже вспомнил и именно поэтому побоялся лишний логарифм писать.

→ Ответить

permin

9 лет назад, # ^ |

Как и 4 года назад мне потребовалось некоторое время, чтобы заметить, что поля 5000 × 5000 не бывает :)

→ Ответить

Edvard

9 лет назад, # ^ |

у нас было решение с DSU, которое хранило следующую не удаленную из текущей вершины.

→ Ответить

TigranHakobyan

9 лет назад, # |

Как решать F ?

→ Ответить

9 лет назад, # ^ |

Динамика.

Сначала для каждой вершины посчитаем лучшую дорогу от нее для выступления, т.е. с максимальным v/d(т.е. максимальный результат за секунду), пусть это будет массив best_road[i]

После этого напишем динамику dp[time][v] — максимальный результат, который можно достичь за time секунд от начала на v вершине.

Основа динамики dp[0][1] = 1, для каждого ребра(x,y) переходы dp[i+d][y] = max(dp[i+d][y],dp[i][x] + v), dp[i+d][x] = max(dp[i+d][x],dp[i][y] + v)

Ответом будет максимум dp[time][v]*2 + (P-time*2)*best_road[v] по time = 0..P/2, v = 1..n

→ Ответить

NVAL

9 лет назад, # ^ |

+17

Можно проще:

посчитаем динамику dp[v][time]: для каждой вершины v наилучший результат, что мы закончим в этой вершине во время time. Переходы по ребрам в соседние вершины и в саму себя во время time+1 по наиболее выгодному ребру выходящему из этой вершины

→ Ответить

riadwaw

9 лет назад, # ^ |

переходы по time+1 можно по всем ребрам сделать — на сложность не влияет.

→ Ответить

9 лет назад, # ^ |

Есть только одна вершина, в которой мы будем стоять на месте, переберем ее, когда мы знаем где стоим с эффективностью v/d, мы можем найти путь по ребрам Исходная цена-V/d, чтобы этот путь был мнимален по такой цене. При этом идти только по ребрам с положительной ценой(иначе будет находить пути с большим временем, но положительной эффективностью), получаетс N *N^2.

→ Ответить

9 лет назад, # |

← Rev. 3 →

+14

Кто знает почему в дорешивании на opencup.ru нет задач C,E,I? На yandex есть все задачи, но когда пытаешься отправить решение, выходит Your solution was not submited.

UPD Все в yandexе можно отправлять.

→ Ответить

nfssdq

9 лет назад, # |

Can anybody share their solution of D, I and J?

→ Ответить