| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Suppose we have n set of numbers . we want to choose a number from each set that they were distinct . how we can do it efficiently ?
A -> 1 <= n <= 20 , 1 <= |s| <= 100 , 1 <= numbers <= 10^9
B -> 1 <= n <= 10^5 , 1 <= |s| <= 10^5 , 1 <= numbers <= 10^9
C -> In General ?
thanks in advance.
Auto comment: topic has been updated by Frez (previous revision, new revision, compare).
Denote the n sets as (Ai)i = 1..n, then let
. Now consider a bipartite graph with a vertex for each set on the left side, a vertex on the right set for each element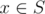 
, and an edge from the vertex representing set Ai to the vertex representing the element x if and only if 
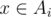. Clearly any maximum bipartite matching induces a selection of elements from the sets such that each element is distinct (prove this yourself).
In other words, the problem can certainly be solve in polynomial time. However, the complexity isn't great. The number of vertices is n + |S| (recall that S is the set of distinct elements), and the number of edges is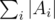
. Hopcroft-Karp gives an 
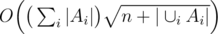algorithm. (Note: using a appropriate datastructures (maps etc) this reduction takes 
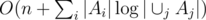time, it is important that the complexity of the new problem supersedes the complexity of the reduction).
However, the reduction works the other way around. Given a bipartite graph, denote the left side as V1 and the right side as V2. For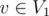
, let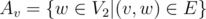 
. If we can select a distinct element from each set, this clearly induces a complete bipartite matching. Note that this reduction takes O(V1 + V2 + E) time, less than the best known bound on bipartite matching.
In other words, this problem is equivalent to deciding whether a bipartite graph has a maximal matching.
EDIT: Hopcroft-Karp is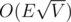
, not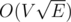 
.
THANKS:) really awesome! This was hard for me to understand but I got it finally.
related problem is here. I hope I can solve it now :D
That problem is a bit different from the one you mentioned above (or maybe I misinterpreted it). But you can also solve it using bipartite matching.
I just tried the problem and (as expected) it worked. Of course I would recommend first trying it yourself, but if you can't figure it out, here is my solution. All relevant code is in the main (the rest is just generic max flow code), I added some comments to make everything clear.