Блог пользователя thebruisedsoul

How to handle large number of queries related to finding LCM of all numbers in the range [L,R]??
Автор thebruisedsoul, история, 9 лет назад, По-английски

I am trying to solve this problem, which provides an array of N integers , and requires to compute for M number of queries LCM of all the elements of the array in the range of indices [L,R] . As the answer can be very large print it modulo 10^9+7. 1<=M<=100000 1<=L<=R<=N. Please help to solve this problem.

  • Проголосовать: нравится
  • -11
  • Проголосовать: не нравится

»
9 лет назад, # |
  Проголосовать: нравится -8 Проголосовать: не нравится

Please provide a link to the problem.

→ Ответить
»
9 лет назад, # |
  Проголосовать: нравится +5 Проголосовать: не нравится

I have not found any information about the start and the end of the contest this problem is from on Hackerrank. It seems I need to sign up to see this, such a strange behaviour of the system. So I can't be sure the contest has ended, though I have some thoughts about the problem.

→ Ответить
  • »
    »
    9 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится

    The contest has ended. For your convenience let me paste the problem statement here .

    Problem Statement

    vedaytas likes challenging professors at his school and this time he has challenged his mathematics professor. The professor was teaching a boring bookish method of calculating least common multiple of N integers.While he was mid-way explaining the procedure,vedaytas stood up and interrupted him and said that he had better way of performing the job.The aged professor felt offended at being interrupted in the middle and poses vedaytas a challenge that given list of N numbers,if he could answer his M queries correctly then he will be awarded with Ex-grade otherwise will be given a F-grade.Your job is very simple.Help vedaytas get an Ex-grade as for him now it is a matter of pride.

    Query Format:

    For each query vedaytas is given two numbers l and r (1-based indexing) and he needs to answer the lcm of the numbers at positions l,l+1,l+2,...,r

    Input Format

    First line contains T the number of test cases

    For each test case we have the following information:

    First line contains N the number of numbers in the list

    Next line contains N space separated integers

    Next line contains M the number of queries

    Next M lines we have two space separated integers l and r

    1<=T<=10

    1<=N<=100000

    1<=Number in the list<=10^9

    1<=M<=100000

    1<=L<=R<=N

    NOTE : It is assured that the total number of queries in a test file doesnot exceed 10^5

    → Ответить
    • »
      »
      »
      9 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      I think this can help. For every prime, you need to maintain it's maximal power in the current segment. The overall number of prime divisors of all numbers in the input is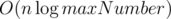 . Futhermore, each number contains at most 9 different prime divisors. Using this, you can obtain some kind of solution in 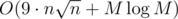time.

      → Ответить
      • »
        »
        »
        »
        9 лет назад, # ^ |
          Проголосовать: нравится +3 Проголосовать: не нравится

        I have solution in O(N * factorization(Amax) + MlogN).

        → Ответить
      • »
        »
        »
        »
        9 лет назад, # ^ |
        ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

        It's easier if you see lcm as product/gcd. Modulo being prime,you can use fermat's theorem ((x/y)%MODULO = ((x%MODULO)*((y^(MODULO-2))%MODULO))%MODULO But it seems that gcd modulo is not a good choice.

        Another solution is using Mo's algorithm with complexity O(M*sqrt(n)*log*9).Log is for keeping the max value at every prime factor.

        → Ответить
        • »
          »
          »
          »
          »
          9 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится

          Your claim is true only for two numbers. For example, 6, 10, 15: their lcm is 30, but product/gcd is 900. Anyway, interested in faster solution.

          → Ответить
          • »
            »
            »
            »
            »
            »
            9 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится

            My solution was based on rmq table,partitioning [l,r] in max log lcms and then doing lcm on them(two by two),but this doesn't work when things are made MODULO.

            → Ответить
      • »
        »
        »
        »
        9 лет назад, # ^ |
          Проголосовать: нравится +8 Проголосовать: не нравится

        How will you compute the prime factorization of the numbers?

        → Ответить
»
9 лет назад, # |
  Проголосовать: нравится -18 Проголосовать: не нравится

Segment Tree

→ Ответить
»
9 лет назад, # |
← Rev. 3   Проголосовать: нравится -24 Проголосовать: не нравится

Not sure if this will be helpful.

Edit: I was completely incorrect. Sorry about misleading you!

→ Ответить
»
9 лет назад, # |
  Проголосовать: нравится -14 Проголосовать: не нравится

This is probably the problem he is trying to solve: https://www.codechef.com/OCT15/problems/LOTERY

Check his submissions: https://www.codechef.com/users/thebruisedsoul

→ Ответить
»
9 лет назад, # |
  Проголосовать: нравится -14 Проголосовать: не нравится

I got that problem accepted with just a regular LCM Segment tree.

→ Ответить
»
9 лет назад, # |
← Rev. 2   Проголосовать: нравится -14 Проголосовать: не нравится

can some one explain why this code dont work? thanks

const i64 MOD = 1e9+7;

int st[maxn*4], tmp[maxn];

int n, q, T;

int nextPow2( int x){
    int p = 1;
    while( p < x )p<<= 1;
    return p;
}

int inv(int a, i64 e){
    i64 ret = 1ll;
    i64 p = a;
    while( e ){
	if( e&1 ){
	    ret = (ret*p)%MOD;
	}
	p = (p*p)%MOD;
	e >>= 1;
    }
    return (int)(ret % MOD);
}

int main(){
    //clock_t c = clock();
    for( io>>T; T; --T){
	io>>n;
	int p = nextPow2(n);
	fill( st+p, st+(p<<1), 0);

	for( int i = 0; i < n; ++i)
	   io>>st[p+i]; 
	for( int i = p-1; i > 0; --i){
	    int l = i<<1;
	    int r = l+1;
	    int gc = inv(__gcd(st[l], st[r]),MOD-2ll);
	    st[i] = (int)((((1ll*st[l]*gc)%MOD)*st[r])%MOD);
	}
	int vl, vr;
	for( io>>q; q; --q){
	    int l, r;io>>l>>r;
	    if( l > r)swap(l,r);
	    l += p-1;
	    r += p-1;
	    vl = st[l];
	    vr = st[r];
	    l >>= 1;
	    r >>= 1;
	    while( r != l){
		{
		    int gc = inv(__gcd(vl, st[(l<<1)+1]),MOD-2ll);
		    vl = (int)((((1ll*st[(l<<1)+1]*gc)%MOD)*vl)%MOD);
		}
		{
		    int gc = inv(__gcd(vr, st[(r<<1)]),MOD-2ll);
		    vr = (int)((((1ll*st[(r<<1)]*gc)%MOD)*vr)%MOD);
		}
		r >>= 1;
		l >>= 1;
	    } 
	    io<<(int)(((1ll*vl*inv(__gcd(vl,vr), MOD-2ll)%MOD)*vr)%MOD)<<endl;
	}
    }
	    
          
    return 0;
}
→ Ответить
»
5 лет назад, # |
← Rev. 2   Проголосовать: нравится +10 Проголосовать: не нравится

I have a question. How can we deal with the problem of calculating $$$LCM(l, l + 1, ..., r)$$$ % $$$(1e9 + 7)$$$ with $$$r - l + 1 <= 1e6$$$ and $$$l, r <= 1e14$$$ (1 query only) ?

Thanks for reading <3 <3.

→ Ответить
  • »
    »
    5 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится +6 Проголосовать: не нравится

    Put numbers $$$l$$$ through $$$r$$$ in an array and divide them by all the prime numbers up to $$$r - l + 1$$$, such that the remaining numbers would have only bigger prime factors (think of a fast way to do that, shouldn't be too hard). Take the product of the remaining numbers and multiply with the maximal exponent that you found for all the small primes. The idea is that if a prime factor bigger than $$$r - l + 1$$$ exists in the whole array, then it exists only once, so taking product of the remaining numbers is the same as taking product of the maximal exponents.

    → Ответить