Задачу подготовил adedalic.
В этой задаче сначала нужно было выкинуть все нули на префиксе и суффиксе строки, после чего ответ был равен количеству единиц плюс количество нулей с двух сторон от которых стоят единицы. Асимптотическая сложность решения: O(n).
Задачу подготовил Oleg_Smirnov.
Назовем путь i-м (0 ≤ i ≤ n - 1), если мы, выходя из дома, сначала i раз идем налево, потом переходим проспект и снова n - 1 - i раз идем налево. Введем обозначение di — время, которое нам придется ждать на светофорах на i-м пути. Если рассмотреть путь из магазина домой с конца, то получится пути из дома в магазиг, поэтому искомый путь есть два разных пути из дома в магазин. Значит ответом на задачу является сумма наименьшего и второго по величине значения di. Значение di легко пересчитывается из значения di - 1, таким образом все di можно посчитать за один проход.
Асимптотическая сложность решения: O(n).
Задачу подготовил Neon.
Заведем очередь в которой, будут находится дети. На каждой итерации решения пройдем по всем детям, если есть ребенок с отрицательной решимостью удалим его из очереди, а из решимостей детей с большими номерами вычтем di. Если все дети в очереди имеют решимость не меньше нуля, возьмем первого ребенка из очереди, а от решимостей остальных вычтем арифметическую прогрессию, как это описывается в условии.
Асимптотическая сложность решения: O(n2).
Задачу подготовил IlyaLos.
В задаче требовалось просто промоделировать игру. Это можно сделать с помощью обхода в глубину, ширину или динамического программирования. Состоянием является пара чисел x, y — позиция Филиппа в туннеле, а значением 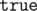 или
или 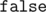 в зависимости от того, можем ли мы попасть из стартовой позиции в x, y. Положения поездов в каждый момент времени определяются однозначно.
в зависимости от того, можем ли мы попасть из стартовой позиции в x, y. Положения поездов в каждый момент времени определяются однозначно.
Асимптотическая сложность решения: O(n).
585C - Alice, Bob, Oranges and Apples
Задачу подготовил Edvard.
Поймем для начала, что означает процесс описанный в условии. Если нарисовать дерево переходов по буквам 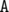 и
и  , то получится дерево Штерна-Броко. Пусть апельсины это значения знаменателя дроби, а яблоки — числителя. На каждом шагу у нас есть две дроби (изначально
, то получится дерево Штерна-Броко. Пусть апельсины это значения знаменателя дроби, а яблоки — числителя. На каждом шагу у нас есть две дроби (изначально 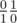 ) и мы заменяем либо первую дробь на их медианту, либо вторую. Таким образом, первая дробь есть первый предок влево от медианты, а вторая — первый предок вправо. Таким образом, искомый процесс это просто процесс поиска дроби в дереве Штерна-Броко, который завершается тем, что текущая медианта совпадает с дробью, которую мы ищем (момент окончания игры, описанный в условии). Значит, числа x, y заданные в условии это просто дробь, которую мы ищем. Отсюда следует, что ответа не существует, если x не взаимнопросто с y (поскольку таким дробей нет в дереве Штерна-Броко). Пусть теперь мы хотим найти дробь в дереве. Понятно, что если x > y, то мы сначала перейдем в правую ветку. Более того мы можем считать, что теперь ищем дробь
) и мы заменяем либо первую дробь на их медианту, либо вторую. Таким образом, первая дробь есть первый предок влево от медианты, а вторая — первый предок вправо. Таким образом, искомый процесс это просто процесс поиска дроби в дереве Штерна-Броко, который завершается тем, что текущая медианта совпадает с дробью, которую мы ищем (момент окончания игры, описанный в условии). Значит, числа x, y заданные в условии это просто дробь, которую мы ищем. Отсюда следует, что ответа не существует, если x не взаимнопросто с y (поскольку таким дробей нет в дереве Штерна-Броко). Пусть теперь мы хотим найти дробь в дереве. Понятно, что если x > y, то мы сначала перейдем в правую ветку. Более того мы можем считать, что теперь ищем дробь 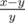 и никуда не спускались. Если же x < y, то нам нужно спуситься в левую ветку и можно считать, что мы ищем дробь
и никуда не спускались. Если же x < y, то нам нужно спуситься в левую ветку и можно считать, что мы ищем дробь 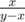 и пока никуда не спускались. Эти рассуждения легко формализовать, чтобы получить строгое доказательство. Таким образом, решение задачи сводится к выполнению алгоритма Евклида для пары чисел x, y. Как известно время работы алгоритма Евклида O(logn) (дольше всего алгоритм Евклида работает на двух последовательных числах Фибоначчи), значит длина ответа тоже растет как логарифм.
и пока никуда не спускались. Эти рассуждения легко формализовать, чтобы получить строгое доказательство. Таким образом, решение задачи сводится к выполнению алгоритма Евклида для пары чисел x, y. Как известно время работы алгоритма Евклида O(logn) (дольше всего алгоритм Евклида работает на двух последовательных числах Фибоначчи), значит длина ответа тоже растет как логарифм.
Асимптотическая сложность решения: O(logn).
Задачу подготовил danilka.pro.
Для решения этой задачи воспользуемся приемом 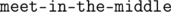 . А именно переберем для первых
. А именно переберем для первых 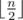 (первая половина) заданий с какими спутницами главный герой будет путешествовать. Пусть при этом симпатия первой спутницы оказалась равна a, второй — b, а третьей c. Пусть существует способ выбрать спутниц для последующих
(первая половина) заданий с какими спутницами главный герой будет путешествовать. Пусть при этом симпатия первой спутницы оказалась равна a, второй — b, а третьей c. Пусть существует способ выбрать спутниц для последующих 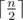 (вторая половина) заданий так и пусть симпатии при этом будут равны a', b', c'. Тогда, чтобы по всем заданиям суммы симпатий были одинаковы необходимо и достаточно, чтобы a - b = b' - a' и b - c = c' - b'. Теперь для решения задачи достаточно перебрать первую половину и сохранить в некоторой структуре данных тройки чисел a - b, b - c, a (третье число нужно для максимизации ответа в случае равенства). Далее нужно перебрать вторую половину и найти в структуре данных значения b' - a', c' - b', m, где m — максимальное третье значение которое есть в структуре данных. В качестве структуры данных можно использовать map < pair < int, int > , int > в языке C++, первые два числа это значение a - b, b - c, а третье — максимальное a соответствующее первым двум. Также можно все тройки сложить в один большой массив, отсортировать его и бинарным поиском находить необходимые значения.
(вторая половина) заданий так и пусть симпатии при этом будут равны a', b', c'. Тогда, чтобы по всем заданиям суммы симпатий были одинаковы необходимо и достаточно, чтобы a - b = b' - a' и b - c = c' - b'. Теперь для решения задачи достаточно перебрать первую половину и сохранить в некоторой структуре данных тройки чисел a - b, b - c, a (третье число нужно для максимизации ответа в случае равенства). Далее нужно перебрать вторую половину и найти в структуре данных значения b' - a', c' - b', m, где m — максимальное третье значение которое есть в структуре данных. В качестве структуры данных можно использовать map < pair < int, int > , int > в языке C++, первые два числа это значение a - b, b - c, а третье — максимальное a соответствующее первым двум. Также можно все тройки сложить в один большой массив, отсортировать его и бинарным поиском находить необходимые значения.
Асимптотическая сложность решения: 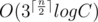 , где logC — константа, появляющаяся вместе со структурой данных.
, где logC — константа, появляющаяся вместе со структурой данных.
585E - Present for Vitalik the Philatelist
Задачу подготовил gridnevvvit.
Пусть мы хотим посчитать количество подмножеств с НОД равным 1 — число A. Посчитаем это количество с помощью формулы включений-исключений: сначала скажем, что все подмножества нам подходят. Таких подмножеств 2n. Теперь вычтем подмножества с НОД кратным 2. Количество таких множеств 2cnt2 - 1, где cnti — количество чисел, делящихся на i. Далее вычитаем 2cnt3 - 1. Подмножества с НОД кратным 4 мы учли вместе с двойкой. Далее вычитаем 2cnt5 - 1. Теперь заметим, что подмножества с НОД кратным 6 мы вычли уже дважды: сначала с двойкой, затем с тройкой, поэтому давайте прибавим количество таких подмножеств 2cnt6 - 1. Продолжая этот процесс получаем, что для числа d, к ответу нужно прибавить величину μ(d)(2cntd - 1), где μ(d) равно 0, если d делится на полный квадрат, 1, если количество простых в факторизации d четно и - 1 в противном случае. Значит числа, делящиеся на полный квадрат мы можем не суммировать, поскольку они входят с коэффициентом 0. Для подсчета значений cnti достаточно факторизовать все числа и для каждого за 2k перебрать делитель, со значением μ(d) ≠ 0. Теперь легко понять, что количество подмножеств с НОД большим 1 равно B = 2n - A. Теперь для решения задачи давайте переберем марку, которую купит Виталик ai. Пересчитаем число B так, как если бы числа ai не было в множестве. Для этого нужно просто вычесть те слагаемые на которые повлияло число ai. Это можно сделать за 2k, где k — количество простых в факторизации числа ai (снова нужно перебрать делители ai со значением μ(d) ≠ 0). Теперь поймем какие подмножества дадут НОД равный 1 вместе с выбранной маркой. Понятно это те подмножества НОД которых больше 1, но при этом не делится ни на один делитель ai. Для этого снова воспользуемся формулой включений-исключений. Для каждого делителя d числа ai вычтем из B значение μ(d)(2cntd - 1). Таким образом, мы получим количество способов Bi выбрать подмножество c НОД большим 1, но при это взаимнопростым с ai. Ответом на задачу является сумма всех Bi. Наибольшее количество простых в факторизации числа не превосходящего 107 равно 8. Факторизацию чисел можно выполнить с помощью линейного алгоритма поиска минимального делителя чисел от 1 до n, либо с помощью решета Эратосфена за время O(nloglogn).
Асимптотическая сложность решения: O(C + n2K), где 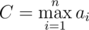 , а K — наибольшее количество простых в факторизации чисел ai.
, а K — наибольшее количество простых в факторизации чисел ai.
Задачу подготовил Edvard.
Расмотрим все подстроки строки s длины 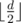 . Сложим все эти строки в бор, посчитаем суффиксные ссылки и построим автомат по цифрам. Это можно сделать за линейное время с помощью алгоритма Ахо-Корасик. Теперь для решения задачи посчитаем динамику zi, v, b1, b2, b в котором состояние описывается пятеркой чисел: i — количество цифр которые мы уже поставили в искомом числе, которое встречается
. Сложим все эти строки в бор, посчитаем суффиксные ссылки и построим автомат по цифрам. Это можно сделать за линейное время с помощью алгоритма Ахо-Корасик. Теперь для решения задачи посчитаем динамику zi, v, b1, b2, b в котором состояние описывается пятеркой чисел: i — количество цифр которые мы уже поставили в искомом числе, которое встречается 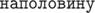 , v — в какой вершине бора мы находимся, b1 — равен ли префикс числа, которое мы набираем префиксу числа x, b2 — равен ли префикс числа, которое мы набираем префиксу числа y, b — находится ли некоторая подстрока длина
, v — в какой вершине бора мы находимся, b1 — равен ли префикс числа, которое мы набираем префиксу числа x, b2 — равен ли префикс числа, которое мы набираем префиксу числа y, b — находится ли некоторая подстрока длина 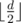 на уже набранном префиксе в боре (значения b1, b2, b — равны либо 0, либо 1). Значением динамики является количество способов набрать префикс с заданным набором свойств. Для того, чтобы сделать переход нужно перебрать цифру, проверить что мы не вышли за границы отрезка [x, y], перейти от вершины v к следующей вершине по автомату и заданной цифре. Ответом является сумма по всем v, b1, b2 zb, v, v1, v2, 1.
на уже набранном префиксе в боре (значения b1, b2, b — равны либо 0, либо 1). Значением динамики является количество способов набрать префикс с заданным набором свойств. Для того, чтобы сделать переход нужно перебрать цифру, проверить что мы не вышли за границы отрезка [x, y], перейти от вершины v к следующей вершине по автомату и заданной цифре. Ответом является сумма по всем v, b1, b2 zb, v, v1, v2, 1.
Асимптотическая сложность решения: O(nd2).











Все читают теги!
Чтобы увидеть, что там неправильный номер раунда?
Вы действительно считаете, что div. 1 F подходит по сложности на роль самой сложной задачи в div. 1 раунде из шести задач?
На самом деле задача F предполагалась по сложности равной задаче E.
Тогда почему E стоит 2250, а F — 3000 ?)
А что, вы её сдали на 10 минуте и она была слишком простой?
К сожалению, я слишком поздно её прочёл ^^"
Можно сказать, что я придумал её на 10 минуте после прочтения, потому что динамика совершенно классическая.
> div. 1 A
> Превышено ограничение времени на тесте 32
>.>
how can i get its english translation?
English translation will be ready soon.
Why is this 13576829 submission fails? I use 64-bit type here, so no overflow should occur. But is does...
13580842 AC
Oh, thank you! But... What is going on?! You've changed only the sizes of arrays, but they were large enough in both submissions.
Actually, the problem with your code was that you used scanf("%d") to read 64-bit integers, while the correct would be scanf("%I64d"). See 13584480 versus 13584478.
I can't say exactly why changing the array size from 4 × 103 to 5 × 103 made your solution pass, though. Maybe it just caused the array to be allocated in a place that was filled with zeros.
Your explanation is right, I found I used
%dto readlong long, but still got AC 13584293 ,seems interesting. Also 13584688 got WA32. I think it is because I defined the three arrays as global variables.Мне кажется, что в задаче уровня 2250-div1 не надо расписывать, что такое формула включений-исключений и функция Мёбиуса, достаточно дать ссылку. А то суть решения теряется за этими подробностями.
Мне кажется автору задачи виднее, что писать в разборе.
Ну и что, по-вашему, участники не могут сказать, что им не понравилось в разборе? Разбор для участников, между прочим. Конечно, я не вправе требовать что-то изменить в разборе, но высказать свою точку зрения все могут.
Ну-ну, грубить-то зачем.
Я и не грубил, а высказал своё мнение) тем более, что лично знаю сколько сил было потрачено авторами контеста в том числе на разбор. Ни в коем случае не хотел никому нагрубить и тем более обидеть.
"лично знаю сколько сил было потрачено на разбор"
Те, кто не лично, тоже знают. И что с того? Думаю, на подготовку задачи B вы тоже потратили много сил и времени. Тем не менее, допустили ошибку. Будьте открыты к критике.
Мне кажется, что наличие разбора с деталями лучше, чем его отсутствие. К примеру эту задачу может захотеть дорешать человек, который не знаком с формулой включений-исключений и обращением Мебиуса. Для такого участника будет полезно наличие объяснения формулы на пальцах, потому как, просмотрев какую-нибудь лекцию в интернете, или, прочитав в книжке про обращение Мебиуса, он увидит сухую формулу с алгебраическим доказательством (или без доказательства вовсе) и это никак не отложится в голове. Те же участники, которые считают себя слишком крутыми, чтобы читать разбор с подробностями, могут либо не читать его вовсе, а придумать это самому (ведь если он действительно крутой это несложная задача), либо просто проглядеть разбор, на наличие подсказок к решению. Например, когда я решаю/дорешиваю сложную задачу, я сначала пытаюсь придумать ее самому, а если в течении долгого времени не получается придумать проглядываю разбор на наличие подсказок и сразу закрываю его (например здесь, увидев функцию μ(d) я бы сразу закрыл разбор и додумал детали самостоятельно).
Но ведь разбор как раз для тех участников, которые недостаточно круты, чтобы решить задачу самостоятельно. Например, конкретно в этой задаче я понял про формулу включения-исключения и понял, что нам требуется функция Мёбиуса, но не догадался, как найти все cnti.
Ничего личного, но Вам не кажется несколько высокомерным считать, что по этому никак не структурированному двадцатистрочному абзацу с массой пунктационных ошибок (которые тоже затрудняют понимание текста) будет более понятно, что такое формула включений-исключений и функция Мёбиуса, чем по той же википедии, где это довольно понятно описано?
Разбор задач предназначен для всех. Даже очень крутые кодеры могут завести себя в тупик.
Я прямо сейчас открыл википедию и посмотрел, что там написано про функию и обращение Мебиуса: сухие формулы из которых не понятно, как это можно применить для решения задачи. В Грэхеме точно так же приведено алгебраическое доказательство по которому совершенно не понятно как так получается, что мы от функции на кратных/делителях переходим к чистой функции. Кстати определяется там функция не так как в вики и на мой взгляд в Грэхеме определение лучше, а формула из вики выводится.
Я никогда не думал, что в нашей среде программистов олимпиадников критически важными являются такие вещи как пунктуация. Мне всегда казалось, что программистам, математикам интересны только идеи, методы, подходы. Для проверки орфографии и пунктуации есть MS Word и факультет филологии. А так получается как в универе: если ты даже принесешь доказательство гипотезы Римана с неправильным шрифтом тебе скажут, что ты тупой и работа твоя шлак, а вот чувак который скопировал чью-то работу и заполнил ее красивыми картинками с правильным шрифтом молодец, респект ему.
Но ведь у вас в разборе ничуть не больше написано.
Ну, не передёргивайте. Я ведь не о шрифтах говорю и о пунктуации только заодно упомянул. А то можно ещё по-немецки разбор написать. Все идеи, методы и подходы тоже будут изложены и достаточно мотивированные товарищи даже смогут это прочесть. Идеи, методы, подходы — это всё да, но понятность изложения в разборе очень важна. От этого напрямую зависит, насколько ваш разбор будет полезен сообществу.
Конечно, достаточно мотивированные товарищи смогут понять любой разбор, а те, кому лень, даже открывать не станут, как бы он не был хорош. Но не надо так делить на чёрное и белое. Между ними есть очень большая прослойка людей (опыт подсказывает мне, что таких подавляющее большинство, в каком-то смысле — вообще все), которые будут или не будут вникать в разбор в зависимости от его краткости и понятности.
Я написал, что нужно делать включения-исключения, почему 4ку не надо учитывать, почему 6ка с минусом. Эти рассуждения легко продолжить и вывести формулу самостоятельно.
На счёт утверждения, что для большей части аудитории важна краткость и понятность изложения я немного сомневаюсь: почти всегда кодеры олимпиадники понимают друг друга с полуслова и детали рассуждения опускаются.
И несмотря на все эти соображения, в задаче С дерево на Штерна-Броко дана ссылка, а в задаче F бор и алгоритм Ахо-Карасика просто упомянуты.
Спасибо за замечение уже поправил.
Не в этом дело. Непонятно, почему в этих задачах тоже не объясняются вкратце эти понятия.
Потому что тот кто знает эти алгоритмы поймет идею решения, в ином случае мне кажется, что очень сложно понять Ахо-Корасика из краткого описания
Опечатка: необходимо и достаточно, чтобы a - b = b' - a (Минус a')
Спасибо. Поправил.
"If x > y, we should firstly go in the right subtree. Moreover, we could then consider we are searching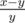 from the root. If x < y, we should go left and next consider
from the root. If x < y, we should go left and next consider 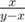 from the root."
from the root."
Could you explain the intuition behind this? I have a hard time seeing how this fits in the the Stern-Brocot tree.
Me too. I am still not able to figure out why it fits into Sterm-Brocot tree. It fits as the editorial says but I have no Idea what is the intuition behind it! Why should it fit into that form ? English translation is so poor that I have to guess meaning of every line :( Not a single line is English sentence !
I could figure it out partly as:
Let x/y be x number of apples drawn out, and y number of oranges drawn out from the bag. Now, say you have drawn out x/y and are at some branch of the tree, What happens when a card draws out? All the x/y get transferred to the other person. And some more apples and oranges are drawn out from the bag. How do we get this number?
It can be seen from the stern brocot tree that the new number is the median — (x+x1)/(y+y2) of it's parent, and the one in it's region.
I don't get the intuition either... but I will share what I managed to grasp until this point (although I can't fully say I understand everything I will mention in this post)
From what is said in the editorial, "If x > y, we should go to the right subtree," it seems that when the fraction x/y is greater then 1 then the answer always lies in the right subtree. Then, "Moreover, we could consider we are searching for (x-y)/y from the root" seems to suggest that we can now put ourselves at the new root without caring how we got here, and just search for (x-y)/y — which importantly (?) is exactly 1 less than x/y.
I will give an example of why this works, although I don't know exactly the reason behind it yet. Draw out the Stern-Brocot tree for about 5 levels including the root 1/1, and now let's look for fraction 7/4. 7 > 4, so we go to the right subtree and look for (7-4)/4 = 3/4. At this point, note that we came from the node 1/1 (looking for 7/4) and we are now on node 2/1 (looking for node 3/4). Now, note that 3/4 and 7/4 are in the same position relative to nodes 1/1 and 2/1, respectively...
Now let's look at the case where x < y. Let's look for 2/5. From node 1/1, we next go to node 1/2 and look for 2/(5-2) = 2/3. Similar to the case where x > y, 2/3 and 2/5 are in the same position relative to nodes 1/1 and 1/2, respectively!
The observation above indeed proves that the algorithm is correct, but I have yet to understand why it is works...
Hope someone can explain why it is works...
Do you know there is a book called 《Concrete Mathematics》 ? In this book, you can turn to page 121, and you will get what you want in details :)
"root" means root of the whole tree.
Possible I can answer this quistion
Let's make a 2*2 matrix
((a,a'),(b,b'))
a means the first person's apple
b mean's the first person's orange
Let's think about the operation B ((a,a'),(b,b')) * ((1,0),(1,1)) = ((a+a',a'),(b+b',b')) so we make B=((1,0),(1,1))
Let's think about the operation A ((a,a'),(b,b')) * ((1,1),(0,1)) = ((a,a+a'),(b,b+b'))
so we make A=((1,1),(0,1))
Let's define a function f:
f((a,b),(a',b'))=(b+b')/(a+a')
then we can find that:
if S is a statement ((a,a'),(b,b'))
then f(B*S)=(a+a' + b+b')/(a+a')=f(S)+1
so if f(B*s)=m/n f(s)=(m-n)/n if f(A*s)=m/n f(s)=m/(n-m)
so if (n>m) we can know the first step is A and then we need to find m/(n-m) if (m>n)we can know the first step is B and then we need to find (m-n)/m
i'm sorry for that i don't know how to write math formula in the codeforces... i'm sorry for my poor English..
Let A(x, y) = (x, y + x) and B(x, y) = (x + y, y). Note that A and B are linear transforms, meaning that A(a, b) + A(c, d) = A((a, b) + (c, d)) and likewise for B. Additionally, let (x, y)sum = x + y.
We are trying to find a function M (composition of As and Bs) such that M(1, 0)sum = x and M(0, 1)sum = y. Call (x, y) reachable if such a function M exists. Let x > y without loss of generality. We are trying to prove that (x, y) is reachable if and only if (x - y, y) is reachable. We will only prove the forward case here. The backwards case follows a similar argument.
Statement (forward case): If (x, y) is reachable, then (x - y, y) is reachable.
Proof: If (x, y) is reachable, then by definition there exists a function M such that M(1, 0)sum = x and M(0, 1)sum = y. Note that the since x > y, the inner-most function of M must be an A. There then exists an L such that M = L(A()). Note that L(0, 1)sum = L(A(0, 1))sum = M(0, 1)sum = y and L(1, 0)sum = L(A(1, 0) - (0, 1))sum = L(A(0, 1))sum - L(0, 1)sum = M(1, 0)sum - L(0, 1)sum = x - y. Hence, (x - y, y) is reachable through L.
Can anyone explain me how to solve Div2 Problem D in detail?
Suppose that trains are fixed and the person do moves as follows: 1. Move right 2. Move up or move down or don't move 3. Move right 4. Move right
Then, you can solve this problem with DP. You can see my code. http://codeforces.net/contest/586/submission/13563032
hi:) first ty for The contest,i got Wrong Answer in Problem C(Div 2),i really dont know why!:( can any one help me??:( ( my algorithm is O(n) ) http://codeforces.net/contest/586/submission/13590330
Consider this input:
Your answer is 1 2 4 and it should be 1 2. First kid scare off third one and there are two remaining, one goes in and scare the other. Your solution tries to compute everything in one go, but every time you need to compute decreasing scream first and then do the runnning. Hence O(n^2) complexity. Hope this helps.
Got it:) Thank you so much...
the time limit for Div.1 D seems a little strict. There are many accepted solutions with time >=1500ms , and many who failed because they exceed the TL by a small amount, even though they used the same algorithm as the editorial.
Yes, it is, I spent ~20 mins optimizing my solution ._.
If you use "map" twice, you will get TL. Just use it once, you can AC.
Hi, does anyone know if there is another solution for "585C — Alice, Bob, Oranges and Apples" (div1 C) ? Do I have a method to solve it if I don't know Stern-Brocot tree ? Thanks!
My teammate danilka.pro solved it without knowing about Stern-Brocot tree.
Slightly weak tests on div 1 D:
Some solutions that sort the resulting values will not find the maximum answer correctly, and some solutions using a map will overwrite previous values in a map keyed by pairs of differences. Most such solutions fail on this test:
where the only correct solution is to take all the 1's. For example this practice solution of mine which is clearly wrong due to this passes: 13576496. For an example contest submission that fails, see 13565708. (thus it's not a small bug specific to my implementation)
Also BTW my purpose in making these posts is to let others know their solution may not be correct. I'm not blaming anyone; I know this kind of thing inevitably happens. My goal in solving problems is not to get AC, but to have a correct solution, and I will try to fix any AC solution if it isn't completely right. I try to help others with similar goals.
Thank you for test-case. It was added to upsolving.
Wow, I didn't know you could do that. Thanks!
In problem Div2/D can any one explain why these are the possibles moves :
s R R R
or
s R U R R
or
s R D R R
( U=Up R=Right D=Down )
13563714
from the problem statement, the valid moves are R,RU,RD , then the trains will move two steps to the left, which is equal to the person moving two steps to the right, so RRR,RURR,RDRR
I got it thanks :)
For Div 1 E:
Should be μ(d)(2cntd - 1) instead.
Fixed thanks. Missed μ(d) when translating to English.
Does anybody solve 585A on Python? I guess it's impossible to pass test 32 using Python as programming language
Status > Verdict:Accepted + Language:Python2/3 > Nobody solved, but some solutions are with PyPy2/3. Python and other scripting languages are to slow for these constraints?
I have solved it simply resend my solution with pypy 2.5 instead of python 2
13652262 2015-10-15 22:52:35 shade33 C — Стоматолог Геннадий PyPy 2 Полное решение 296 мс 8200 КБ 13651833 2015-10-15 22:44:33 shade33 C — Стоматолог Геннадий Python 2 Превышено ограничение времени на тесте 32 1000 мс 900 КБ
How about now? Does anybody solve 585A on Python? I also think it is almost impossible.
I haved passed 72 tests. I don't know how to pass more.
Can you help me?
Solved Div1 F using Suffix Automaton. I think it's a nice problem for Suffix Automaton. This process don't need any pre-processing of d/2 length substrings. Nice problem in deed :)
The memory limits for div1 E are strict for solution given in editorial. How do you keep 8 factors of 107 numbers, that will be 8 * 107 which is around 320MB and can't be kept in 256MB limit. I could not use vectors as well. Can you provide code?
We can also view problem C Div 1 geometrically like this:
First, we have two vectors A(1, 0) and B(0, 1) and our target is vector C(x, y)
To reach target C, we can do two operations, either transform A = A + B, or B = A + B. We are done when A + B = C
if x == y, we cannot have a solution.
if x != y, we notice that, the angle (A, C) and (B,C) are always in opposite directions. Which means, in clockwise order, we have vector A -> C -> B. So, our task becoming, transform vector A into A + max*B with max is the maximum number that maintain order A -> C -> B, max can easily be found using binary search.
My submission
Thanks buddy.! This one was the best solution and was quite logical. I couldn't have solved this one if you didn't comment this. Solution
Problem Gennady the Dentist was good experience for me to think about O(n) idea.
In Div2D testcase 6, there is a train of length 1.
585A . Gennady the Dentist ... Of course there are much faster solutions not required in our case.
How we can do better ? It seems we have to simulate every thing and I can't find any solution! Am I wrong ?