Блог пользователя xeronix

Area of union of circles
Автор xeronix, 13 лет назад, По-английски

Can anyone explain the algorithm to solve area of union of circles problem( given n circles + centre and radius of each)

Thankyou

  • Проголосовать: нравится
  • +16
  • Проголосовать: не нравится

13 лет назад, # |
← Rev. 4   Проголосовать: нравится +6 Проголосовать: не нравится

I don't understand how it can be in logarithmic time complexity, because it must be at least O(n).

The main idea of counting the area of union of some figures is that we draw vertical lines throug the "interesting" points ans solve the problem in each of the stripes between two adjacent lines.
The interesting points here will be the most left and right points on each circle and all the intersection points. There will be O(n2) interesting points.
Inside each stripe there will be some disjoint arcs, so we can sort all the arcs by their y-coordinates and count the area of union in O(n) complexity using, may be, stack (that arcs will form correct parthenesis sequence) and some integrals.
So we have the O(n3 log n) algorithm. It can be reduced to O(n2 log n) by looking on the coefficients in the integral and understanding how they change from strip to strip, so we can use some data structure to update them fast.
→ Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    Can you please elaborate the steps after sorting of arcs.
    → Ответить
    • 13 лет назад, # ^ |
      ← Rev. 3   Проголосовать: нравится +5 Проголосовать: не нравится

      You have a sequence of disjoint arcs, right? They organize pairs - arcs are in pair if they are from common circle. Let the top of them be opening arc and the bottom is closing. That pairs organize "segments" of area, union of which we should count.

      Do you know how to find the length of the union of the segments on the line in O(nlogn)? Here is the same: when we process opening arc and the balance is 0 we add area under this arc to the sum. When we process closing arc and balance becomes 0 (or, the same, balance is currentlty 1) we substract the area under this arc from sum.

      UPD: The balance is the difference between opening arcs and closing arcs. Oblivious that it is non-negative at all the time.
      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится
        Ok, now i got the approach. But finding area under an arc seems to be quiet complex( as i have never written any code dealing with integrals :) ).
        → Ответить
        • 13 лет назад, # ^ |
            Проголосовать: нравится +5 Проголосовать: не нравится
          This summer I've written it for the first time too in our Winter part of Summer Informatics School.

          That was brainsmashing. Hours of debugging...
          Advice: if you decide to write it, insert lots of asserts to check wheter variable under square root/arctan/denumerators of rationals are all correct. It will save your time.
          → Ответить
13 лет назад, # |
← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится

Мне интересна другая вариация задачи: "Любые две окружности могут иметь одну точку пересечения или одна окружность лежит внутри другой. Посчитать общую площадь занимаемую окружностями."
Может ли кто-нибудь подсказать решение за O(n log n)? Заранее спасибо
→ Ответить
  • 13 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится

    Нам нужно выкинуть те окружности, которые лежат внутри других, и просто просуммировать площадь остальных. 
    Отсортируем окружности по убыванию y+r (их верхней точки), а при равенстве - по убыванию радиуса. Понятно, что при таком порядке добавления внутренняя окружность будет добавлена всегда после своей внешней. Добавляем только внешние окружности (те, которые не лежат внутри кого-то) и храним их в сете отсортированными по x-координате центра (тут может быть баг и нужен изменяемый компаратор, но я не уверен). Разумеется, каждую окружность из сета надо своевременно удалять.
    Когда добавляем окружность, смотрим, на какое место в сете она должна встать. Если она не лежит внутри какой-то из соседних, то добавляем ее в сет и прибавляем к ответу площадь, иначе игнорируем.
    UPD. Возникли вопросы по поводу удаления окружностей из сета. Делаем это сканлайном. Для каждой окружности есть два события. Первое, с координатой y+r (верхняя точка окружности) - добавление. Как его делать, я описал выше. Второе, с координатой y-r (нижняя точка) - удаление. Если окружность, которой соответствует текущее событие удаления, была добавлена в сет ранее, удалим ее. Иначе снова проигнорируем.
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Никто не гарантирует тебе, что окружность может быть только внутри соседней. Если у тебя картинка вида

      ....OOO...
      ..._____..
      ../.....\.
      ..|....O|.
      ..|.....|.
      ..\_____/.


      и ты добавляешь нижнюю маленькую окружность, то соседними ей будут куча маленьких окружностей сверху, а не объемлющая её. Хотя, может я не очень понял, как ты будешь удалять (точнее, когда) окружности из сета.
      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится +5 Проголосовать: не нравится
        Куча маленьких сверху к тому времени уже будут удалены из сета. У нас сканлайн, в котором есть события добавления окружностей и иногда появляются события удаления.
        → Ответить
        • 13 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится
          Ты уточни, когда именно мы удаляем окружность.
          → Ответить
          • 13 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится
            Окружность удаляем, когда доходим до ее нижней точки (y-r). По-моему, это очевидно - именно в этот момент она перестает быть нужна. Сейчас внесу это в пост.
            → Ответить
13 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится
I am interested in another variation of this problem: "Any pair of circles can have one intersection point or one circle can be inside another. Calculate total area covered by circles. "

Can anyone help with O(n log n) solution? Thanks in advance.
→ Ответить
  • 6 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    This problem literally asks you to eliminate the circles that are inside some other circle and add up the areas of the dominating circles.

    You can check if a circle is inside another using sweepline.

    Main idea:

    Spoiler
    → Ответить
»
6 лет назад, # |
← Rev. 3   Проголосовать: нравится +20 Проголосовать: не нравится

This can be solved using Green's Theorem, with a complexity of n^2log(n). If you're not familiar with the Green's Theorem and want to know more, here is the video and notes from Khan Academy. But for the sake of our problem, I think my description will be enough. The general equation of Green's Theorem is

If I put L and M such that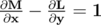

then the RHS is simply the area of the Region R and can be obtained by solving the closed integral or LHS and this is exactly what we're going to do.

All unions can be broken into such disjoint sets of circles which intersect

So Integrating along the path in the anticlockwise gives us the Area of the region and integrating along the clockwise gives us negative of the Area. So

AreaOfUnion = (Integration along red arcs in anticlockwise direction + Integration along blue arcs in clockwise direction)

But the cool trick is if for each circle if we integrate the arcs which are not inside any other circle we get our required area i.e. we get integration in an anticlockwise direction along all red arcs and integration along all blue arcs along the clockwise direction. JOB DONE!!!

Even the cases when a circle doesn't intersect with any other is taken care of.

Here is the GitHub link to my C++ Code

→ Ответить
  • »
    »
    6 лет назад, # ^ |
    ← Rev. 4   Проголосовать: нравится 0 Проголосовать: не нравится

    This code is not passing Area of Union of Circles on SphereOnlineJudge

    Problem Links:

    Any uncovered corner cases?

    → Ответить
    • »
      »
      »
      6 лет назад, # ^ |
      ← Rev. 3   Проголосовать: нравится +1 Проголосовать: не нравится

      I used the same approach and my solutions worked in both cases. There must some other problem in your code! Have you excluded the circles having the same center and radius? If some circles have the same centre and radius take only one of them.

      → Ответить
  • »
    »
    4 года назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    could you please explain how your code works?

    → Ответить