Codeforces Round #329 (Editorial)

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

593A - 2Char

Для каждой буквы будем поддерживать суммарную длину слов (cnt1_{c_i}), в которых встречается она одна, а для каждой пары букв будем поддерживать суммарную длину слов, в которых встречаются только они(cnt2_{c_i, c_j}).

Для каждой строки определим количество различных букв в ней. Если она одна, то добавим к этой букве длину этого слова. Если их две, то добавим к этой паре букв длину этого слова.

Переберем пару букв, которая будет ответом. Для пары букв c_i, c_j ответом будет cnt1_{c_i} + cnt1_{c_j} + cnt2_{c_i, c_j}. Среди всех таких пар найдем максимум и выведем его.

Решение за O(суммарная длина всех строк + 26 * 26)

593B - Антон и прямые

Заметим, что если i-я прямая пересекаются с j-й в данной полосе, а при x = x₁ i-я прямая находится выше, то при x = x₂ выше окажется j-я прямая.

То есть отсортируем прямые по координате y при x = x₁ + eps, и при x = x₂ - eps. Проверим, что порядок прямых в обоих случаях совпадает. Если существует такая прямая, что ее индекс в первом случае не совпадает со вторым, то выведем Yes. В другом случае выведем No.

Единственное, что может нам помешать это пересечение на границах, так как в таком случае порядок сортировки не определен. Тогда прибавим к нашей границе x₁ бесконечно малую величину eps, а от x₂ отнимем eps, и порядок сортировки будет задан однозначно.

Решение за O(nlogn)

593C - Красивая функция

Одним из ответов будет являться сумма таких выражений для каждой окружности по координате x и аналогично по координате y: 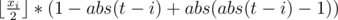$\text{[math]}$

Пусть a = 1, b = abs(t - i), тогда это можно записать как 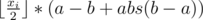$\text{[math]}$

Рассмотрим a - b + abs(a - b):

если a ≤ b, то a - b + abs(a - b) = 0,

если a > b, то a - b + abs(a - b) = 2a - 2b

теперь рассмотрим, что такое a > b:

1 > abs(t - i)

i > t - 1, и i < t + 1.

При целом i это возможно лишь в случае i = t.

То есть эта скобка не обнуляется лишь при i = t.

Рассмотрим 2a - 2b = 2 - 2 * abs(t - i) = 2. Тогда 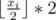$\text{[math]}$ отличается от нужной координаты не более чем на 1, но так как все радиусы не меньше 2, то эта точка принадлежит окружности.

Решение за O(n).

593D - Деревянный День Рождения

Рассмотрим задачу без запросов второго типа. Заметим, что в графе, где все числа на ребрах > 1 максимальное количество присвоений 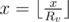$\text{[math]}$ до того, как x превратится в 0, не превышает 64. Действительно, если все R_v = 2, то количество операций можно оценить как log₂(x). Подвесим дерево за какую-нибудь вершину и назовем ее корнем.

Научимся решать задачу при условии, что для любого v R_v > 1 и нет запросов второго типа. Для каждой вершины кроме корня мы определили ее предка как соседа наиболее близкого к корню. Пусть у нас был запрос первого типа от вершины a до вершины b с иходным числом x. Разобьем путь на две вертикальные части, одна из которых приближается к корню, а другая отдаляется. Найдем все ребра на этом пути. Для этого посчитаем глубину каждой вершины как расстояние до корня. Теперь будем параллельно подниматься в дереве из обеих вершин, пока не встретимся в общей. Если в ходе такого подъема мы прошли более 64 ребер, то в ходе замен 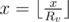$\text{[math]}$ мы получим x = 0 и мы можем на текущем шаге остановить алгоритм поиска. Таким образом, мы совершим не более O(log(x)) операций.

Перейдем к задаче, где R_v > 0. Заметим, что наше предыдущее решение в таком случае может работать за O(n). Так как при прохождении по ребру с R_v = 1 наше значение не меняется. Сведем эту задачу к выше рассмотренной. Сожмем граф, то есть уберем все единичные ребра. Для этого запустим dfs от корня и будем хранить самое глубокое ребро на пути от корня до вершины с R_v > 1.

Вспомним, что у нас были запросы уменьшения R_v. Будем поддерживать ближайшего предка P_v c R_{P_v} > 1. Воспользуемся идеей сжатия путей. При ответе на запрос первого типа будем пересчитывать P_v. Введем рекурсивную функцию F(v). Которая возвращает v, если R_v > 1, иначе выполняет присвоение P_v = F(P_v) и возвращает F(P_v). Каждое ребро мы удалим 1 раз, значит суммарно вызов всех функций F(v) работает O(n).

Итоговое время работы O(logx) на запрос первого типа и O(1) в среднем на запрос второго типа.

593E - Странные вычисления и кошки

Научимся решать задачу для маленьких t. Воспользуемся стандартной динамикой dp_x, y, t = количеству способов попасть в клетку (x; y) в момент времени t. Пересчет это сумма по всем допустимым способам попасть в клетку (x; y) в момент времени t – 1.

Заметим, что такую динамику можно считать при помощи возведения матрицы в степень. Заведем матрицу переходов, T_i, j = 1, если мы можем попасть из клетки i в клетку j. Пусть у нас был вектор G, где G_i равно количеству способов попасть в клетку i. Тогда новый вектор G' через dt секунд G' = G * (T^dt).

Таким образом мы научились решать задачу без изменений за O(log dt * S³), где dt — момент времени, S – площадь.

Рассмотрим, что происходит в момент добавления и удаления кота. При таких запросах изменяется матрица переходов. Между этими запросами T постоянная, значит мы можем возводить матрицу в степень. Таким образом, в момент изменения мы пересчитываем T, а между изменениями возводим матрицу в степень.

Решение за O(m * S³ log dt), m – количество запросов

Комментарии (50)

Показать архивные | Написать комментарий?

josdas

9 лет назад, # |

Auto comment: topic has been translated by josdas (original revision, translated revision, compare)

→ Ответить

xozzslip

B — упрощенный случай задачи, разобранной в Кормене гл. 35 "Проверка пересечений". Можно ознакомиться, как такое решается в более общем случае.

Ralsei

← Rev. 4 →

+17

B: There is no need to use eps, if the equal Y1 to sort by Y2(and Y2 by Y1). So all numbers will be int instead of double.

AndrewB330

← Rev. 2 →

B: заполним массив pair<ll,ll> a[n] — у координата каждой прямой в точках x1, x2 соответственно. Сортим наш массив. Теперь достаточно проверить пересекается ли каждая i-ая с i+1-ой. Доказательство: Так как мы отсортировали прямые по какому-то краю, то если 2 прямые с индексами i,j (i<j-1) пересекаются, то любая прямая с индексом k (i<k<j) пересечет одну из данных, таким образом достаточно будет проверить только соседей. Пересекаются ли две прямые будем проверять просто: if (sign(a[i].first-a[i+1].first)*sign(a[i].second-a[i+1].second)<0) ...

I_love_tigersugar

+48

I don't think your solution on E is fast enough :P

How long does it take your solution to run on this test?

HellKitsune

9 лет назад, # ^ |

+15

It seems that on all of their big testcases time makes big jumps and then increases very little for a while. So the logarithm part is almost always 1.

I wrote a solution which passed their tests in 870ms, but worked on my custom testcase with t[0] = 100000, t[1] = 200000, t[2] = 300000 etc. for 18 seconds.

I still managed to pass that testcase in a bit under 3.5 seconds using the fact that we can take modulo once or maximum twice during 20 multiplications in the third loop of the exponentiation. But the constraints are definitely too big for the solution and the testcases are weak =)

But it will be terrible if author's solution can't pass those tests (Eg. the test I posted in my above comment.)

I regret not coding this solution. I should have coded it, locked and tried hacking others with that test. I wonder which verdict I would received. :P

Didn't see your edit when I replied. We came up with the same thing :D

By the way, differences of 65535 are even better than 100000, they lead to more matrix multiplications. Almost all accepted solutions fail such testcases.

sgtlaugh

I can barely pass this case, just in time, 3977 ms :)

14152591

-31

Contest như cl :)

ptnk_1215_panaka_13

-10

Please write in English for everyone to understand. Thank you.

nitishch

Wow, C solution is awesome. And the question too.

ledinhbao

For problem B, I think that there's no need to use EPS. The announced message during the contest maybe lead contestants the wrong ways.

My solution is all using int. In general, a Line Y = a * X + b, because [a, b] are Integers, [X1, X2] are also Integers, so we can sure that [Y1, Y2] are Integers either.

So now you have ([Yi1, Yi2]), sort that array.

Two lines (i, i + 1) are intersected strictly in range(X1, X2) must have a order that Yi1 <= Y(i+1)1 and Yi2 >= Y(i+1)2. Because all lines are distinct, so these pairs are not identical.

Remember to use long long int.

bholagabbar

I can't realize the fact that only the lines yi and yi+1 will intersect, Even after sorting. Any of the lines could intersect. Can you elaborate a little?

movlro

Let me help you.

Let's suppose you have all the lines sorted in Y1 ascending order.

I will refer to the lines as to their Y1 and Y2: Let's suppose we have,in this order,lines [Y11,Y12],[Y21,Y22],[Y31,Y32] and so on.(Therefore Y31>Y21>Y11,etc)

Your question was why we only need to do the process for the consecutive lines,right? Let's suppose that we have no such two consecutive lines.

Therefore,let's suppose lines 3 and 2 don't intersect but 3 and 1 do.That means that we have already checked lines 2 and 1 and they don't intersect,also.

Well then,3 and 1 intersecting means Y31>Y11 and Y32<Y12

Lines 3 and 2 not intersecting means Y31>Y21 and Y32>=Y22.

But that would mean Y12>Y32>=Y22,and Y11<Y21 since that's how we sorted;

That means lines 1 and 2 intersect. But we supposed there are no two consecutive lines to intersect.Contradiction.

That should be it,please message me if you need further help.

BekzhanKassenov

EPS — плохая идея, ведь что-то может пойти совсем не так. Лучше использовать stable_sort.

14067030

Stable sort здесь особо не при чём: какая разница, как сортировать входные прямые (с сохранением порядка При равенстве или без), если они могут быть заданы в любом порядке. Тут дело в верном компораторе, если написать второй компоратор подобным образом, то stable можно будет убрать.

Как раз-таки при таком же втором компараторе и без stable_sort-а не работал первый тест. Сейчас уже не помню почему, я почти засыпал, но оно не работает :)

fractalon

Кстати, на заметку (по поводу оповещения про задачу D): если делить целочисленно на последовательность чисел одно за другим, то ответ от смены порядка деление не меняется.

А что касается B и eps-а, то есть решение поматематичнее — просто при сортировки по y(x1) при пересечении выше считается та прямая, у которой k больше, а при сортировке по y(x2) — та, у которой меньше. Порядок сохраняется таким образом.

nic11

Мне кажется, с eps решение проще доказывается, а вот целочисленное решение писать приятнее

CWD4RKC0D3R

What a hard contest ! :)

The problem D also solvable with LCA and Heavy Light Decomposition. I solved it with this method.

// sorry i posted into russian page

+11

What hard contest ! :)

The problem D also solvable with LCA and Heavy Light Decomposition. I have solved it with this method.

NoTwo

Can you explain your solution please?

← Rev. 6 →

i choose 1. node root of tree. in heavy light the people use segmenttree on nodes.

but in here, i have edges not nodes. then convert edges to nodes. convert the edge, a node which is one of both nodes of edge and more under then other one. (in here i want to tell you make segmenttree on edges. just it)

example :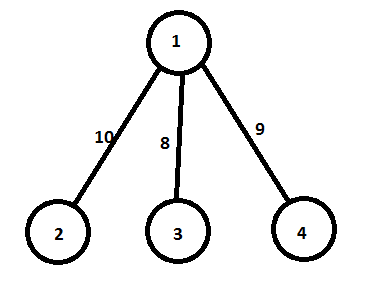

the segmenttree's [2] = 10, [3] = 8 and [4] = 9;

other codes is same as heavy. also to answer queries i find LCA.

i had a problem with overflow. multiply integers with a function which returns 10e18+1 if multiplication bigger than 10e18+1.

saurabhverma

Answered.

kfoozminus

I just solved D with HLD, in this 14087878 — I handled overflow like this —

#define MXN 1000000000000000000LL

long long mrg(long long x, long long y)
{
	if( x * y < x || x * y < y) return MXN + 1LL;

	return x * y;
}

which gave WA at 37. When I replaced this with (14087899)-

#define MXN 1000000000000000000LL

long long mrg(long long x, long long y)
{
	if((x * y)/y != x ) return MXN + 1LL;

	return x * y;
}

AC. Can you please tell me why? If overflow happens, shouldn't (x*y) be smaller than x or y?

no. it doesnt have to be smaller than x or y.

MisakaMisakaMisaka

Computer handle the multiplication overflow by simply cut the higher bits off. So we couldn't make sure that after cutting off the higher bits, x*y will be smaller than x or y.

orz_liuwei

However signed integer overflow is undefined behaviour. Compiler can optimize it aggressively and you can't predict what would happen. To be precise, GCC would assume that there is no overflow of signed integers. So it could optimize expression x * y < x to maybe x > 0 ? (y < 1) : (y > 1) which is more fast.

Replace long long with unsigned long long would work if MisakaMisakaMisaka ' analysis is correct.

Read this for more information.

llyyff

I discuss with my friend about Problem B , then I found three different ways to solve : 1.I adopt which as same as Tutorial. 2.Zhang make a little change with "sort" , just raplace the "x1 += eps , x2 -= eps" : ~~~~~ struct Line{ int yl, yr, k, b; }l[N];

bool cmp(Line a, Line b){ if(a.yl == b.yl) return a.yr < b.yr; return a.yl < b.yl; } ~~~~~ 3.Bao found that if there is a intersection ， then adjacent lines must will make . so just sort , then judge in turn . =_= ...

oversolver

Я начал даже писать точно такое же решение по Е, но открыв калькулятор, у меня получилось полтора миллиарда операций (20^3 * 17 * 10000). Что меня и остановило, но теперь я вижу, что авторское такое же?

mochow

Cannot understand the solution of the problem D properly. :/

Can someone make it simple and explain?

u should know that floor(floor(x/m)/n) = floor(x/mn). Hence u just need a segment tree to maintain the product of a segment. And since we do this on a tree, heavy-light decomposition is needed.

Thanks. This problem is solved by LCA-DSU by many of the other coders. I checked the solution of waterfalls and it was pretty understandable.

AM51

8 лет назад, # ^ |

Can somebody explain the approach used

kshitij1114

but the product will become too big to be stored in any integer datatype. How do I handle that?

you can use (a*b)/b==b to check whether there is overflow. And if there is, just set the product's value as 1e18 or other big value.

dogther

For each node i, we simply maintain fa[i], which means the deepest node on its path to root, whose Rv > 1. For the first type of query, we just walk up through the array fa[] and update the value of y (as other edges are useless) , and we at most walk for 64 times. For the second query, after changing the value of Rv to 1, we need to change fa[v] to its father's fa[] (this node is no longer useful). Just like dsu, we will compress the path while visiting these nodes.

You can have a look at my solution 14098546.

tyamgin

Контест из разряда "Сначала думай, потом пиши". Кучу времени потратил ни на что.

PekpyT

Безусловно, самый лучший вид контестов.

rcg_

What goes on B when we sort Y1 and Y2 in a vector of pairs then check, why do we have to sort them individually ?

loser21

What's the intuition for C ? How do you arrive at such an expression?

zhsh

+14

This is how I came up with my solution.

I ignored all this bla-bla-bla about points being inside or on the border of circles and tried to solve similar problem for points being exactly at the centers of the circles. This condition is stricter than the original one (and might be unsolvable), but if we solve this one, we solve the original one. So I was looking for functions f(t), g(t), such that: f(1) = x[1], g(1) = y[1] f(2) = x[2], g(2) = y[2] ... f(N) = x[N], g(N) = y[N]
Now we can forget that we have 2 different functions f(t) and g(t), and try to solve it only for f(t) and x[1..N]. If we solve it for f(t) and x-coordinates, we will apply the same logic to g(t) and y-coordinates.
The definition and some examples of "correct" functions should tell us that we can generate almost any "saw-looking" function. What is "saw-looking"? Well, not easy to define properly, but here is an example of graph for "abs(5-abs((1-abs(x-1))))-2": https://www.google.com.sg/webhp?ion=1&espv=2&ie=UTF-8#safe=off&q=abs(5-abs((1-abs(x-1))))-2

We can generate a bunch of saw-functions just by changing the coefficients and number of "abs" functions.

Let's forget for now about functions like "x*x" which are also "correct", but these are parabolas, and let's have our fingers crossed we will not need these to solve our problem.

Let's try to represent f(t) as a sum of N "saw-looking" functions. f(t) = f1(t) + f2(t) + ... + fN(t)

Can we find such "saws", that f(1) = x[1], ..., f(N) = x[N]? My first idea was to generate "saws", such that fK(t) = 0 for all t < K. If we can find such saws, we are almost good to solve the problem. I think I saw a solution that implemented this idea, but I gave up during the round and tried to find something else.

What if find magical fK(t), such that fK(K) = x[K], and fK(t) = 0 for all t != K. If we do this, our problem is solved. When we calculate f(t) = f1(t) + ... + fN(t), all numbers fi(t) will be equal to 0 but one. And f(t) will be equal to ft(t), which will be equal to x[t]. Bingo!
Now we need to find magical fK(t). Interesting observation. If we have saw-looking function s(t), we can generate function s(t) + abs(s(t)), which will be a doubled saw if s(t) >= 0, and zero if s(t) < 0. For example, abs(5-abs((1-abs(x-1))))-2 + abs(abs(5-abs((1-abs(x-1))))-2): https://www.google.com.sg/search?q=abs(5-abs((1-abs(x-1))))-2+%2B+abs(abs(5-abs((1-abs(x-1))))-2)&oq=abs(5-abs((1-abs(x-1))))-2+%2B+abs(abs(5-abs((1-abs(x-1))))-2)

That's where the magic happens. If we take a function 1-abs(t-k), and apply this magic transformation, we will get a function that is equal to 2 if t = k, and equal to zero otherwise.

We are almost there! If we define fK(t) = (1-abs(t-K)) + abs((1-abs(t-K))), and slightly adjust a formula for f(t), we will get the following: f(t) = f1(t)*x[1] + f2(t)*x[2] + ... + fN(t)*x[N] f(1) = 2*x[1] ... f(N) = 2*x[N]

What should we do about this "2"? If x[k] is even, we will just divide x[k] by 2 in the definition of f(t): f(t) = f1(t)*x[1]/2 + f2(t)*x[2]/2 + ... + fN(t)*x[N]/2

But what if x[K] is odd?

Oh, we remembered that we were solving a problem with stricter conditions. In the original problem we do not need to generate points at the centers of circles. They can be just close enough to the centers. Checking the problem statement, we see that the minimum radius is 2, but not 1! That's good news. f(t) might be equal to x[t]-1, x[t] or x[t]+1.

This tells us that this definition will work even for odd values: f(t) = f1(t)*x[1]/2 + f2(t)*x[2]/2 + ... + fN(t)*x[N]/2

f(t) will be equal either to x[t] or x[t]-1.

Solved!

The core idea of the solution is the magic function (1-abs(x)) + abs(1-abs(x)). It is equal to 2 if x=0, and is equal to zero otherwise. By shifting it to the left/right, we will generate the basis for our solution.

MayankPratap

In DIV2 B , sorting vector<pair<double,double> > gives TLE while vector<pair<long long,long long> > gives AC ... Can someone explain why this is happening?

← Rev. 3 →

Because use scanf() or sync_with_stdio(false). Read the 10^5 double numbers is quite long.

http://codeforces.net/contest/593/submission/14093632

By the way, you have a bag with for(int i = 0; i < n; i++), because when you use v[i + 1] you get vector index out of bounds, but i have no idea why you passed test 8, and my resubmite don't.

http://codeforces.net/contest/593/submission/14093538

P.S. So many local variables...

dothanhlam97

http://codeforces.net/contest/593/submission/14179073

Problem D I don't know Why I have a wrong answer on test 15. I have found the mistake for 3 days but I can't :( Help me :(((

I used heavy light decomposition.

Akemi__Homura

Why I always get TLE of problem D Happy Tree Party in Test 13?