Here's my understanding of the solution provided in your link:

A sufficiently 'nice' sum that depends only on N will be a polynomial on N. I don't have a definition of 'nice' or a proof that this sum is 'nice', but several examples should convince you of this —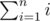 or or .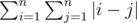

Furthermore, the degree of the polynomial should be 10. We're multiplying five terms and summing over five variables. Again, take a look at the above examples — the third one should be a degree-three polynomial in N, as we are multiplying one term and summing over two variables.

Unfortunately, we don't know the coefficients of this magical 10th degree polynomial. However, we can find them if we have 10 linear equations in terms of these coefficients. Let P(N) = c₁₀x¹⁰ + ... + c₁x + c₀. Then our desired equations are P(N_i) = c₁₀(N_i)¹⁰ + ... + c₁N_i + c₀ for 10 different N_i, where P(N_i) must be calculated manually or with a slow program.

Finally, we put these equations into an augmented matrix and use Gaussian elimination to solve for the 'variables', which are the 10 coefficients c_i. Now we simply evaluate P(N) for each given N.