нет

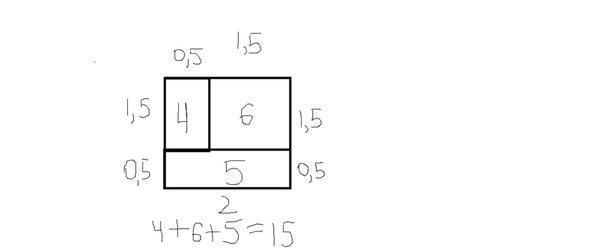Жюри ответило,что размеры комнат должны иметь целыми.

1) Можно посчитать частичные xor на префиксе, тогда xor на отрезке это p[r]^p[l-1].

2) Отсортируем позиции в массиве по возрастанию чисел, на них стоящих. На i-ом шаге добавим i по возрастанию позицию. Чем мы можем срелаксировать ответ? Каким-нибудь отрезком, который уже полностью добавлен и содержит i. Максимум на нем равен a[i].

3) На каждой итерации работы алгоритма добавленные элементы образуют множество отрезков. Для каждого отрезка будем поддерживать битовый бор из частичных ксоров, входящих в него элементов. В этом боре мы просто храним битовые записи чисел как строки. Также этот бор умеет максимизировать ксор какого-то числа с числами в него положенными(просто жадно идём по лучшему ребру).

4) Когда мы добавляем новое число, оно образует новый отрезок. Кроме того, некоторые отрезки надо объединить. Когда объединяем отрезки будем кидать числа из одного бора в другой, параллельно обновляя ответ максимальным ксором, умноженным на текущий элемент. Это решение все ещё работает за квадрат.

5) Хитрость: будем всегда приливать из меньшего бора в больший. Тогда общее количество перекладываний O(nlogn).

Итого решение за O(n logn log10^6)

Мы решали персистентым бором. #10536760

авторское решение было мит ин зе мидл. для сливания использовался битовый бор, в котором хранятся все числа в правой части отрезка, в левой перебираем элементы, которые мы возьмем и в боре находим максимальный хор. это решение так же было за NlogNlog10⁶

tl;dr: в коде чекера написано примерно так:

string answer = ...;
string output = ...;

if ((answer != output) && output == "NO") {
    return WA;
}

if (output == "YES") {
    if (!check_certificate()) {
        return WA;
    }
    assert(answer == "YES");
}
return OK;

Мы чекали каждую длину. На анаграммы проверяли по частичным суммам пар <сумма квадратов, сумма корней>.

Пусть q1 — очередь из монстров, которые в данный момент стоят в очереди за билетами, q2 — очередь из тех монстров, которые еще не пришли к данному моменту, q — сет из монстров, в котором ключ — пара(t[i] % k, i), которые приходят не позже какого-то момента времени, но еще не в q1. В очереди все расположены по неубыванию t[i]. Тогда, достанем следующего чувака из очереди q2, пусть он приходит в момент времени tcur. Удалим из первой очереди всех, у кого время ухода из магазина не позже, теперь, если в очереди q1 меньше, чем m чуваков, пересчитаем для текущего ответ(как максимум из времени выхода последнего монстра из первой очереди плюс h[i]), и удалим из второй очереди его(и из сета, если он там есть), и добавим в первую. Если в первой очереди есть m чуваков, которые уходят позже tcur, тогда поймем, какого чувака мы хотим взять сейчас. Пусть T — время ухода первого монстра из q1. Во-первых, для монстра, который зайдем в q1 следующим, должно быть выполнено t[i] < T + k, так как чувак со временем tcur придет раньше этого момента времени. Тогда монстр, который будет приходить в моменты t[i], t[i] + k, ..., t[i] + j * k, сможет войти в очередь q1 в момент времени T + (t[i] — T) % k. Нам нужно найти минимальный момент времени, то есть нам нужно найти монстра, у которого t[i] < T + k, и остаток от деления на k как можно ближе к T, для этого нам и понадобится сет q, в котором будут находиться только монстры с t[i] < T + k. Добавим из q2 в сет всех монстров с таким условием на время прихода, при этом не удаляя их из q2. Найдем в сете с помощью lower_bound ближайший к T % k элемент, если такого не нашлось, то возьмем минимальный. Далее удалим из сета и второй очереди этот элемент и добавим в первую.

Не извиняйся брат, не извиняйся.

Начнем получать из строки s пустую строку. Состояние, в котором мы сейчас находимся, описывается двумя числами — это кратность символов, которые образуют текущую строку, и кол-во их с начала строки. (для строки abcdefgh k = 2, p = 3 задает, ace, 0-й символ, 2-й символ, 4-й символ, всего 3 символа с начала строки), всего таких состояний nlogn (это sum(n/i), по i=1..n).

Построим граф таких состояний (k, p) и будем искать кратчайший путь в нем bfs. У нас два варианта:

1) Строка получена конкатенацией, тогда идем с конца по по строке и проверяем наличе такого суффикса в боре (бор из перевернутых строк a[i]), и проверяем, если попали в терминальную вершину, то переходим в (k, p-lev) (lev — глубина этой терминальной вершины, т.е. длина a[i]). Эта часть решения работает за nlogn * MAXLEN(a_i)

2) Строка получена умножением, тогда перберем делитель d числа p, и проверим, что строка могла быть умножена на какую-то a[i] с помощью хешей или z-функции, и перейдем в новое состояние (d*k, k*p/d). На самом деле, именно перебирать вот так d, как делитель p — долго, быстрее будет сделать следущий предподсчет: фиксируем k, перебираем j, увеличиваем длину p, и проверяем, что можно перейти из (k, p)->(k*j, p/j), по ходу увеличения длины p проверяем хэшами (либо z-функцией), что действительно этот переход получен умножением. этот предподсчет занимает около 7млн операций при таких ограничениях.

на самом деле можно было решать задачу дп, а не бфсом, но основная идея все та же: состояние задается парой (k, p) — (кратность символов, и количество их с начала).

Решение простое: сначала разобьем вершины на два множества случайным образом. После этого будем повторять следующую операцию: возьмем вершину, у которой все плохо — количество исходящих из нее ребер в ее компоненту больше, чем в другую. Эту вершину просто перенесем в другое множество.

Процесс конечен, так как после каждого переноса уменьшается количество ребер между двумя множествами. А это значит, что когда-нибудь "плохих" вершин не останется, и все будет хорошо. Победа.

Переносов может быть не более O(E), каждый из них делается за O(V). Итого решение за O(VE).