A div2. В этой задаче можно было промоделировать весь процесс. А именно - рассматривать все минуты подряд и, в зависимости от того, какого цвета в данную минуту подошла кабинка, уменьшать соответствующую группу студентов G на min(|G|, 2), где |G| - размер группы. После этого нужно определить самую первую по счету минуту t, в которую все три группы опустеют. Тогда t + 30 будет ответом. Это решение за O(r + g + b).

Также в этой задаче есть решение за O(1). Оно выражается следующей формулой: ans = max(3[(R + 1) / 2] + 27, 3[(G + 1) / 2] + 28, 3[(B + 1) / 2] + 29), где [x] --- округление вниз до ближайшего целого.

B div2. Задачу можно было решить реализовав ровно то, что написано в условии. А именно: для каждой буквы просмотреть все буквы в той же горизонтали и в той же вертикали, что и данная буква. Если найдется такая же - эту букву выводить не следует. Сканирование и вывод ответа можно было совместить, например, так:

FOR(a,1,n) FOR(b,1,m)
{
    bool should_out=true;
    FOR(c,1,n) if (c!=a) if (T[a][b]==T[c][b]) should_out=false;
    FOR(c,1,m) if (c!=b) if (T[a][b]==T[a][c]) should_out=false;
    if (should_out) printf("%c", T[a][b]);
}

Данное решение работает за O(mn(n + m)).

Также есть решение за O(nm). Для каждой строки и столбца можно посчитать количество в ней каждой из букв алфавита. После этого проверку на то, что букву слудует выводить, можно выполнить за O(1). Для этого надо проверить что в соответствующих стоке и столбце количество вхождений соответствующей буквы равно 1.

C div2 и A div1. Определим какой вид имеют всевозможные расположения алмазов такие, что множество сумм всех пар ячеек остается неизменным. Если мы из первой ячейки уберем некоторое количество c алмазов, то во вторую ячейку на надо будет добавить c алмазов, из третьей убрать c алмазов и так далее. Другими словами, все валидные положения алмазов получаются, если мы во всем четным ячейкам добавим ровно c алмазов, а из всех нечетных ровно c уберем, где c - некоторое целое число. 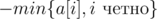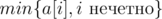c находится в пределах от до , поскольку иначе в некоторых ячейках получится отрицательное количетсво алмазов. Других валидных расположений нет.

Теперь посмотрим как будет меняться сумма всех алмазов с изменением c. Если n четно, то сумма никогда не меняется, украсть что либо невозможно и ответ --- 0. Если n нечетно, то при некотором фиксированном c ровно c алмазов остаются лишними. Таким образом, Джо может украсть не более 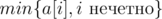алмазов.

Нетрудно понять, что для того, чтобы увеличить (или уменьшить) c на некоторую константу x, требуется x[((n + 1) / 2)] перемещений, причем меньшам количеством обойтись нельзя. Таким образом, за минуту Джо может изменить c на не более чем [m / ((n + 1) / 2)]. Общее количество алмазов, которое может похитить Джо за все время равно k[m / ((n + 1) / 2)], однако тут следует учесть ограничение на изменение c.

Итого, решение получается следующим: Если n четно, то ответ --- 0, иначе ответ .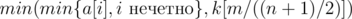

В задаче нужно было быть аккуратным с переполнением 32битного типа и использовать 64битные типы.

D div2 и B div1. Можно было построить мультиграф, в котором вершинами являются виджеты, а ребрами --- отношение вложенности виджетов. Из условия следует, что этот граф ацикличен. Далее на нем нужно было сделать топологическую сортировку вершин и в полученном порядке для всех вершин пересчитать размеры соответствующего виджета. Ну и не забыть вывести ответ.

О реализации.

Распарсить инструкции удобнее всего было следующим образом: заменить все символы '.', ',', '(', ')' на пробелы и разбить инструкции на последовательность строк, где пробелы, собственно, являются разделителями. После этого разбор выражений проходит просто.

Хранить мультиграф можно было в виде целочисленной матрицы смежности, где число M[i][j] обозначает количество ребер из вершины i в вершину j. Топсорт можно было делать даже самым тупым алгоритмом, например, таким: k раз за O(k²) (k --- количество вершин в мультиграфе) искать вершину, из которой не исходит ребер в еще не выбранные вершины.

Пересчитывать размеры следовало в 64 битных числах (об этом даже была подсказка в условии). В тесте вида

100
Widget w(100,100)
HBox box
box.pack(w)
box.set_border(100)
HBox a
a.pack(box)
a.pack(box)
HBox b
b.pack(a)
b.pack(a)
HBox c
c.pack(b)
c.pack(b)
...

ширина виджета растет экспоненциально. Самая большая ширина виджета в тестах жюри равна 103079215104000. Ее можно получить если каждый раз упаковывать в один виджет не 2, а сразу 4.

E div2 и C div1. Задачу можно было решить с помощью моделирования. Просто перебираем все фишки и для каждой из них считаем количество очков. Однако моделирование в лоб в худшем случае дает решение за время O(k³), где k --- количество фишек, что не укладывается в ограничения по времени. Например, на таком тесте:

1 5000
RRRR...[2500 раз]LLLL...[2500 раз]

Можно было моделировазь за время 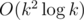, но это тоже не проходит в ограничения.

Моделирования за O(k²) дает следующая структура данных.

Для каждой фишки будем хранить указатель на ближайшие фишки слева, справа, сверху и снизу. В самом начале построить сеть указателей можно за время O(nm). Далее, в процессе моделирования, удалять вершины можно было следующим образом:

Chip->L->R = Chip->R
Chip->R->L = Chip->L
Chip->U->D = Chip->D
Chip->D->U = Chip->U

Таким образом, переход к каждой следующей фишке в процессе хода выполняется за O(1). Каждый ход моделируется за время O(k).

Операции удаления обратимы (ведь у удаленной фишки остались указатели на соседей). Поэтому в процессе хода нужно сохранить ссылки на все удаленные фишки, а затем в обратном порядке выполнить

Chip->L->R = Chip
Chip->R->L = Chip
Chip->U->D = Chip
Chip->D->U = Chip

Впрочем, можно было перед проверкой очередного хода игрока строить сеть ссылок заново.

D div1. Сначала раздуем все мины на радиус Звезды Смерти, а саму Звезду Смерти сожмем до точки. Тогда нам нужно определить пересекает ли луч полученные фигуры.

Тело мины радиуса r при раздувании переходит в шар радиуса r + R. Каждый шип мины после раздутия превращается в объединение двух шаров радиуса R и цилиндра. Один из этих шаров всегда находится внутри раздутого тела мины, поэтому его можно далее не рассматривать. Пусть длина шипа r₀. Тогда цилиндр будет иметь высоту r₀ и радиус R, расстояния от центра одного из оснований до края другого равно 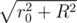. Следующее неравенство показывает, что это расстояние всегда меньше радиуса раздутого шара, то есть цилиндр лежит внутри раздутого шара: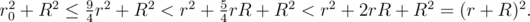



Таким образом, цалиндры тоже можно не рассматривать. От раздутых шипов остаются только шары радиуса R с центрами в кончиках шипов.

Итак, у нас есть множество шаров различного радиуса, нужно определить как быстро с каждым из них столкнется точка и из всех таких времен выбрать минимум (если точек пересечения нет, то следует вывести). Запишем уравнение:

|A + vt - O| = R,

где A --- начало движения точки, v --- вектор ее скорость, O --- центр шара, R --- его радиус. Перепишем все в скалярных величинах:

(A_x + v_xt - O_x)² + (A_y + v_yt - O_y)² + (A_z + v_zt - O_z)² = R².

Раскрыв скобки, получим квадратное уравнение относительно t:

At² + Bt + C = 0.

Решаем его обычным методом, выбираем наименьший корень (меньший корень --- это время вхождения точки в шар, а больший --- время выхода). Проверяем, что корень больше 0 (поскольку у нас пересечение луча с шаром, а не прямой).

Ограничения на координаты были таковы, что все вычисления можно было сделать в целых 64битных числах с абсолютной точностью.

E div1. Все что может делать Соломон --- это создавать некоторые отрезки из ледяных кубиков, а затем отрезать их. Рассмотри один из отрезков, начало которого начинается правее всего. Без ограничения общности, можно считать, что данный отрезок всегда заканчивается в позиции последнего демона (иначе всегда можно переклеить к нему хвост отрезка, что кончается правее его). Понятно, что чтобы его отрезать, всегда нужно построить к нему "мостик" из ледяных блоков, а затем отрезать. В процессе построения этого мостика будем сразу же строить и отрезать все остальные отрезки.

Теперь будем перебирать все возможные положения начала последнего отрезка. Для каждого фиксированного последнего отрезка уменьшим силы демонов, которые он покрывает и определим минимальное количество операций, за которые мы накроем все отрезки (включая последний!).

Заметим, что на каждый упавший кубик приходится ровно 3 операции --- пройти вправо, создать и пройти влево, а на каждое отрезание отрезка приходится ровно 2 операции --- создание кубика и его уничтожение. Поэтому всех демонов (с учетом их силы) следует покрыть наименьшим числом отрезков так, чтобы зря не упало ни одного кубика. Это можно делать жадно.

Количество, операций, необходимое для покрытия всех демонов с учетом их силы для фиксированного последнего отрезка можно вычислить за O(n). Поскольку проверок не более O(n), получаем решение за O(n²).

Ответ в конце восстановить несложно.