Hello everyone
I am facing the following geometry problem, and since am not so good at it, i would ask your help:
We have a straight line that goes throw 3 points, A(X1,Y1) B(X2,Y2) and M(X0,Y0).
We know X1,Y1,X2,Y2 and we know d, the distance between A and M, and we have to define the two possible positions of the pair X0,Y0...
Any Help would be highly appreciated, and thanks in advance...











Here is
O(1)solution with some inaccuracy permitted:You know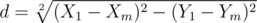
You also know slope of line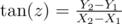
So, the two possible values of Xm are X1 ± d * cos(z)
Similarly, Ym = Y1 ± d * sin(z)
You can explain little more pls.....
from the image you can say that sin(z)= (y0-y1) / d from this equation you can say that sin(z)*d = y0-y1 so: y0 = y1 + d*sin(z) but y0 may also be in the other direction so y0=y1(+or-)d*sin(z) also you can notice that cos(z)=(x0-x1)/d from this you can say that x0=x1(+or-)d*cos(z) and you can calculate z since that tan(z)=slope which equals to (y2-y1) / (x2-x1) you can make tan inverse to get z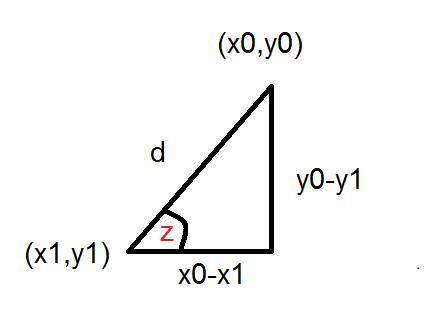
thanks
.