kofhearts's blog

understanding factorization method. help!
By kofhearts, history, 9 years ago, In English

hello codeforces,

I am trying to understand the reason why only up to sqrt of n numbers are checked for factors. There is a maths theorem that if a number is not prime then it should have at least 1 factor which is less than sqrt(n). Is the following routine using that fact. My understanding is that in each iteration it is trying to find at least 1 such factor less than sqrt of n and once it finds it then the new n is updated to n / factor. This will give a new n and the same procedure is applied i.e another small factor is tried to be found in the range till sqrt of n. Please give me a better explanation if there is an easier way to understand why we just need to search till sqrt(n) for the factors. I appreciate it! Thanks!


def primes(n):
    primfac = []
    d = 2
    while d*d <= n:
        while (n % d) == 0:
            primfac.append(d)  # supposing you want multiple factors repeated
            n //= d
        d += 1
    if n > 1:
       primfac.append(n)
    return primfac
  • Vote: I like it
  • +6
  • Vote: I do not like it

Comments Comments (2)
| Write comment?
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

lets call the number you want to decompose X

Ok, so what the math theorem says is that :

Either X is prime . or In case X is composite ===> It has a prime divisor that is less_than_or_equal to SQRT(X)

Why is that?

Suppose X is NOT prime , it means that X got At least 2 prime divisors . For example 26 is not prime , The prime divisors of 26 are 2 and 13 because 2*13=26

Ok now lets list all the prime Divisiors of number X. let the list be P1,P2,P3...Pn

We will prove by contradiction that at least 1 of the numbers P1,P2...Pn is less than SQRT(X)

Suppose all P1,P2,P3...Pn are strictly GREATER than Sqrt(X);

now X can be written as X=SQRT(X)*SQRT(X)

The contradiction results from the fact than if you multiply At LEAST 2 numbers , be P1,P2 that are greater than SQRT(X) you will get a number that is greater than X;

Therefore if number X is not Prime , it will ALWAYS have At Least 1 prime divisor that is less than_or_equal to SQRT (X)

So you can iterate from 2 to SQRT(X) and look for divisors , in case you find one Divide X by the prime number and repeat the procedure;

if you don't find any divisor in the range 2...SQRT(X) that means the number is PRIME for sure.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Well, if you think about it, it's quite obvious. A divisor d of a number n is either n itself or n divided by another divisor d'. If we ha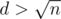d and 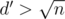, then we would have 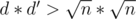, that is d * d' > n, which is a contradiction. This means that we can find all divisors by trying only numbers .

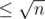→ Reply