612A - The Text Splitting

Переберём количество строк длины p и q в ответе. Пусть это величины a и b. Если a·p + b·q = n, то посторим ответ, откусив с префикса сначала a раз строки длины p, а затем b раз строки длины q. Если ни одной подходящей пары a, b не нашлось, то ответа не существует. Конечно эту задачу можно решать и за линейное время, но здесь это не требовалось, поскольку ограничение на длину строки было маленьким.

Асимптотическая сложность решения: O(n²).

612B - HDD is Outdated Technology

В условии задачи задана перестановка f. Построим по ней другую перестановку p следующим образом: p_fi = i. Таким образом, перестановка p определяет номер сектора по номеру фрагмента. Перестановка p называется обратной к перестановке f и обозначается f^- 1. Теперь ответ на задачу равен просто .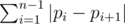

Асимптотическая сложность решения: O(n).

612C - Replace To Make Regular Bracket Sequence

Заметим, что поскольку мы не можем менять тип скобок, то для существования ответа необходимо, чтобы заданная строка была правильной скобочной последовательностью без учета вида скобок. Если это не так, то ответа не существует. Иначе каждой открывающей скобке соответствует ровно одна закрывающая, и каждой закрывающей — ровно одна открывающаяя. Теперь заметим, что если пара соответствующих друг другу скобок одного вида, то их мы можем не менять. Если же они разного вида, то поменяем вид закрывающей на вид открывающей. Таким образом, мы построим ответ. Легко убедиться, что ответ оптимальный, поскольку задачи для несоответствующих друг другу скобок не связаны друг с другом и могут быть рассмотрены по отдельности.

Единственная техническая тонкость в том как найти соответствующие друг другу скобки. Для этого заведем стек открытых скобок. Теперь будем идти по строке слева направо и если скобка открывающая, то просто добавим ее в стек. Если же она закрывающая, то возникает три случая: 1) стек пуст; 2) вверху стека лежит открывающая скобка того же вида, что и текущая закрывающая; 3) вверху стека скобка вида отличного от текущего. В первом случае ответа не существует, во втором нужно просто выкинуть открывающую скобку из стека, а в третьем нужно выкинуть открывающую скобку из стека и увеличить ответ на единицу.

Асимптотическая сложность решения: O(n).

612D - The Union of k-Segments

Для каждого отрезка создадим два события в момент l_i — открытие отрезка и в момент r_i — закрытие отрезка. Отсортируем все события по моменту времени, при равенстве сначала будем обрабатывать события открытия отрезков. Это можно сделать, например, накидав в vector<pair<int, int>> events (пример для языка C++) пары момент времени и тип события ( - 1 для открытия и  + 1 для закрытия). Далее это массив можно отсортировать стандартным компаратором.

Теперь будем идти по массиву events и считать баланс отрезков balance, для этого каждый раз нужно просто из баланса вычесть тип события. Теперь если баланс оказался равен k, а до этого был k - 1 значит мы стоим в левом конце отрезка из ответа, запомним этот левый конец (равный моменту текущего события) в переменную left и будем идти дальше. Если баланс оказался равен k - 1, а до этого был равен k значит мы обнаружили конец некоторого отрезка из ответа right. Добавим в ответ отрезок [left, right]. Таким образом, мы получим непересекающийся набор отрезков, содержащий все покрытые точки, в порядке слева направо. Очевидно он и является ответом на задачу.

Асимптотическая сложность решения: O(nlogn).

612E - Square Root of Permutation

Рассмотрим некоторую перестанову q. Построим по ней ориентированный граф дугами, которого будут (i, q_i). Этот граф, как известно, представляет собой набор неперескающихся циклов. Теперь посмотрим, что происходит с этим графом при возведениии перестановки в квадрат: все циклы нечетной длины остаются таковыми (только порядок вершин меняется, происходит чередование через одну вершину), а циклы четной длины разбиваются на два цикла вдвое меньшей длины. Таким образом, чтобы найти корень из перестановки нужно оставить все циклы нечетный длины, прочередовав их в обратном от возведения в квадрат порядке, а циклы четной одинаковой длины нужно разбить на пары и слить в один цикл (если оказывается невозможным разбиение на пары, то ответа не существует).

Асимптотическая сложность решения: O(n).

612F - Simba on the Circle

Авторское решение по этой задаче основано на динамическом программировании. На мой взгляд никакие жадные идеи в этой задаче не работают. Для решения задачи будем считать две динамики z1_i — ответ на задачу если все числа меньшие a_i уже выведены, а больше либо равные еще нет; и z2_i — ответ на задачу если все числа меньше либо равные a_i уже выведены, а большие еще нет. Введем обозначение d_ij — кратчайшее расстояние от i до j на кольце и od_ij — расстояние от i до j если идти по часовой стрелке. Легко видеть, что z2_i = min_j(z_j + d_ij), по всем j таким, что a_j есть наименьшее число большее a_i. Пусть теперь хотим посчитать значение z1_i. Рассмотрим все элементы равные a_i (в одном из них мы сейчас находимся). Если такой элементв один, то z1_i = z2_i. Иначе у нас есть два варианта обхода этих элементов: по или против часовой стрелки. Пусть мы идём по часовой стрелке, тогда последним мы выпишем число из ближайшего к i равный элемент против часов стрелке, пусть это элемент u. Иначе последним мы последним посетим ближайший к i элемент по часовой стрелке, пусть это элемент v. Тогда z1_i = min(z2_u + od_iu, z2_v + od_vi). Теперь легко видеть, что ответ на задачу равен min_i(z1_i + d_si), по всем i таким, что a_i есть наименьший элемент в массиве, а s есть стартовая позиция. Плюс к этому ко всему как усложнение в задаче нужно было восстановить ответ. В этих случаях, на мой взгляд, проще всего написать рекурсивную реализацию динамики (хорошо протестировать её на работоспособность), затем скопировать всю динамику на восстановление ответа (для деталей выкладываю свой код). Конечно это можно делать и без копипасты, например, передавая в динамику булеву величину нужно ли восстанавливать ответ.

Асимптотическая сложность решения: O(n²).

Code