adamant's blog

On suffix automaton (and tree)
By adamant, history, 9 years ago, translation, In English

Hi everyone!

This summer in Moscow IPT was held Moscow International Workshop ACM ICPC. I gave a lecture on suffix structures there (it was only about suffix automaton and suffix tree actually). In this regard, I would like to present to you the lecture notes. So here are Russian and English versions. Enjoy and Happy Holidays :)

P. S. My very apologies for my bad English :(

UPD: Thanks to Burunduk1 for help in code formatting.

UPD2: Please also refer to Wikipedia article on this topic. I'm the main author of its current (29 Oct 2021) version.

  • Vote: I like it
  • +209
  • Vote: I do not like it

Comments Comments (11)
| Write comment?
»
9 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Hi, first of all thanks a lot, and secondly would you mind tagging this with tutorial so it would be easier to search for in the future? I looked at the notes, and they are definitely not to be missed out on!

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I was reading your excellent tutorial and got confused by one sentence(paragraph). Could you plz explain it to me?

Pretty easy to understand that in case of suffix automaton right conext X(a) of string a has mutual correspondence with the set of right positions of occurrences of the string a in the string s. Indeed, if ax is accepted by automaton, that is, it is a suffix of s, then s = yax, and the string x can be matched with position |s| − |x| − 1. Thus, each state of the automaton accepts strings with the same set of right positions of occurrences in s and vice versa all strings with such set of positions is accepted by this state.

I couldn't understand the first sentence clearly. Thanks for helping.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    To each element in right conext you can associate the occurence in string. And vice versa.

    For example, let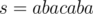 . We can find that 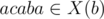and associate it with first occurence of ab ( ab acaba). And for second occurence there is element in right context: 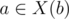(abac ab a).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I understand the example and sort of getting your idea, but what does "mutual correspondence" mean?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It means bijection :)

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          do I need to work more on this paragraph if I can understand your example but not really for the text?

          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Maybe no. Try going on without it and return to it if you have some difficulties maybe

            → Reply
»
3 years ago, # |
  Vote: I like it +29 Vote: I do not like it

Hi everyone! I'm sorry that Google Drive links got broken. I've updated this entry with new links which should work now. On a side note, these lecture notes are quite old and might be somewhat messy, therefore I strongly encourage to use Wikipedia article on this topic. I am the main author of its current version.

--

Всем привет! Извиняюсь, что ссылки на Google Drive сломались. Я обновил пост и добавил работающие ссылки. Тем временем, хочу отметить, что материал тут довольно старый и местами трудный к восприятию, поэтому я предлагаю также ознакомиться со статьёй на Википедии по этой теме. Я -- основной автор текущей версии статьи.

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Ссылка на википедию в посте тоже сломана.

    → Reply