svg_af's blog

Help with 2D segment tree
By svg_af, history, 9 years ago, In English

Hello there

I'm trying to solve this problem

So i was thinking if i create a segment tree where each node has a segment tree that would do the trick

I've heard about 2D segment tree before but never implemented it

the only way i could think off would definitely get me MLE where i do an array seg[n*2][n*2]

if anybody has any tricks that could save memory or maybe the correct way for creatin a 2D segment tree that would be really appreciated :D

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +6 Vote: I do not like it

You can build segment tree, where in each node you have a treap. It will be O(n * logn) memory.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Got any resources i can read from about treaps ?

    kind of a new concept to me

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      link from Wikipedia

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      I've written a range tree of treaps for this problem. Unfortunately it timed out on spoj Here's the code http://codepad.org/Zy7elORD

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        your code will be very helpful to me in learning treaps thank you!!

        i tried implementing and AVL tree in every node of a range tree but it timed out also ... i feel your pain

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      If you find treaps hard to understand, try more easy approach: Balanced Binary search Trees (AVL, Red Black)

      This class of data structures are fit requirements in this problem (treap is also kind of balanced BST, but more complex and powerful). So they can do insert\delete queries in log time, as well as count (number of elements >= KEY).

      You can think in the way that in every node of segment tree you have a set, that can answer the second query.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I understand that and i tried implementing an AVL tree in every node of a segment tree but unfortunately it TLEd

        if you have solved this problem and it's too much trouble here's my code ... what am i doing thats too slow ?

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      This and This

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        thank you they were very helpful

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Also you can use sqrt-decomposition with Fenwick tree. All what you need is to divide the array into parts of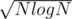 and for every part maintains amount of every number (in fenwick tree). Then every modify query will be processed in O(log(N)), k-query in .

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

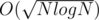    i've heard of sqrt decomposition but never tried it

    guess now is a good chance while trying to implement your solution

    → Reply
»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

If you still want to use 2-D segment tree, you can store in every node Dynamic segment tree.

The key idea is that you don't have to keep all the nodes of segment tree (which is stored in node I mean). You can dynamically create it as soon as you need it.

That is require O(n * log(n) * log(M))

Little example: '[1-4]=0 [1-2] [1] [2] [3-4] [3] [4] ' here is segment tree for 4 nodes. '=0' — indicates the vertex that was created already, and stored the value 0. So if vertex wasn't created means that there is no value in it ==> 0 there. let's make update query: add to +1 to 4-th, then the tree are gonna look like the following:


[1-4]=1
  [1-2]
    [1]
    [2]
  [3-4]=1
    [3]
    [4]=1

Let's provide query how much elements >= 2 in our Data structure. In our case is simply sum over segment [2..4]


[1-4]=1 1) go left son, 3) go to right son, 5) return 0 + 1 = 1
  [1-2] 2) come to left son, realized that it was not created, so return 0
    [1]
    [2]
  [3-4]=1 4) return 1
    [3]
    [4]=1

Hope it make sense.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    it makes so much sense :D

    that was exactly what i needed thank you !!!

    → Reply