sore_loser's blog

Help with FBH round 2 problem C
By sore_loser, history, 9 years ago, In English

I need some help with this problem

Snakes and Ladders

Actually, I think I have got quite a hold of it. What I can't get my head around is as there may be n(n-1)/2 possible pairs at the max, how can I take all these possible pairs in less than O(N^2) time? The constraints clearly mean that O(N^2) won't do. Or is there some way to bypass this calculation? (which I am quite sure there isn't)

  • Vote: I like it
  • -3
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Actually you can do this calculation in O(N) time. Suppose you have N=4 values: x1, x2, x3, x4

So what you gotta find is: (x1-x2)^2+(x1-x3)^2+(x1-x4)^2+(x2-x3)^2+(x2-x4)^2+(x3-x4)^2

this suffices to: 3(x1^2+x2^2+x3^2+x4^2)-2(x1*x2+x1*x3+x1*x4+x2*x3+x2*x4+x3*x4)

the first part is easy to calculate and will take O(N) time. Lets see how the 2nd part (inside the bracket) can be rearranged.

x1*x2+x1*x3+x1*x4+x2*x3+x2*x4+x3*x4=x1*(x2+x3+x4)+x2*(x3+x4)+x3*(x4)

so you can precalculate x1+x2+x3+x4 and then for each xi you will subtract it from the precalculated value before multiplying with it. Whole process can be done O(N) times this way

Hope you got the hang of it.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it +9 Vote: I do not like it

    A bit simpler way is to express

    In general case, the formula will be

    . Now it is obvious how to calculate it in $O(n)$.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Wow, Zlobober . Thats more elegant. I spent 2 hours trying to figure out how to do that in O(N) and after coming up with my solution I had a hunch there must be another easier way. Thanks for the tip :)

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it +3 Vote: I do not like it

        This is a common method of calculating symmetric polynomials in O(n) since each symmetric polynomial can be expressed through power sum symmetric polynomials. Try to calculate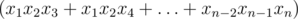 in similar way as an exercise.

        Also, this is an easy way to derive an inequality between arithmetic mean and quadratic mean:

        This inequality holds exactly because we started from the sum of squared pairwise differences that is non-negative.

        → Reply