622A - Бесконечная последовательность
Вычтем из числа n единицу. Определим сначала номер блока в который попало n-е число. Для это сначала вычтем из числа n число 1, затем 2, затем 3 и так далее пока n не станет отрицательным. Количество вычитаний и будем номером блока, а позицией в блоке будет последнее неотрицательное число, которое мы встретим.
Сложность: 
.
622B - Время
В этой задаче можно было a раз прибавлять к текущему времени по одной минуте, аккуратно обрабатывая переполнения часов и минут.
А можно было просто посчитать ответ формулой: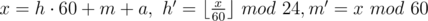 
.
Сложность: O(a) or O(1).
622C - Не равный на отрезке
Задача является значительно упрощённой версией задачи предложенной Mohammad Nematollahi Deemo.
Эту задачу можно было решать по разному, например, с помощью структур данных или sqrt-декомпозиции. Но это, конечно, делать не требовалось. Мы предполагали следующее простое линейное решение. Сделаем сначала предподсчет: для каждого числа номер первого не равного ему слева. Теперь, чтобы ответить на запрос нужно сначала проверить число в правой границе на равентсво числу x, если они не равны то мы уже нашли ответ. Если же они равны проверим первое число слева не равное числу в правой границе.
Сложность: O(n).
622D - Оптимальное расположение чисел
Задача предложена Aleksa Plavsic allllekssssa.
Давайте построим ответ в котором сумма будет равна 0. Пусть n чётно. Давайте расставим нечётные числа в первой половине массива: число 1 в позициях 1 и n, число 3 позициях 2 и n - 1 и так далее. Аналогично давайте расставим чётные числа во второй половине массива: число 2 в позициях n + 1 и 2n - 1, число 4 в позициях n + 2 и 2n - 2 и так далее. Число n мы можем поставить в оставшихся в конце свободных позициях. По аналогии ответ строится для нечётного n.
Легко видеть, что при данном построении искомая сумма равна 0.
Сложность: O(n).
622E - Муравьи в листьях
Задача предложена Aleksa Plavsic allllekssssa.
Легко видеть, что ответ равен максимуму из ответов по сыновьям корня плюс один. Теперь давайте решать задачу отдельно для каждого сына v корня. Пусть z — массив глубин всех листьев в поддереве вершины v. Отсортируем z. Утверждение 1: листья выгодно поднимать в вершину v в порядке сортировки в массиве z. Утверждение 2: обозначим ax — время попадания x-го листа в вершину v и рассмотрим листья zi и zi + 1, тогда azi + 1 ≥ azi + 1. Утверждение 3: azi + 1 = max(dzi + 1, azi + 1), где dx — глубина листа x в поддереве вершины v. Последнее утверждение даём нам решение задачи: нужно просто итерироваться по массиву z слева направо и пересчитывать массив a согласно формуле из утверждения 3. Все три утверждения легко доказать и это предлагается сделать самостоятельно, чтобы лучше понять как решение работает.
Сложность: O(nlogn).
622F - Сумма k-x степеней
Задача предложена Иваном Поповичем NVAL.
Утверждение: функция суммы является многочленом k + 1-й степени относительно переменной n. Это утверждение можно доказать по-разному, например, можно доказать методом математической индукции (для перехода нужно взять производную от текущего многочлена).
Обозначим Px значение искомой суммы при n = x. Вычислим значения Px для всех целых значений от 0 до k + 1 (это легко сделать одним циклом за O(klogk)). Если n < k + 2, то мы уже нашли ответ. В противном случае давайте воспользуемся интерполяционным многочленом Лагранжа для получения искомого многочлена относительно переменной n.
Формула интерполяционного многочлена Лагранжа имеет вид: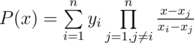 
. В нашем случае xi = i - 1, а yi = Pxi.
На этом разбор задачи был бы окончен, но это решение работает за квадратичное время от k, поскольку многочлен Лагранжа вычисляется за квадратичное время. Заметим, что у нас все узлы при интерполяции находятся на одинаковом расстоянии друг от друга (на расстоянии 1). Воспользуемся этим: заметим, что произведение внутри суммы для i + 1 может быть получено из произведения для i (нужно домножить текущее произведение на два числа и поделить на два числа). Таким образом, искомая сумма может быть посчитана за линейное время от k.
Сложность: O(klog MOD), логарифм повляется в связи с необходимостью поиска обратного элемента в поле по модулю MOD = 109 + 7.
very interesting round .. thanks a lot .. waiting for problem E
Done. F is left.
Thanks! I've learned a lot!
Задача является значительно упрощённой версией задачи предложенной Mohammad Nematollahi Deemo.
Если это упрощено, то какое сложное?
Не буду пока говорить. Может мы её всё-таки дадим на учебный раунд в полном виде)
Could someone help me with further optimization of my code for prob-c: not equal on segment It is giving tle on test-case 20.
`#include<bits/stdc++.h>
using namespace std;
int main() {
long long int n, m, l, r, x;
long long int a[n], first_on_left[n];
} `
Replace endl with "\n".
use scanf instead of cin. I got tle with cin several times.
The answer to the Infinite Sequence may be done in O(1). We may organize the sequence as: 1 (1) // That means the positions that the first one in that line is 1,2 (2) 1,2,3 (4) 1,2,3,4 (7) 1,2,3,4,5 (11) Then we would have a new sequence, which is much easier to find. 1 (1) 2 (2) 4 (3) 7 (4) 11 The number in the parenthesis are the distance between the number of the new sequence.
To find the base of the number we need to solve the equation x = n(n+1)/2 + 1. Where x is the number we receive as input. We need to isolate n (get the max floor value).
Then we use the n we got in the same formula, but now the result is going to be the base for the line. We only need to calculate the distance between the number we receive as input and the number we got as base.
x — base + 1
SOLUTION: 15944155
Actually A can be done in O(1).
We wanted to make the problem simple, so we gave it with the constraints for
solution.
as it turns out, A can be done in O(n) if you dare. My O(n) solution in C# + LINQ : 15953718
plz tell me how ?
Let's analyse how long it takes for the sequence to enter a new cycle:
C1=1 : 1
C2=1 2 : (from until here)1+2=3
C3=1 2 3 : (from until here)3+3=1+2+3=6
Ci=1 2 ... i : SUM from 1 to i = (i+1)(i)/2
So if we solve the equation (i+1)*(i)/2=n and get the floor of the positive root we can find in which cycle Ci the answer will come from.
Now you need to know how many numbers were used in the cycle.
(i+1)*(i)/2 is the quantity of numbers used to get past the cycle Ci.
If that result is equal to n, we know that the last number of the sequence is the answer so we print i. Else, i is the cycle right before the one the answer will come from, so we print n-(i+1)(i)/2 (the quantity of numbers used since the end of the last sequence)
Why my code for porb D 15942394 TLE?
I hope for some explanations from more experienced guys, but this code doesn't get TLE in Delphi 7. 15952130
Delphi 7 = FPC ??
Of course, not. They are two different compillers for two different languages. And your code works in D7 ~10 times faster, than in FPC.
thank
I don't know why, but it seems that the output buffer is not fast enough in fpc.
I made a little change: instead of using write() directly，save the things you want to output into a string, and finally writeln(the_string); and this way it passed all the test cases.
16055326
Кто поможет объяснить момент про задачу 622C на C#? Я использовал авторское решение, но получил на 20-м тесте TLE. Там где-то чуть больше секунды получается... Один раз даже прошел тест 20 за 1000 мс, но сразу же провалился на 21-м. Посмотрел, кто-то использовал
StringBuilder, попробовал у себя и оно прошло за 342 мс здесь. Почему такая разница?В задачах, в которых требуется много данных выводить как ответ, лучше использовать буферизированный вывод.
Спасибо! Попробовал исправить не прошедший до этого вариант без
StringBuilder, где я использовал массив строк с ответамиans[], но там я совершал ту же ошибку — выводил ответ с помощью цикла иConsole.WriteLine(ans[i]);, заменил цикл на одну строкуConsole.WriteLine(String.Join("\n",ans));и успешно прошел тесты за 358 мс. Возможно, кому-то это поможет.Actually we need O(k ln k) here due to calculating k-th power of each number.
Of course you are right. Fixed.
We can also do it in $$$O(k)$$$. Using linear-time sieve we can express each $$$i \leq k+1$$$ as $$$i = p \cdot j$$$ where $$$j<i$$$ and $$$p$$$ is prime. Then $$$i^k = p^k \cdot j^k$$$, so we only need to calculate the $$$k$$$-th powers for prime numbers up to $$$k+1$$$ and there are only $$$O(\frac{k}{\log k})$$$ of them.
As Far As I Know This Sequence "1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5...." Is Called "Doubly Fractal Sequence"
I Appl!ed Direct Formula :) ..
My Solution Was : http://ideone.com/NgIE6c
Справедливости ради, в F асимптотика все же
, а не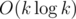 
.
Спасибо. Поправил.
Справедливости ради стоит заметить, что задача всё еще имеет решение за O(k log k), несмотря на то, что оно в разборе не написано :-) . Нужно всего лишь уметь считать обратные по модулю к факториалам за O(k)
Можно вроде как:
найдем n! = 1 * 2 * 3 * ... * (n-1) * n
найдем обратный к нему, запишем как:
1 / (1 * 2 * 3 * ... * (n-1) * n)
Чтобы получить обратный к (n-1)! надо вроде как всего лишь домножить на n и так далее.
UPD: понял, что написал достаточно очевидную вещь, видимо про быстрое нахождение обратных было скорей утверждение, чем вопрос :)
Спасибо. Я вот за 5 минут не придумал, как это сделать.
During contest in problem C, I used segment trees to solve. Got Time Limit Exceeded on 19th test case. Only problem was cin,cout. I should have used scanf and printf.
Those interested in segment tree solution of problem C :- http://codeforces.net/contest/622/submission/15960458
Did anyone solve D without writing brute force first? if yes then how did you think until you arrived to the solution?
allllekssssa sent me that problem and I solved it without brute force)
The only hard part in this problem is to predict that zero sum is achievable. After that it's nearly trivial to invent needed permutation.
I agree with you.
And I agree with both :)
I did that.
wrote a brute force first (for a given n, gives out all the possible permuations which have smallest sum).As it turns out:
the minimun sum is always 0.
too many possible sequences.
since it's a constructive problem, we want to find a simple sequence following some patterns.
Let's make some assumptions on possible sequence: there's always a required sequence, which 1 is the first one, and n is always the last one,（you can add more assumptions， since there are too many legal ones） which will lead to a very limited number of sequences. And a beautiful 1 3 5 7 ... 5 3 1 ... n may catch your eye, and now you can build one.
Why does this gives TLE? I think the complexity is O(n) which should satisfy the limits.
Don't mix cin/cout and scanf/printf. It's almost always bad idea. In that exact problem one definitely need to use scanf/printf due to big input.
15964463 (only difference is queries input)
Thanks a lot. Can you explain a bit more why was it giving TLE just because of input functions?
Maximal input size in the problem C is equal to
2*10^5 * 4 * 6 = 4.8 * 10^6characters, because there are2*10^5 * 4numbers and each one can be represented by 6 digits. Reading is a pretty slow operation, requiring approximately O(10) for each digit of a number, and it's particularly slow with built-in cin/cout streams. Cin/cout use various adjustments to make them more useful, e.g. there is a synchronization with scanf/printf which can sometimes come in handy, but it makes them extremely slow too. You'd want to turn it off, as it makes cin/cout much faster. Check out my codes, if you needAnyone solved C with plain binary search?
I wrote segment tree+binary search.
Pure binary search: 15971282
binary search , which has a binary search inside (Complexity: O(mlog2n))
My solution (in C# ):15936162
E is a very good problem :) I liked thinking the editorial solution.
В формуле многочлена Лагранжа должна быть k+1 вместо n в сумме и произведениях.
Эта формула в общем виде, для произвольных n узлов.
А ограничения в C специально так подобраны, чтобы не заходил ll и cin/cout?)
Конечно нет. Это типичные ограничения, чтобы квадрат не проходил.
Can anyone explain solution to problem F? I cant get the editorial.
P622C — Doing in O(n) but still getting TLE.
import java.util.Scanner;
Ok same code and I just changed cin cout with printf and scanf and now it's accepted. Can anybody explain this ?
http://codeforces.net/contest/622/submission/16016197
cout << endl flushes the output, use cout << "\n" instead.
Default setting of cin/cout is dramatically slow with such a huge input and output file.
Typically, there are three ways to fix it.
use scanf/printf instead
add std::ios::sync_with_stdio(false); at the very beginning of your main()
write fast I/O methods by your own.
Could anyone tell me more about problem F? I can't understand how we use Lagrange polynomial to solve that problem. Thanks in advance!
How can I optimize this O(n) Haskell solution to C so that it doesn't TLE? Or is it just a limitation of the language?
("build" preprocesses the values of p as described in the editorial. "solve" simply answers the queries using the array we built earlier.)
Can problem E be solved by dp on trees?
Problem C has a very elegant solution posted in the editorial, but just for the sake of learning, can someone tell me how to do it with square root decomposition ?