A. Подстрока
Думаю все поймут по коду:
p.s. При больших длинах можно воспользоваться алгоритмом КМП.
B. Третья степень
Ответ равен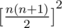 
по модулю P.
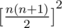по модулю P.Единственная проблема - при вычислении 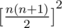происходит переполнение.
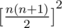происходит переполнение.Как избежать переполнения:
- Написать длинку
- Написать быстрое умножение по модулю (аналог быстрого возведения в степень)
Объясняю второй способ:
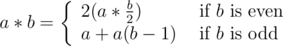
Псевдокод:
Очевидно что работает это за логарифм от b, так как у нас b делится на два каждый раз когда он чётный, а если он не чётный то мы отнимаем от него 1, и он на следующем шагу становится чётным.
C. Функция
Не знал, что проходит наивные решения с предпочётом и закидыванием в сэт или мап.
Ожидались решения с проверкой за О(1) битовыми операциями...
Этот способ должен работать даже если нужно было вычислить f(108)...
И так разбор...
Нужно было сделать то, что написано в условии - пройтись фориком, но быстро проверять.
Как быстро проверять:
Представим себе число X.
Для него существуют такие целые неотрицательные p и q, что 2p - 2q = X если представление X в двоичной записи эквивалентно:
63.........p................q.........0 - позиции
00000001111111100000 - число
Заметим, что (2p - 1) - (2q - 1) = 2p - 2q
Теперь рассмотрим 2p - 1:
63.........p...........................0
00000001111111111111.
Рассмотрим 2q - 1:
63...........................q...........0
000000000000000111111
И если отнять 2q - 1 от 2p - 1, то получится то, что нам нужно:
63.........p................q.........0
00000001111111100000
Теперь как проверить число на то, что она в двоичной записи такая 00000001111111100000:
1. Все правые нули сделаем единичками: X|(X - 1). Получится 00000001111111111111
2. Прибавим к 00000001111111111111 единичку. Получится 00000010000000000000
3. И проверяем, что число является степенью двойки(в ней только одна однёрка): X&(X - 1) = = 0
D. Непростая задачка
Есть несколько способов решить эту задачу. Вот мне известные:
1. Сжатым бором
2. Хэшами (наверняка это самый лёгкий способ)
3. Вроде и суффиксными деревьями тоже решается
4. Говорят прошёл и простой, не сжатый бор...
Решение хэшами:
1. Нужно перебрать все подстроки.
2. Вычислив их хэши запихнуть в массив.
3. Отсортировать хэши
4. Посчитать количество различных элементов.
Я не буду тут говорить, что такое хэши, а дам лишь ссылку (http://e-maxx.ru/algo/string_hashes) - там всё подробно описано.
E. Подматрица
Так получилось, что и эта задача решается хэшами.
Идея подчёта хэша подматрицы - считать хэш хэшов (способ 1):
h1 = hash(A1, 1A1, 2 ... A1, b)
h2 = hash(A2, 1A2, 2 ... A2, b)
...
ha = hash(Aa, 1Aa, 2 ... Aa, b)
hash(A) = hash(h1 h2... ha)
Асимптотика O(a * b + c * d).
Идея подчёта хэша подматрицы (способ 2):
От KhaustovPavel:
В задаче E можно обойтись обычным хэшиком по одному прайму. Если мысленно склеить все строки подматрицы в одну строку, то найти хеш такой строки не составит проблем. Если предпосчитать хеши с каждой позиции на b элементов влево (где это допустимо) и предпосчитать все степени прайма до C * D, то дальнейшее решение можно реализовать за O(C * D) и использовать лишь один прайм.
B: сразу юзал oeis и вспомнил недвание топики на кф про умножение long long.
C: для меня сразу было очевидно решать влоб, проверяя калдовством с битами. Сразу пришла в голову мысль сбросить последние нули простым (while(!(a&1)) a>>=1), а потом проверка (a&(a+1)==0). Долго думать не стал, это и закодил. Правда тут косяк..while работал бесконечно - нужно было проверить a на равенство 0.
D: понятно хэши, понятно с e-maxx :)
E: тут поинтереснее. Вначале начал кодить хэши по строчкам и по столбцам и потом объединять. Когда в конец запутался пришла другая мысль. Считаем хэши для прямоугольников от (0;0) до (i,j), по формуле (h[i][j] = (s[i][j] - 'a' + 1) * p_pow[i*c+j]+h[i][j-1]+h[i-1][j]-h[i-1][j-1];) Тут как и в хэшах со строчкой каждому элементу матрицы свой множитель (p^( i*c+j )). А теперь совсем просто:
если hh*p_pow[(i-a+1)*c+(j-b+1)]==aa, где hh - хэш данной подматрицы ( hh+= (s1[i][j] - 'a' + 1) * p_pow[i*c+j]; ), aa - хэш рассматриваемой подматрицы заканчивающийся позицией (i,j).
p_pow[(i-a+1)*c+(j-b+1)] - это та разница, как и в хэшах по строке, которая компенсирует сдвиг.