Итак, совсем недавно завершился первый раунд Snark News Summer Series. Предлагаю тут его обсуждать, а также напишу небольшой разбор.
Задача А
Вероятно, самая простая задача раунда, с которой и начали большинство участников. Для ее решения следовало заметить, что существует ровно 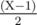 свободных бит в палиндромах с длиной битовой записи Х - биты, начиная с второго по сташинству, до середины строки. То есть палиндромов с длиной битовой записи Х всего
свободных бит в палиндромах с длиной битовой записи Х - биты, начиная с второго по сташинству, до середины строки. То есть палиндромов с длиной битовой записи Х всего 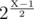 . Таким образом можно узнать длину битовой записи палиндрома, который нам нужен, и номер нашего палиндрома среди всех палиндромов такой длины. Ну а само число тогда получить уже очень просто:
. Таким образом можно узнать длину битовой записи палиндрома, который нам нужен, и номер нашего палиндрома среди всех палиндромов такой длины. Ну а само число тогда получить уже очень просто:
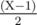 свободных бит в палиндромах с длиной битовой записи Х - биты, начиная с второго по сташинству, до середины строки. То есть палиндромов с длиной битовой записи Х всего
свободных бит в палиндромах с длиной битовой записи Х - биты, начиная с второго по сташинству, до середины строки. То есть палиндромов с длиной битовой записи Х всего 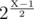 . Таким образом можно узнать длину битовой записи палиндрома, который нам нужен, и номер нашего палиндрома среди всех палиндромов такой длины. Ну а само число тогда получить уже очень просто:
. Таким образом можно узнать длину битовой записи палиндрома, который нам нужен, и номер нашего палиндрома среди всех палиндромов такой длины. Ну а само число тогда получить уже очень просто:1). Пусть S - первая половина искомого палиндрома. Тогда ее старший бит - 1, а следующие биты - это двоичная запись номера нашего палиндрома, дополненная сначала нулями так, чтобы длина S была равна X / 2 + X%2.
2). Ответ - это S + S', если длина палиндрома четная, S' - перевернутая строка S. Если длина нечетная, то у S' надо просто откусить первый символ.
Интерестно, есть ли решение формулой.
Задача Б
Пожалуй, эта задача мне понравилась больше всего. Как раз то, что надо как одна из 6ти на 80 минут - немного покодить, немного подумать, есть, где допустить баг.
Для начала надо было запомнить все сгибы листка, которые происходили в действительности (то есть линия сгиба проходила не за листком) и записать координаты 4 углов после каждого такого сгиба.
Затем надо было пройти с конца по этому массиву, храня на каждом шагу множество дырок в листке, и переходя к множеству дырок на развороте листка.
Как мне кажется, падали участники на том, что не проверяли, что после разворота точки находятся по-прежнему на поверхности листка. Недостаточно также было возвращать те точки, которые после всех разворотов находятся на изначальном листке - в процессе разворачивания могли возникнуть фиктивные точки, которые потом попали на изначальный листок.
Задача С
Я эту задачу, как и многие другие, решал паросочетанием. Можно заметить, что четность суммы координат клетки, где стоит конь, и тех полей, куда он бьет, различна. Таким образом можно разбить все поле на два типа клеток, и проверсти ребра между теми парами невырезанных клеток, в которые находятся на расстоянии хода коня друг от друга. После этого в полученном графе построить максимальное паросочетание и поставить коней на паросочтенные клетки одной из доль (то есть только с четной суммой координат, к примеру). Могло показаться, что паросочетание не пройдет, но это заблуждение:) Тут 5000 вершин, из каждой по 8 ребер. В Харькове за 3 секунды почти все участники пропихнули паросочетание на 50000 вершин, из каждой из которых было 32 ребра (2011 год, 9 день, "Регулярное паросочетание").
И еще мне кажется, что тут проходила какая-то жадность. Идеи?
Задача Д
Не люблю такие задачи. 25с, 666 тестов. Непонятно, должно ли решение выполнять макстест на 25/666 с., или в файле не будет много макстестов, и пройдет какой-то пропих. Я пытался сдать в дорешивании динамику по подмаскам и перебор, оптимизированный запоминанием. Перефразируя Томаса Эдисона, я не зафейлил - я написал 26 кодов, которые делают что-то другое:)
ПС. Хотелось бы услышать, как сдавали те, кто сдали.
Задача Е
Неплохая задачка, но, по-моему, ограничения чуть-чуть переподкручены. Решение - две динамики:
F[V, M] - максимальный поток, могущий идти вверх из вершины V если мы на ее поддерево потратили M миллионов. (Пропускная способность ребра над этой вершиной не учитывается.)
G[V, M] - максимальный поток, могущий идти по ребру от вершины V вверх, если мы на ее поддерево и на ребро вверх от нее в сумме потратили M миллионов.
Ну и переход изящен и самоочевиден:
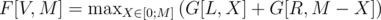
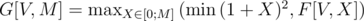
ПС: Если не самоочевиден - деньги вершины надо разделить между левым и правым поддеревом и ребром в поддерево. Деньги вершины и ребра в нее надо разделить на деньги в вершину и деньги, потраченные на ребро.
L, R - правый и левый потомок вершины. Для листьев F[Leaf, M] = C[Leaf] + M, где C[Leaf]- количество изначально вырабатываемой в листе нефти.
Что раздражает - другое, более сложное решение, с такой же ассимптотикой O(N * M2) не прошло по ТЛу, такое же решение, только не двумя циклами, а двумя функциями, которые друг друга вызывают - тоже. Это зашло меньше чем за 3с. при ТЛе в 4.
Задача Ф
Ну, построить двудольный граф по правилу "если в инпуте есть ребро i → j, то провести ребро из вершины i левой доли в вершину j правой", построить максимальное паросочетание и вывести его, если оно совершенное. Хм. Где-то выше я это уже писал. По-моему. И по-моему давать в одном контесте две задачи, которые решаются одним и тем же алгоритмом (хотя, может, могут быть решены и по-другому) - незачет.
Еще сильно расстроил плохой тест по задаче Е - я-то с ним только в дорешивании боролся, а вот участники врея потеряли.










