Задача А
Как решал я. Для каждого слова посчитал хэш, запихал все в сет. Потом для каждого префикса каждого слова считал его хэш, и хэш оставшейся части (амортизационно - за О(1) ), и проверял, есть ли хэши обеих частей в сете. Почему-то упорно получал ВА(5). Кто сдавал так же - в чем может быть проблема, и заходило ли такое решение?
Задача B
Не писал, но вроде бы все что надо - аккуратно построить граф с вершинами-участками и ребрами-стримостями сноса стен между ними, и затем в нем найти минимальное остовное дерево. Вопрос - что делать с внешней территорией. Можно рассмотреть 2 случая: когда она не входит в оптимальное решение (просто строим остовное дерево в исходном графе) и когда входит (по сути, получаем еще одну вершину в исходном графе).
Задача С
Буду благодарен за разбор
UPD: разбор от Jokser'а см. ниже в комментариях
Задача D
Противная задача с нечеткими ограничениями, но все, что нужно - как-то написать то, что описано в условии. Для быстрой проверки того, выбрал ли пользователь i приложение j я завел битовую матрицу 10000 x 10000, проверку для каждого пользователя делал фактически в лоб (даже без всяких бинпоисков), логично предполагая, что хитрых тестов с такими раздолбайскими ограничениями не будет. Задача зашла мгновенно.
Задача E
Почему-то относительно мало участников сдавали, хотя задача, имхо, проще той же D. Выполняем бинпоиск по ответу, для каждой длины в лоб за O(N2) проверяем, подходит ли эта длина. При заданных ограничениях без всяких оптимизаций просто летает.
UPD: как указал jte ниже, задачу можно решать даже целочисленно (если умножить все длины на 2 и потом не забыть разделить ответ на 2), что еще более ускоряет поиск ответа.
Задача F
Посидев несколько минут с карандашиком, можно было вывести нехитрую формулу 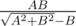 при A <= B;
при A <= B;
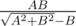 при A <= B;
при A <= B;










один в один), которое Вы описали выше.Будем последовательно рассматривать все N вертикальных рядов. Для текущего ряда будем перебирать все интернет-кафе и для каждого кафе найдем точки пересечения с данным вертикальным рядом - некий отрезок [L;R]. Я это делал 2-мя бинпоисками: фиксировал некую центральную точку X - точка пересечения горизонтального отрезка, проведенного из центра кафе с вертикальным рядом. А дальше одним бинпоиском увеличивал верхнюю границу, вторым нижнюю. Запихиваем отрезки в массив и сортируем по левой границе, также дублируем и сортируем по правой. А дальше в лоб перебираем текущую точку Y на вертикальном отрезке. Заводим 2 указателя, первый проверяет левые границы и включает отрезок в текущие, которые покрывают Y, второй проверяет правые границы и отрезки исключает. Тогда для каждого Y можно несложно найти ответ. Итого сложность получается O(N*K*logM + N*M)
Код: http://pastebin.com/K9dMLZBF
Можно же вместо бинпоисков воспользоваться теоремой Пифагора :)
Да и от M во времени работы алгоритма можно избавиться.
Например, добавляем Li - начало отрезка с пометкой о том, что это начало, и Ri + 1 - следующую за концом отрезка точку с пометкой о том, что это конец.
Сортируем, бежим по отсортированному массиву. Если встретили начало - увеличиваем сумму, если конец - уменьшаем. Если расстояние до следующей точки в отсортированном массиве больше нуля, естественным образом обновляем ответ.
И самое главное - перебирать номера столбцов от 1 до N, а не от 0 до N - 1. :)