Специально по просьбе JKeeJ1e30.

Задачи второго дивизиона и A с B первого уже разбирались ранее, поэтому я опишу только решения C и D.

C. Петя и Пауки
Поначалу могло показаться, что это задача на конструктив, но такую мысль нужно сразу откидывать. Конструктивные решения ломались тестами 4 4, 7 4 и 5 6.
Если заметить, что nm ≤ 40, и понять, что доску можно вращать, то из простого рассуждения, что меньшая сторона доски не больше 6, становится ясно, что задача - на какую-то динамику по профилю.
Моё решение - такое. Будем считать не максимальное количество оставшихся клеток, а минимальное количество центров, в которые могут сбежаться все пауки. Повернём доску, чтобы количество строк было не больше шести.
Пусть D[k][pmsk][msk] - это минимальное количество центров, достаточное, чтобы собрать всех тараканов с первых k столбцов, причём k-ый столбец имеет маску pmsk, а k+1-ый - msk. Тогда за переход мы перебираем маску tmsk k-1-ого столбца, и среди тех, для которых k-ый столбец может целиком разбежаться по центрам, выбираем тот, для которого D[k - 1][tmsk][pmsk] минимально.
Получается решение за O(n * 2^3m), где n > m.
Другие варианты решения, которые я видел:
Можно как-то схлопнуть две двоичных маски в одну троичную, честно говоря, я не вникал, как именно.
Можно насчитать ответ для всех входных данных, благо тех совсем немного, каким-нибудь оптимизированным перебором. Например, перебирая маски центров в порядке возрастания количества бит.
D. Петя и раскраски.
Тут нужно посидеть, подумать, и вывести пару формул.
Во-первых, когда m = 1, ответ - kⁿ, потому как подходит любая раскраска.

Когда m > 1, обратим наши взоры на два крайних столбца. Проведём прямую справа от левого крайнего столбца. Слева и справа от неё должно быть одинаковое количество цветов - пусть X. Теперь заметим, что если начать двигать эту прямую направо, количестов различных цветов слева будет неуменьшаться, а справа - неувеличиваться. А раз эти два количества должны оставаться одинаковыми, то ни одного увеличения/уменьшения происходить не должно. Значит все возможные цвета, которые могут оказаться слева от прямой должны присутствовать в крайнем левом столбце, а все возможные цвета, который могут оказаться справа от прямой - в крайнем правом столбце.

Иными словами, множество цветов на всей доске должно иметь вид 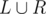, где |L| = |R|, а множество цветов в левом и правом столбце - L и R соответственно. При этом заметим, что в оставшихся столбцах могут присутствовать только цвета из - иначе нам поломает всё условие.

Что же, это даёт следующий алгоритм.

Зафиксируем 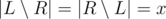и 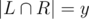(должны выполняться условия 2x + y ≤ k и x + y ≤ n. Тогда во-первых, ответ нужно домножить на 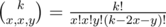- это количество способов выбрать соответственно x, y и x цветов в множества .

Далее, все клетки между крайними столбцами можно покрасить в произвольный из y цветов, значит ответ домножается на k^n(m - 2).

Потом, нам надо покрасить крайние столбцы. Количество способов покрасить столбец в x цветов так, чтобы все цвета присутствовали, считается динамикой D[x] следующим образом: 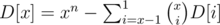. Наконец, ответ домножается на вышепосчитанное D[x]².

С реализацией этого решения может быть некоторое количество проблем. Я лично столкнулся с тем, что оно адски тормозило. Оказалось фатальным делать O(k) взятий обратного элемента за логарифм в лонг лонгах. Помогли следующие оптимизации - предподсчитываем все биномиальные коэффициенты до 2000, расписываем 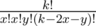как 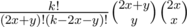- последние два выражения у нас предподсчитаны. Можно было бы также просто предподсчитать обратные факториалы - у нас будет использоваться O(n) значений обратных факториалов.

Конкретно реализацию можно посмотреть в моём, например, коде.

Присоединяюсь к общему вопросу: авторы, где разбор? А конкретно его часть, относящаяся к задаче E? :-)