Можно разобрать четыре случая, а можно заметить, что если обозначить front/back за 0/1 (b), а из a вычесть единицу, то a XOR b будет ответом (0/1). Время и пямять - O(1).

Решается "в лоб" одним циклом: пока k-й вопрос сыгран, увеличить k на один, и, если k > n, то k = 1. Время и пямять - O(n).

Одним из решений было написать ровно то, что просят в условии. Итераций Винни-Пуха будет не более 3n (к каждой банке он обращается не более 3-х раз), каждую итерацию можно выполнить за O(n) (поиск максимума в массиве). Время - O(n²) ≈ 10⁴ операций, память - O(n).

Но есть решение короче: давайте заметим, что порядок поедания мёда ни на что не влияет. Теперь посмотрим на то, сколько мёда из каждой банки съест Винни-Пух, а сколько оставит Пятачку. Нетрудно понять, что если a_i >  = 3k, то Винни-Пух оставит Пятачку a_i - 3k килограмм, а если a_i < 3k, то 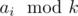. Теперь решение задачи - один цикл. Время и память - O(n).

Сначала переберём, какими будут разделяющие прямые - горизонтальными или вертикальными. Чтобы не повторять два раза кусок кода, можно просто повернуть поле на 90 градусов и повторить поиск какого-нибудь одного типа (например, вертикального). Перебираем границы раздела (так, чтобы все области были непустые), считаем суммарное количество кукурузы в каждой области и сравниваем с тем, что надо получить (например, можно отсортировать и сравнивать поэлементно). Если совпало - увеличиваем ответ на 1. Общее время работы - O(n²· m²) ≈ 6.25·10⁶ операций, память - O(nm)

Утверждается, что ответ - 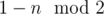. При чётных n выигрывает второй игрок (Гена), при нечётных - первый (Петя). В первом случае второй игрок ставит коня симметрично первому игроку (относительно центра поля). Во втором случае первым ходой Петя ставит коня в центр доски, а далее ставит симметрично ходам Гены. Можно понять, что при данных стратегиях выигрывающему игроку не придётся ставить коня под бой. Таким образом имеем решение за O(1) времени и памяти.

Ответ - сумма длин всех паучков. Очевидно, как такой ответ достигается - склеим паучков в цепочку так, чтобы самый длинный путь в одном паучке кончался в начале самого длинного пути другого паучка.

Докажем, что лучше нельзя: в самом деле, пусть мы как-то склеили паучков и получили ответ лучше. Посмотрим на самый длинный путь. Он сначала проходит по одному паучку, потом по другому и т.д., причём паучки не повторяются, иначе путь имеет самопересечения. Значит, длина пути не больше, чем сумма длин максимальных путей в каждом паучке, что и требовалось доказать.

Длину паучка можно искать перебором начальной вершины пути и запуском DFS'а. Время работы - 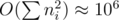операций, кол-во используемой памяти зависит от того, как вы работете с графом. В любом случае, 256 МБ должно хватать.

Опять задача, в которой требовалось написать то, что написано в условии. Заводим все необходимые массивы и очередь карт, которые еще в игре. Теперь просто эмулируем. Код.

Заметим, что всевозможных строк длиной до 4-х символов всего лишь 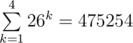. Это небольшое число. Давайте занумеруем всё такие строки следующим образом: обозначим отсутствующий символ за 0, а символы a..b - 1..26 и посчитаем полиномальный хэш: id(a₀ a₁ a₂ a₃) = a₀· 27³ + a₁· 27² + a₂· 27 + a₃. Заметим, что для всех строчек он будет различен и принимать значения в отрезке [0; 27⁴ - 1 = 531440].

Теперь заметим, что каждую из строк можно заменить максимум на 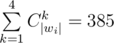, где (|w_i| - длина i-го слова) коротких слов. Давайте построим двудольный граф. В одной доле будет n вершин, соответствующие словам, а в другой доле - все короткие слова. Ребро из a в b проводится в том, и только том случае, если a можно заменить на b. Теперь наша задача свелась к нахождению в этом графе максимального паросочетания и проверке, что в него входят все вершины слева. Это можно сделать алгоритмом Куна. Время работы - O(n₁· m), где n₁ - количество вершин первой доли, а m - количество рёбер графа. O(n₁· m) ≈ 200· 200· 385 = 15.4·10⁶ операций, что прекрасно укладывается. Для сохранения времени работы необходимо хранить граф в виде списков смежности. Т.о. используемая память - O(n₁ + m), что также немного.

К сожалению, моё решение этой задачи довольно громоздко. Если кто-нибудь поделится более изящным вариантом - буду рад.

Идея решения довольно стандартная: фиксируем префикс числа и проверяем, можно ли получить ответ при таком префиксе (хоть как нибудь). Потом просто перебираем все цифры с начала числа, значения для них и делаем переход к следующей цифре, как только получили, что с текущим значением ответ реален. Если при этом префикс стал больше соответствующего префикса исходного числа, то говорим, что теперь мы можем ставить вообще любые цифры, а не только больше изначальных.

Теперь решение для подзадачи. Оно довольно просто - забъём хвост восьмёрками и посчитаем ответ. Очевидно, что лучше нельзя.

Решение выше хорошо всем, кроме времени работы. Если каждый раз честно пересчитывать максимальный ответ для "хвоста", то время работы будет порядка O(n²). Чтобы измежать этого, можно заметить, что при изменении номера фиксированной цифры на единицу, ответ для хвоста пересчитывается по довольно простым законам, правда, разным для первой и второй половин.

Если добавить пересчёт, решение станет работать за O(n) и требовать O(n) памяти, чего хватает.

Первое замечание - ответ можно искать только среди векторов с неотрицательными координатами. Т.е. можно с самого начала преобразовать все вектора с хотя бы одной отрицательной координатой, забыть про преобразования и ответ не ухудшится. Это несложно проверить, посмотрев, как мог измениться ответ.

Теперь задача такова: есть n точек на плоскости, надо найти две ближайшие. Это стандартная задача на метод разделяй-и-властвуй. Этот алгоритм описан на e-maxx.