Несмотря на то, что участники уже опубликовали собственный разбор, предлагаем вам авторский разбор контеста.
Задача A. Лифт.
Автор --- Кудряшов Игорь.
Данная задача является утешительной задачей контеста. В ней нужно рассмотреть 4 случая. Если пассажир зашел через переднюю дверь и держался за 1ый поручень, или он зашел через заднюю дверь и держался за 2ой поручень, то нужно выдать сообщение о том, что он левша. Если же пассажир зашел через переднюю дверь и держался за 2ой поручень, или он зашел через заднюю дверь и держался за 1ый поручень, то пассажир является правшой.
Задача B. Что? Где? Когда?
Автор --- Бондаренко Полина.
Условие задачи можно переформулировать следующим образом: найти первую справа 1 в зацикленном массиве, если в ячейке с номером k стоит 0.
От ячейки с номером k движемся направо по массиву, пока не встретим ячейку с 1 или не закончится массив. Если дошли до конца массива, а 1 еще не встретили, то начинаем идти с начала. Т.к. по условию гарантируется, что хотя бы одна единица существует, то за один проход мы найдем ячейку с единицей.
Задача C. Винни-Пух и мед.
Автор --- Матов Дмитрий.
В этой задаче требуется промоделировать процесс поедания меда Винни-Пухом. Чтобы это сделать, нужно хранить для каждой банки количество оставшегося в ней меда, а также количество раз, которое Винни уже ел из этой банки. Можно решить задачу и проще: заметим, что не имеет значения, в каком порядке Винни-Пух ест мед из банок. Поэтому все банки можно обрабатывать по-отдельности. Тогда отпадает необходимость в моделировании: для каждой банки сразу можно понять, сколько меда в ней останется. Пусть в банке изначальн X килограмм меда. Тогда, если X ≥ 3k, то Винни-Пух съест из этой банки 3k, а останется X - 3k. Если же X < 3k, то в банке останется 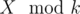 килограмм меда.
килограмм меда.
Задача D. Три сына.
Автор --- Николай Кузнецов.
По условию задачи требуется разделить поле на три части так, чтобы
суммарное количество кукурузы в первой, во второй и третьей частях
было равно A, B, C. Кроме того, следует обратить внимание, что
порядок, в котором достигается равенство, не важен.
Эта задача достаточно проста. Можно перебрать все способы разрезать
поле по вертикали, все способы разрезать по горизонтали и подсчитать
количество из них тех, которые разрезают поле на части A, B, C.
Очевидно, что разрезов суммарно O(n2 + m2). Суммарное количество
кукурузы можно подсчитать за время O(nm). Итого, наше решение имеет
время работы, пропорциональное 4-ой степени от n и m, но при данных
ограничениях это годится.
Задача E. Поставь коня!
Автор --- Агапов Геральд.
Заметим, что в этой игре выигрыш зависит от четности n. Если n четно, выигрывает второй игрок, если нечетно --- первый.
В случае четного n второй игрок может всегда ходить симметрично ходам первого относительно центра поля. Тогда понятно, что если ход у первого существовал, то и у второго также будет существовать ход. Значит выигрывает второй.
В случае нечетного n первый игрок может поставить первым ходом коня в центр поля, а дальше ходить симметрично ходам второго игрока.
Задача F. Пауки.
Автор --- Бондаренко Полина.
Рассмотрим решение задачи для одного паука.
Паук представляет собой граф - --дерево. Решением задачи для него будет длина максимального пути в дереве (или диаметр). Диаметр в дереве можно найти несколькими способами. Один из них --- посчитать от каждой вершины расстояние до каждой и выбрать максимум из этих величин, т.к. граф --- дерево. Асимптотика решения O(n2), где n --- количество вершин в дереве.
Решив задачу для каждого паука, складываем найденные диаметры --- это и будет ответ на задачу.
Задача H. Краткость --- сестра таланта.
Автор --- Холкин Павел.
В данной задаче нужно построить взамно однозначное соответствие одного множества на другое. В данном случае в качестве первого выступает множество исходных слов, а в качестве второго --- множество их сокращений. Обычно такие задачи решаются при помощи нахождения максимального паросочетания. Построим следующий двудольный граф: вершинам первой доли будут соответствовать исходные строки, а вершинам второй --- их сокращенные аналоги. Сокращенные аналоги для исходных строк сгенерируем следующим образом: для каждого слова i исходного множества переберем всевозможные подпоследовательности длины от единицы до четырех. Каждому полученному слову присвоим уникальный номер j, которое будет являться номером соответствующей вершины во второй доле. При этом, разумеется, если полученное слово уже являлось сокращенным аналогом какого-то другого слова из исходного набора, то просто возьмем уже присвоенный ему ранее номер. Теперь добавим ребро (i, j) в наш двудольный граф, которое будет означать, что i-ое слово из набора можно сократить каким-то j-ым сокращением, которое мы сгенерировали. В этом графе найдем максимальное паросочетание, например, алгоритмом Куна. Если в результате для каждой вершины первой доли нашлась пара, значит ответ существует и для каждого слова нужно вывести найденное его сокращение. В противном случае нужно вывести -1.
Задача I. Счастье в числах.
Автор --- Матов Дмитрий.
Обозначим левую половину билета за x = x1, x2... xn, правую за y = y1, y2... yn. Пусть счастливость заданного билета равна h. Попытаемся сначала найти искомый билет среди таких, у которых левая половина равна x.
Будем перебирать по убыванию l (от n - 1 до 0) --- длину префикса второй половины, которая будет совпадать у заданного билета и у искомого. Затем переберем цифру в позиции l + 1 искомого билета. Перебирать цифру будем в порядке возрастания, причем будем рассматривать только цифры, большие, чем yl + 1. Зафиксировав таким образом первые l + 1 цифру в правой половине искомого билета, будем жадно достраивать его лексикографически минимальным способом с учетом того, что его счастливость должна быть больше h. Более подробно: будем перебирать очередную цифру по возрастанию. Для того, чтобы проверить, можно ли ее поставить, нам нужно быстро посчитать максимальную счастливость, которую мы можем получить, расставляя цифры в конце. Для этого мы должны предположить, что заполним хвост восьмерками. Нужно научиться считать это за O(1).
Если не удалось жадно построить ответ описанным образом, то это значит, что нужно искать среди билетов, у которых левая часть отлична от x. Заметим, что билет, у которого левая часть совпадает с правой, т.е. билет вида zz имеет максимальную счастливость среди всех билетов с левой половиной z. Поэтому сначала найдем билет вида zz такой, что его номер больше xy, и счастливость больше h. Сделаем это жадно: переберем длину t совпадающего префикса у x и h в порядке убывания, попробуем поставить в позицию zt + 1 цифру большую, чем xt + 1, а затем будем пытаться дополнить z лексикографически минимальным способом с учетом того, чтобы суммарное число подсвеченных сегментов в z (т.е. счастливость билета zz) было больше h. Если нам это удалось, то правую часть билета можно также достроить жадно, используя аналогичные рассуждения.
Задача J. Минимальная сумма.
Автор --- Агапов Геральд.
Запишем сумму двух векторов v = (x1, y1) и u = (x2, y2) : s = v + u = (x1 + x2, y1 + y2).
Длина вектора s есть |s| = (x1 + x2)2 + (y1 + y2)2. Понятно, что как ни расставляй знаки у координат,
минимальным значение длины будет в случае, когда s = (|x1| - |x2|)2 + (|y1| - |y2|)2.
Таким образом наша задача равносильна следующей: перевести все векторы в первую четверть (сделать координаты неотрицательными), и далее найти два вектора, длина разности которых минимальна, что в свою очередь равносильно нахождению двух ближайших точек на плоскости. Существует вполне известный алгоритм, который с помощью метода "разделяй и властвуй" находит две ближайшие точки за O(n· log(n)).
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
35:05:06
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
35:05:06
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
Write comment?
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 06:29:55 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










