Мой первый пост — о контесте №10.
A. Учет энергопотребления
В этой задаче всего-навсего нужно было имитировать работу ноутбука. Будем записывать результат в переменную res. Для каждого интервала прибавим к res число (ri - li)· P1, т.к. во время интервалов ноутбук работает на полную мощность. Обозначим функцию
int foo (int &m, int t) {
if(m < t) t = m;
m -= t;
return t;
}
Далее для каждого i < n к res применим следующие действия: пусть время между концом i-ого и началом (i + 1)-ого интервалов — tmp. Тогда прибавим к res
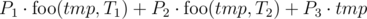. Переменная res и является ответом задачи.Думал, что программа запорется на крайних тестах. Оказалось, ошибочно думал — AC.
B. Кассир в кинотеатре
Сразу начал искать какой-нибудь быстрый алгоритм, на это потратил какое-то время. Потом подумал —"а зачем?" и написал bruteforce.
Алгоритм простой до безобразия и без оптимизаций (
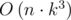). Идём по всем возможным позициям x, y, если все выбранные места не заняты, считаем данную в задаче функцию для выбранных чисел, минимум вместе с координатами фиксируем в переменную. AC с первого раза.C. Цифровой корень
Математика, обрадовался я. Известный факт, что
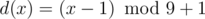. Заметим, что для задачи не важно, d(x) = 9 или d(x) = 0: в принципе это одно и то же. Поэтому можем упростить: 
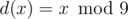.Посчитаем, сколько троек чисел удовлетворяют Васиному условию. В массиве A[9][9]
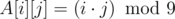: чтобы знать значение d(i· j). В массиве B[9] B[i] — количество чисел, не больших n, которые дают остаток i при делении на 9. Итак: для каждых i, j количество искомых троек таких, что d(i· j) = d(l), является B[i]· B[j]· B[A[i][j]] (все эти тройки удовлетворяют Васиному суперусловию). Складывая все эти числа, получаем искомое (X).Теперь посчитаем, сколько троек Вася найдёт правильно своим условием. Подумаем: ведь это те и только те тройки A, B, C, которым выполняется A· B = C ≤ n. То есть, произведение A и B не более n. Как найти это количество? Очевидно, что как A и B годятся все числа 1 и i, i ≤ n. Так же годятся все числа 2 и i,
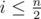. И так для каждого i как A годятся все числа B, которые не больше 
. Вся их сумма — искомое количество (Y).Ответ — X - Y. Ну, думаю, сейчас уж не прокатит третий раз с первого раза. И внезапно — AC. Ну тут я обрадовался.
Посмотрел на задачи D и E. Вижу, почти никто D не решил. Однако всё-таки посмотрел, подумал, что DP, подумал, что уже раньше что-то подобное видел. Но писать что-то уже было влом, да и наверное, беcперспективно, раз даже лидеры не решили. В E тоже особенно не вдумывался. Поняв, что за полчаса не решу ни одну из этих двух задач, на этом и закончил. Впечатления: хороший контест, особенно понравилась задача C.
Ну, к определённому успеху я пришёл — поднялся с Сержанта (1466) до Лейтенанта (1610): +144. Ну что, отлично.
Помню еще у Гарднера было что-то интересное про числовые корни (книга "Гарднер М. Матемачиские чудеса и тайны"), но доказательства вроде бы там нет.
В задаче 10D - НОВП проходит наглая динамика за O(n^2*m^2), хотя, как бы, по ограничениям не должна. Странно, что в системе нет теста, который валит это решение, хотя он и очевиден — 500 единиц в первом и во втором массивах.
Может, за три года компьютеры стали быстрее? =)
В задаче D большинство решений валится тестом 7 3 4 5 6 1 2 4 6 1 2 3 4 5 6 Здесь же имеет полное решение