EDIT: Solutions are available @ http://www.bitwise.iitkgp.ernet.in/solutions
Hi all, Bitwise is an algorithm intensive programming contest organised by the Department of Computer Science and Engineering of IIT Kharagpur. Prizes worth $4000 (INR 2 Lakhs) are on the cards. Allowed Programming Languages are C/C++/Java.
Bitwise is scheduled to be on 12th February 2012. The Contest will start at 1030 hrs and end at 2230 hrs (UTC)
Register here: http://www.bitwise.iitkgp.ernet.in/register Main Website: http://www.bitwise.iitkgp.ernet.in/home
The break up of the prizes are as follows:-
Global Top 3:- 1st Place: 60,000 INR (~**1200** USD) 2nd Place: 35,000 INR (~ 700 USD) 3rd Place: 25,000 INR (~ 500 USD)
Indian Top 3:- 1st Place: 10,000 INR 2nd Place: 6,000 INR 3rd Place: 4,000 INR
There are other prizes for the global Top 20 as well — http://www.bitwise.iitkgp.ernet.in/home#prizes. So don't forget to participate!











Неправильная локаль
For the God sake, it is 2012. Still no Java?
Our team is working to support Java as well; Will definitely let you know in a couple of days!
Java solutions will be accepted!
Thank you for this Also I hope this year all limits on input data would be available from the start
Yes, we will ensure that.
Even if they include java, there is very bleak(small) chance for any java coder wining, because the scores are evaluated on the basis of correctness, TIME and SPACE efficiency.
Actually there is standard tl and ml, at least that was the case for some last years
As Egor correctly pointed out, there is a standard time and memory limit. Your solution just has to be within those limits — then you would be given full credit!
Now it is clear. When I read the FAQ's on website I misunderstood the context of time and memory limit.
During Bitwise 2011, there was a problem which allowed precalculation of answers to all possible test cases on a local computer and then sending a simple program that just prints the right answers. Doing so is pretty legal in a number of other contests. However, in the middle of the contest, a rule appeared which informally rejected such submissions. From a participant's point of view, it was a bit inconvenient to see the rules change in the middle of the contest.
If you plan to include a problem which allows precalculation in Bitwise 2012, please either accept such solutions entirely or make a clear and formal rule against them and publish it in the competition rules and/or the problem statement.
To disallow such solutions in a formal way, there is often a limit on the source code size (e. g., 50 000 bytes on CodeChef or Sphere Online Judge, 256 KB on some ACM ICPC contests).
@Gassa: Yes, I am aware of the fact (on the receiving end as a participant). Rest assured, it won't happen this time. Thanks for the suggestion about the source limit. We will specify beforehand in the problem statement/Rules about any such limits.
Do I understand correctly that C++ programs will be compiled without -O2 flag?
Yes, only the -lm flag is specified
Can you clarify about prizes, like if someone is in both list, global and india, then will they be counted in both list ?
Well, no. But they will get the better of the two. So if an Indian comes in Global Top 3, then he gets the global prize.
so, the 11th place in India will slide-up, right ?
like if "x" comes in global top-3. then also the indian list will have 10 names excluding his name.
I cannot submit as of now, rights?
Java compiler considers warnings as errors, can you fix this?
We are working on this...it requires some changes in our system because of -Xlint warnings. Please try removing the warnings for now.
Ну как, как, блин, эта третья решается?
я вот так и не понял вв чем там подвох. тоже не сдалась. я решал деревом отрезков, тестил долго....
Ну, если тупо деревом отрезков, то там слишком большие числа получаются в длинке и это проходит 1 тест — на втором тл
так там же по модулю.
Ну а как зная модули двух чисел найти их НОК?
nok(a,b) = (a*b) * inv( gcd(a,b) ). а обратный элемент по модулю простого числа через возведение в степень.
а как найти gcd двух чисел, если мы их знаем только по модулю?
даблпост (100 лет ведь уже не было, да?)
да, я ступил) забыл, про остаток от деления в gcd. видимо, лучше было хранить в дереве разложение на простые.
Вот что-то в таком духе, только не в дереве, конечно (это ж лишний логарифм) проходит таки 4 теста из 5 (а на 5м — тл)
ну у меня быстро работало не смотря на возмедение в степень за логорифм, намного меньше секунды на макс тесте. нужно только, хорошо организовать хранение этого разложения... хотя, может, можно как нить свести к поиску максимума в окне с помощью стэка. типа, по каждому простому, но их много конечно...
Утешили, оказалось, я не один такой... Потерял наверно час, чтобы понять, что я у себя уже четко нахожу НОК, зная НОД... но не могу найти НОД, используя модульную арифметику.
У нас следующее решение было. Понятно, что различных простых чисел, на которые делится что-нибудь из инпута, будет не очень много (порядка 10^6 в худшем случае). Для каждого из них заведем multiset степеней, которые входят в текущий НОК + будем поддерживать текущее значение НОКа по модулю. Ну и далее аккуратно удаляем/добавляем по одному числу — перебираем все простые числа, на которые оно делится, обновляем соответствующий multiset и пересчитываем НОК.
А я делал не мультисет, а вектор – степени же простых маленькие, казалось бы должно работать быстро, но не удалось пройти ни одного теста, если у вас сохранился код, можно посмотреть?
Да, конечно. Вот код.
Мы делали так же, но не стеснялись не искать все простые заранее, а хранить map<int,multiset >.
Time Limit Exceeded? Не, не слышали :)
Сдали такое решение. Посчитаем сначала простые до корня из миллиарда. Далее. будем проходить по числам из ввода, и для каждого маленького простого числа считать, с какой степенью оно входит в число из ввода заодно и деля на эти простые. Запомним эти показатели, дальше для них решим задачу минимум на отрезке за О(1), и будем его двигать. Обновим текущие ответы, и продолжим так для маленьких простых. Теперь получим, что каждое число после этого — это либо 1, либо какое-то простое, больше корня из миллиарда. по ним можно пройтись уже мультисетом за один проход.
Значит Java такая Java. У меня было в том же духе
Мы на плюсах это еле затолкали.
Nice contest! :)
Can somebody explain how to solve P2?
We will release the solutions soon :)
I solved it using min cost max flow. At first you make add edge of capacity 1 and weight 0 for each pair of prefernces as well from source to each student. Also we will add edge from each faculty to sink with capacity 1 and weight 1. Then we will find flow of size 1 n times and if all edges from faculty to sink are filled add one more edge with capacity 1 and weight (number of allready added edges from this faculty to sink) + 1
This can be solved with just max flow, without costs. We can initially set the capacities of the edges from faculties to sink to 1, then find the max flow, then increase these capacities to 2, then augment the flow while possible, then increase capacities again etc. A similar problem was in Petrozavodsk once, and this was the author's solution.
Any good source to learn about how to implement max flow(min cost) algo?
В восьмой (поцелуй дементора) динамика по дереву, или какая-то тупая жадность проходила?
У меня несложная динамика по дереву: найдем для каждой вершины
количество вершин в поддереве,
сумму расстояний от нее до вершин в поддереве,
ответ в ее поддереве, если в нее сверху входит путь.
Потом сделаем еще один дфс, поддерживающий сумму расстояний до всех вершин вне поддерева, и для каждой вершины (в предположении, что она верхняя в пути) найдем оптимальную пару детей, в которых спустить путь (просто выбрав два максимума из каких-то величин для детей).
Как решалась 5?
Мы делали следующим образом.
Рассмотрим какое-то число g, такое что 1 ≤ g ≤ k = min(n, m). Найдем, сумму попарных произведений для всех пар чисел (u, v) таких что 1 ≤ u ≤ x, 1 ≤ v ≤ y и gcd(u, v) = g. Сразу будем искать эту сумму деленную на g2. Обозначим ее сумму через f(g). Пусть h(g) = (n / g)(n / g + 1)(m / g)(m / g + 1) / 4. Деление везде выполняется с округлением вниз. Тогда можно записать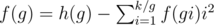 . Последняя формула взята из тех соображений, что h(g) — это количество не только искомых пар чисел, а и тех пар, у которых gcd делится на g. Ответом на задачу является сумма f(g) по всем g, которые не делятся на квадрат простого.
. Последняя формула взята из тех соображений, что h(g) — это количество не только искомых пар чисел, а и тех пар, у которых gcd делится на g. Ответом на задачу является сумма f(g) по всем g, которые не делятся на квадрат простого.
Эту формулу можно посчитать за O(klog(k)). Если в ней явно раскрыть все скобки, то получим следующую формулу: , где m(i) — функция Мебиуса.
, где m(i) — функция Мебиуса.
Теперь заметим, что вне зависимости от n и m в сумме выше каждое h(g) фигурирует в ней с одним и тем же коэффициентом. Значит, можно заранее предпосчитать для всех чисел до миллиона эти коэффициенты и потом их использовать. Теперь решение линейное и проходит 4 теста.
Осталось заметить, что в формуле для подсчета h(g) используются величины n / g и m / g, которые могут принимать не более и
и 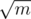 значений, соответственно. Значит, можно посчитать частичные суммы коэффициентов и затем прыгать счетчиком цикла сразу так, чтобы либо n / g, либо m / g изменилось. Выходит препроцессинг за O(PlogP) и ответ на запрос за
значений, соответственно. Значит, можно посчитать частичные суммы коэффициентов и затем прыгать счетчиком цикла сразу так, чтобы либо n / g, либо m / g изменилось. Выходит препроцессинг за O(PlogP) и ответ на запрос за 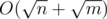 . Здесь P = 1000000. Это проходит все тесты.
. Здесь P = 1000000. Это проходит все тесты.
Здорово). Ни у кого проще не было?
На Java это проходило 3 теста из 5, дальше TL. Зато Катя (моя жена и заодно teammate на этот контест) сумела свернуть это дело дальше. Предрассчитаем две функции, а именно — во-первых, сумму чисел от 1 до i, а во вторых такую хитрую функцию — для чисел, несвободных от кубов — 0, для остальных — пусть pi — те простые, которые входят во второй степени, а qi — те, которые в первой, всего простых k. Тогда . Теперь ответ для x, y — это
. Теперь ответ для x, y — это 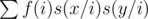 .
.
Это за линию пашет?
По модулю решета Эратосфена — да
Я имел в виду ответ на 1 запрос.
На запрос — да, линия
Круто, у нас линия так и не впихнулась. Пока до корня не соптимайзили, не проходило 5 тест.
Ох, это я читать, значит, не умею :) У нас сначала было ваше решение за nlog, а потом сразу это, которое сразу прошло
Я делал также. На C++ 5 тест ТЛился. Но после всяких оптимайзов удалось это сдать на C.
Получается, что P7 идентична 87C - Интересная игра.
Thanks for a nice contest.
How to do Problem 3? I maintained the maximum power of the primes and when a new number is added I check with the current maximum power, if its more than answer is multiplied by prime raised to difference in power. When a number is removed and this was the number with maximum power, the answer is multiplied by the inverse of prime raised to difference in its power and the new maximum. I have used deque as the data structure.
It got WA. However, I am not able to find any test cases on which the code fails. Here is the code.
Ah, i got the mistake. I didn't kept the prime powers which were greater than 10^5.
Sorry for the trouble.
Solutions to Bitwise 2012 are up! You can view them here: http://www.bitwise.iitkgp.ernet.in/solutions
Hope every1 njoyed Bitwise this year!
Since rudradevbasak is in two of the lists, and he will get the better of the two prizes, then why not slide-up the 11th place holder ?
Even though Rudradev is 4th globally, he is the Indian topper. So he has the option of 10,000 INR or a 16GB pendrive (for global 4th). Its not hard to see that the 10K INR is a better option for him. So we had already slided up the global 21st position
Hope that answers your question.
Omg, we passed problem 1 by solution with Tutte matrix and used all 20 attempts
We used Tutte matrix too. Only 13 attempts though :)
cool, we are not alone :D
We used Tutte. 1 attempt and open this problem.
Did you use a simple approach with a set of prime modulos?
Just one prime modulo.
Unable to view the solutions?