Формулы генерируются со скрипом, надо обновлять страницу, чтобы они появлялись.
Надо сделать, что написано: считать массив и посчитать количество элементов, больших или меньших всех предыдущих. Массив для этого можно даже не хранить, а поддерживать текущий минимум и максимум. Сложность — O(N), хотя проходил и квадрат.
Заметим, что мы всегда можем сперва сыграть все карты с bi > 0, т.к. каждая из них дает хотя бы один дополнительный ход. Количество оставшихся дополнительных ходов после этого не зависит от порядка их отыгрыша. После этого у всех оставшихся карт bi = 0, и из них надо играть те, у которых максимально ai. Простой вариант того же решения: отсортировать все карты по убыванию bi, а при равенстве — по убыванию ai, а затем идти от начала к концу, моделировать счетчик оставшихся ходов и суммировать очки. При этом надо не вылететь за границу массива, если дополнительных ходов больше, чем карт. Сложность — 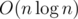 (или O(n2), если сортировать пузырьком, что тоже проходило).
(или O(n2), если сортировать пузырьком, что тоже проходило).
Без ограничения на то, что каждая буква входит не более, чем в одну запрещенную пару, задача становится гораздо сложнее, а в таком варианте работает жадность.
Посмотрим на все вхождения букв из какой-либо пары. Они образуют несколько сплошных подстрок, разделенных какими-то другими буквами. В оптимальном решении две соседние подстроки, разделенные чем-то, не могут <<слиться>> в одну, поскольку для этого нам пришлось бы удалить все буквы, стоящие между ними. Но это никогда не выгодно, т.к. из любой подстроки, состоящей из букв одной пары, всегда можно оставить как минимум одну букву. Значит, нам достаточно устранить конфликты в каждой из таких подстрок, независимо от остальных. Для этого в каждой подстроке удаляем все те буквы, которых в этой подстроке меньше (это оптимально, т.к. пока в подстроке есть хотя бы две разные буквы из пары, где-то они будут соседними).
Все это можно посчитать за O(kN) k проходами по строке.
Здесь тупое решение <<поддерживать список/массив включенных коллайдеров и каждый раз пробегаться и считать все НОДы>> не пройдет по времени, т.к. можно включить в список все простые числа, которых, как известно, 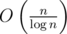 .
.
Заметим, что для каждого числа k, большего единицы, в каждый момент времени включено не более одного коллайдера с номером, который делится на k. Будем хранить массив, i-ый элемент которого содержит 0, если нет включенного коллайдера, номер которого делится на i, либо номер такого коллайдера. При запросе на включение k-ого коллайдера мы можем за 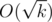 перебрать все делители k, большие единицы, и проверить, что во всех элементах, соответствующих делителям, записаны нули. Тогда конфликтов нет, и можно включить коллайдер, а заодно записать во все рассмотренные ячейки число k. Если же хоть один элемент ненулевой, то в нем записан номер коллайдера, с которым мы конфликтуем, и мы можем его вывести (в этом случае включать ничего не нужно). При запросах на выключение надо просто проставить все нули в ячейках, соответствующих делителям.
перебрать все делители k, большие единицы, и проверить, что во всех элементах, соответствующих делителям, записаны нули. Тогда конфликтов нет, и можно включить коллайдер, а заодно записать во все рассмотренные ячейки число k. Если же хоть один элемент ненулевой, то в нем записан номер коллайдера, с которым мы конфликтуем, и мы можем его вывести (в этом случае включать ничего не нужно). При запросах на выключение надо просто проставить все нули в ячейках, соответствующих делителям.
Все это работает за 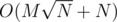 . Можно решать и быстрее, если для каждого числа сохранить список его простых делителей и поддерживать описанный выше массив только для простых чисел. Суммарный размер списков для чисел от 1 до N —
. Можно решать и быстрее, если для каждого числа сохранить список его простых делителей и поддерживать описанный выше массив только для простых чисел. Суммарный размер списков для чисел от 1 до N — 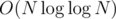 (это следует из оценки на сумму ряда
(это следует из оценки на сумму ряда 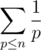 по всем простым, не большим n). Значит, есть решение со сложностью
по всем простым, не большим n). Значит, есть решение со сложностью 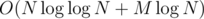 , т.к. количество простых делителей k не превосходит
, т.к. количество простых делителей k не превосходит 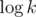 (точная верхняя оценка —
(точная верхняя оценка — 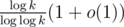 ).
).
Судя по комментариям, самая нестандартная задача. =)
Нужно в графе посчитать количество пар вершин, у которых совпадают множества соседей с точностью до самих этих вершин. Посчитать количество пар вершин, у которых множества совпадают в точности, можно, захешировав эти множества и посортировав хэши (да, хеши — это авторское решение). Как приспособить этот способ для случая, когда между вершинами есть ребро?
Заметим, что таких пар не больше, чем количество ребер, поэтому если мы знаем, как изменяется хэш при добавлении/удалении одной вершины в множество (например, используя полиномиальный хэш строки матрицы смежности графа), мы можем перебрать все ребра и проверить каждую пару напрямую. Можно и по-другому: посчитаем второй вариант хэша для каждой вершины, считая, что в каждой вершине есть петля. Тогда пара множеств будут совпадать как раз тогда, когда вершины — двойники и между ними есть ребро. После этого считаем количество пар аналогично первому случаю.
Можно было сортировать не хэши, а отсортированные списки смежности для каждой вершины. Из-за того, что их суммарный размер — 2M, это тоже могло проходить, но требовало аккуратной реализации, т.к. ограничения были большие. Сложность решения с хэшами — 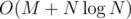 .
.
154D - Флатландское фехтование
Заметим, что если первый игрок может <<убить>> второго за один ход, то и второй из того же расположения (если бы был его ход) может убить первого, т.к. варианты ходов симметричны. Тогда, если нам разрешено стоять на месте, можно применить такую тактику: стоять и ждать, пока противник подойдет. Если он захочет нас убить, ему придется перед этим подойти на расстояние своего хода, после чего мы сразу сможем выиграть. Поэтому, если первый игрок не может выиграть в один ход (т.е. игроки изначально находятся вне зоны досягаемости друг друга), то никто не может обеспечить себе победу, т.к. противник может следовать описанной выше тактике, и в этом случае результат — ничья. Мы полностью проанализировали случай, когда a ≤ 0 ≤ b: если первый игрок может выиграть в один ход, то он выигрывает, во всех остальных случаях — ничья.
Пусть a и b одного знака. Тогда, обозначим d = x2 - x1. Если a ≤ b < 0, мы можем перейти к ситуации (d, a, b) = ( - d, - b, - a), которая аналогична текущей. Поэтому в дальнейшем 0 < a.
Итак, имеем такую игру: есть целые числа d и 0 < a ≤ b. За ход каждый из игроков может отнять от d произвольное целое число из диапазона [a;b]. Тот игрок, после хода которого d = 0, выигрывает. Если в какой-либо момент d < 0, объявляется ничья (т.к. никто уже не сможет выиграть).
Разбираем случай d > 0. Заметим, что если d mod (a + b) = 0, то у второго игрока есть симметричная стратегия: на любой ход x первого игрока он может сделать ход a + b - x, и вернуться в состояние d mod (a + b) = 0. Поскольку d уменьшается, рано или поздно второй игрок выиграет (ситуация аналогична такой же в игре, где можно брать от 1 до k спичек). Итак, если d mod (a + b) = 0, выигрывает второй игрок. Отсюда же, если d mod (a + b) 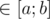 , выигрывает первый игрок, т.к. он может свести игру к предыдущему случаю, предоставив второму игроку ход в проигрышной для него ситуации.
, выигрывает первый игрок, т.к. он может свести игру к предыдущему случаю, предоставив второму игроку ход в проигрышной для него ситуации.
Что можно сказать про все остальные ходы? Оказывается, во всех остальных случаях получается ничья. Докажем это по индукции: пускай d = k(a + b) + l, где 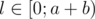 . Ситуация l = 0, как мы уже доказали, проигрышная, ситуации
. Ситуация l = 0, как мы уже доказали, проигрышная, ситуации 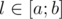 — выигрышные. Если
— выигрышные. Если 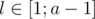 , мы не можем сходить в проигрышную ситуацию (пользуемся предположением индукции для меньших k), но совершая ход a, попадаем в ничейную позицию (если k = 0, мы попадаем в отрицательное число, иначе в отрезок [(k - 1)(a + b) + b + 1;k(a + b) - 1], который по предположению ничейный). Аналогично для l = [b + 1;a + b - 1], ничейный ход — b.
, мы не можем сходить в проигрышную ситуацию (пользуемся предположением индукции для меньших k), но совершая ход a, попадаем в ничейную позицию (если k = 0, мы попадаем в отрицательное число, иначе в отрезок [(k - 1)(a + b) + b + 1;k(a + b) - 1], который по предположению ничейный). Аналогично для l = [b + 1;a + b - 1], ничейный ход — b.
Опять последнюю задачу никто не сдал, хотя некоторые участники подходили к этому очень близко.
В задаче требовалось найти площадь пересечения всевозможных кругов, содержащих заданное множество точек (ясно, что как раз у пересечения площадь минимальна, а количество кругов у нас не ограничено). Для начала поймем, как вообще выглядит это пересечение. Границу этой фигуры составляют некоторые из точек выпуклой оболочки, соединенные дугами окружностей радиуса R. Если мы определим, что это за точки, мы сможем за линейное время посчитать ответ, просто просуммировав площадь многоугольника и площади круговых сегментов.
Определить эти точки — как раз самое трудное. Ясно, что если есть хотя бы одно положение круга, содержащего все точки, с какой-то из точек на границе, то она входит в границу, в противном случае она лежит строго внутри пересечения. Если двигать круг в каком-нибудь направлении, рано или поздно он упрется в какую-нибудь точку — значит, одну точку мы находить умеем. Дальше можно пытаться реализовывать что-то вроде <<заворачивания подарка>> — идти по выпуклой оболочке и поддерживать множество <<граничных>> точек, контролируя взаимное расположение дуг. Однако такое решение связано с множеством технических трудностей и не предполагалось для реализации на контесте (хотя и проходит по времени).
Есть более простое решение, основанное на совсем другой идее. Сперва положим R очень большим, так что все точки выпуклой оболочки являются граничными. Когда мы начнем уменьшать R, точки начнут постепенно пропадать из границы фигуры. Как понять, какая точка пропадет первой? Для точки u из выпуклой оболочки обозначим ее соседей справа и слева l(u) и r(u). Из физического смысла процесса ясно, что первой пропадет та точка u, у которой радиус окружности, проходящей через u, l(u) и r(u) максимален (когда R станет равным этому радиусу, в точке u две дуги сольются в одну, а во всех остальных точках еще будут изломы; такой радиус назовем <<критическим>> для u). После этого удалим точку u из оболочки и будем считать вершины соседними, уже не учитывая ее. Процедуру будем повторять, пока максимальный радиус больше R. Оставшиеся точки как раз и будут точками границы.
Осталось придумать, как делать все это быстро. Заметим, что при удалении точки <<критические>> радиусы окружностей изменяются только для двух соседних с удаляемой. Заведем теперь очередь с приоритетом и будем хранить в ней критические радиусы вместе с номерами точек. На каждой итерации мы извлекаем точку с максимальным радиусом, удаляем ее из оболочки, обновляя информацию о соседях, пересчитываем радиусы для бывших соседей удаленной точки и изменяем информацию о них в очереди. Повторять, пока максимальный радиус не станет меньше R. Опять-таки, поскольку мы фактически моделируем происходящие при уменьшении R процессы, все будет работать корректно. Сложность всего процесса — O(n log n), т.к. итераций не более n и на каждой выполняется константное число операций с очередью размера не более n.
Есть один хитрый крайний случай, а именно когда граничными являются только две точки. Тогда при выкидывании последней точки все три радиуса равны, и наш алгоритм может попытаться выкинуть не ту. Но в этом случае треугольник с вершинами в этих точках тупоугольный, т.к. описанную окружность остроугольного треугольника нельзя сжать, это противоречило бы условию о существовании круга. Значит, надо выкинуть ту точку, угол при вершине которой тупой.










А как пруфятся хеш-решения?
Ну то есть, а что если коллизия, в итоге для взлома отдается не правильный ответ. Это вроде бы не красиво
Хороший вопрос. У нас никак не пруфилось, но мы готовы рассмотреть все случаи, когда это на что-то повлияло.
В свое оправдание могу сказать, что вероятность коллизии полиномиального хэша не превосходит в нашем случае 10 - 12 (хэш по модулю long long'а).
Я могу ошибаться относительно вашего решения, но я так понял, что в качестве хеша испоьзуется одно 64-х битовое число, в таком случае вероятность коллизии много больше чем 10^-12. Вы слышали о "парадоксе дней рождения"? если бы вы юзали примерно 40 битное число, то вероятность коллизии была бы 0.5 на каждом тесте, на сотне тестов 1 — 2^-100, то есть равна фактически единице. Я люблю хеши, и считаю задачи с хешевыми авторскими решениями вполне имеют право на существование, как и другие вероятностные решения, но вероятность нужно оценивать внимательнее.
UPD: более точно, при 64-х битном хеше, вероятность коллизии на одном тесте 0.00000002710503 вероятность коллизии на 100 тестах 0.00000271049905 ~ 3e-6 при равномерном случайном распределении, которое вы не можете обеспечить полиномиальными хешами. Инересующимся советую смотреть википедию, "парадокс дней рождения".
Спасибо за комментарий, я действительно сильно ошибся в оценках, память подводит. =)
В упрощенном варианте оценки выглядят так: пускай мы выбираем равновероятно и независимо M чисел среди N возможных вариантов, а также известно, что M2 / N гораздо меньше единицы. Тогда вероятность коллизии (т.е. что какие-нибудь два числа совпадут) очень близка к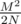 (для доказательства упомянутого Вами <<парадокса дней рождения>> нужно оценивать чуть точнее). В нашем случае M = 106, N = 1018 (довольно грубо), поэтому вероятность коллизии примерно равна 0.5 * 10 - 6, что тоже не так уж много.
(для доказательства упомянутого Вами <<парадокса дней рождения>> нужно оценивать чуть точнее). В нашем случае M = 106, N = 1018 (довольно грубо), поэтому вероятность коллизии примерно равна 0.5 * 10 - 6, что тоже не так уж много.
Да я не спорю, мы в реальном мире живем, а не в идеальном. Я бы не стал заморачиваться даже при двухпроцентной вероятности фэйла, ибо матожидание положительное :)
Но еще раз скажу, и подтвержу, что принимать такое решение за эталон очень не правильно. код расчитывает разные вероятности, по формулам из википедии, и как вы видите в последней строчке вероятность зафейлится хоть кому-либо из решивших, довольно высока, и даже при идеальном хеше соствляет 1.38e-4, и это при 51 одном зачтенном решении, если увеличить ТЛ, со сноской на то что 64 бит маловато, то правильных решений может стать больше, что еще больше увеличит последнюю цифру.
Уже извиняюсь зазанудство :) я тут посчтитал еще, что если бы каждая задача готовилась с вероятностью фейла P, то вероятность фейла среди 110 проведённых раундов из в среднем, скажем 6-ти задач, есть 1 — (1 — P)^ (100 * 6) что уже подходит к десяткам процентов при данных вероятностях :) На деле фейлов было больше, и вовсе не из-за хешей, а просто человеческого фактора, багов в решениях.
Я проверил точным решением :D Во всяком случае, системные тесты. Вот: 1235773
убило в щи :D
Мне кажется, что задачу C можно можно было решать и без хешей, с помощью суфф массива и rmq на массиве lcp=)
а зачем lcp и rmq?
Is there also an English version?
Translation is available when you click on the British flag in the top right of the page. I don't know why it switches to the Russian version when you come from the main page.
I think it's because the link in the previous page is codeforces.ru. If you want to see the english version, go to codeforces.com instead.
В E на контесте мне не показалось понятным, что искомый ответ можно представить в виде подмножества выпуклой оболочки. Иными словами, почему не может так получиться, что есть один критический круг, упирающийся в точки P[1] и P[3], и другой — в точки P[2] и P[4]? Хотя сейчас это как-то смутно осознаётся, но чётко пока не могу понять.
Согласен, не слишком очевидно. Если доказывать, то пускай есть критический круг радиуса R, проходящий через две точки выпуклой оболочки. Тогда минимальный радиус круга, содержащий какую-то точку между ними на своей границе и содержащий обе прежних точки внутри себя, явно больше R, поэтому все точки между ними не на границе.
154A / 155C can also be done in O(N+k) Check out my solution: 1950916
Can someone explain the working of the above solution?I dont get it..
I'll do it, I just need to remind myself what I did, it was 5 years ago! :)
Here's the idea:
We split the input string into consecutive maximal substrings of equal or paired elements. Example:
Pairs are a-b and c-d, the string is "addccbaaebdcdeebabd". The split is: a|ddcc|baa|e|b|dcd|ee|bab|d
Note that we can now process each substring on its own, without interfering with adjacent substrings. The idea is, if we have a substring containing only type of character, we do not modify it, otherwise we remove all occurrences of the character which appears less often.
My implementation keeps track of the state (which is one of the paired characters), and the number (c1, c2) of both types of characters within one substring (if there is only one type of character in a group, one of the numbers will be 0). When transitioning from one substring to another, min(c1, c2) is added to the solution.
Hope this helps!
Ah! I get it now! It's actually a like the solution mentioned in editorial but instead of running through the string k times like the author's solution did,you saved pairs and then did the same thing,reduced complexity to O(n).. Thanks for helping even after 5 years :)
Can anyone explain the kind of Hashing used here http://codeforces.net/contest/154/submission/7343162 Here the hash function is allowed to overflow.Can the same kind of hashing be used for strings? Is the one where we use a Modulus more accurate or this one?
In this case, overflow acts as modulus with
2^64. I think(not sure) it is more accurate since there are fewer chances of hash collisions since I got the wrong answer on test 26 when I used1e9+9for modulo operations in the hash function. submission. Removing the mod operation and allowing the values to overflow led to an accepted solution. submission.Did you get the reason why?