Навеяно 163B - Лемминги.
Предположим, загадано рациональное число, представленное в виде несократимой дроби 0 ≤ p / q ≤ 1. Пусть знаменатель не превосходит Q (в задаче, да и обычно на практике — 109). Есть способ по данному рациональному числу узнавать, больше оно данного, меньше или равно (функция f (p, q) → {1, 0, - 1}). Задача: с помощью вызовов этой функции отгадать загаданное число. При этом функции нельзя передавать числа со знаменателем > Q. Вещественной арифметикой пользоваться нельзя. За какую асимптотику от максимального значения знаменателя (от точности, по сути) можно решить эту задачу? Простому бинпоиску, как мне кажется, этой информации недостаточно — он оперирует значением числа, а не его представлением.
Первое приходящее в голову решение: перебираем знаменатель, потом ищем числитель бинарным поиском. Сложность — O(Q·logQ), что плохо.
Второе решение с использованием ряда Фарея, уже за O(Q), по схеме бинарного поиска. Поддерживаем отрезок, в котором может находиться число, с границами pl / ql и pr / qr, изначально равными 0 и 1 соответственно. На каждом шаге находим pm / qm, где pm = pr + pl, qm = qr + ql, скармливаем это число функции и в зависимости от этого переходим в правую или левую часть отрезка. Из ряда Фарея следует, что мы за не более чем q шагов найдем требуемую дробь. Получили O(Q). Но хочется логарифм или хотя бы что-то сублинейное.
Мне кажется, что я сейчас изобретаю велосипед и что-то такое давным-давно делать умеют. Как можно решать такую задачу?











Здесь описан алгоритм, работающий за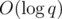 .
.
Спасибо! Похоже, то, что нужно. Завтра попробую вникнуть.
Кстати, а нельзя за быстро найти k-ую по величине дробь вида p/q, p > 0, 1 <= q <= Q?
Гугление по "Order Statistics in the Farey Sequences" что-то выдает...
I happen to know this problem, it is very nice.
I do not really want to spoil it for you, so here is a hint: think of your traversal of the Farey sequence (or equivalently, the Stern-Brocot tree) as a sequence composed of letters L and R. As you noticed in the second solution, the length of this sequence can be Θ(Q), so we cannot just follow it naively.
However, what if the sequence consisted only of Ls (or only of Rs) — that is, if we never changed the direction of our traversal? There exists a faster solution then. Try to generalize it for all sequences.
I've already posted this link in a Russian comment. It describes a solution which works in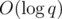 time.
time.