dkjsfkhg's blog

Editorial of Codeforces Round #343 (Div.2)
By dkjsfkhg, 9 years ago, In English

Problem A:

Consider that we have rowi chocolates in the i'th row and coli chocolates in the i'th column.

The answer to the problem would be: 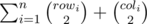. It is obvious that every pair would be calculated exactly once (as we have no more than one chocolate in the same square)

Time Complexity: O(n2)

C++ Solution

Problem B:

Consider that we have boyi males in the i'th day of the year and girli females in the i'th day of the year. These arrays can be filled easily when you are reading the input (See the code). Then for the i'th day of the year, we could have 2 * min(boyi , girli) people which could come to the party. The answer would be maximum of this value between all days i (1 ≤ i ≤ 366)

Time Complexity: O(366*n)

C++ Solution

Bonus: Try to solve this problem with O(n). For each interval given in the input, you don't need to iterate from day ai to day bi. This idea is used to solve problem 276C.

Problem C:

This problem can be solved with dynamic programming:

1. Calculate dpi, j : How many sequences of brackets of length i has balance j and intermediate balance never goes below zero (They form a prefix of a valid sequence of brackets).

2. For the given sequence of length n calculate the resulting balance a and the minimum balance b.

3. Try the length of the sequence added at the beginning c and its balance d. If  - b ≤ d then add dpc, d × dpm - n - c, d + a to the answer.

Time complexity: O((n - m)2)

C++ Solution

Problem D:

First of all, we calculate the volume of each cake: vi = π × hi × ri2.

Now consider the sequence v1, v2, v3, ..., vn : The answer to the problem is the maximum sum of elements between all increasing sub-sequences of this sequence. How do we solve this? First to get rid of the decimals we can define a new sequence a1, a2, a3, ..., an such that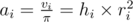

We consider dpi as the maximum sum between all the sequences which end with ai and

dpi =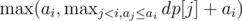

The answer to the problem is: π × maxi = 1ndp[i]

Now how do we calculate 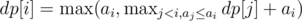? We use a max-segment tree which does these two operations: 1. Change the i't member to v. 2. Find the maximum value in the interval 1 to i.

Now we use this segment tree for the array dp and find the answer.

Consider that a1, a2, a3, ..., an is sorted. We define bi as the position of ai. Now to fill dpi we find the maximum in the interval [1, bi) in segment and we call it x and we set the bi th index of the segment as ai + x. The answer to the problem would the maximum in the segment in the interval [1,n]

Time complexity: O(nlgn)

Thanks to ATofighi who helped a lot for writing the editorial of problem D.

C++ Solution

Problem E:

First of all, we assume that the tree is rooted! For this problem, first we need to compute some values for each vertex u: qdu and quu, cntu , paru, i and hu. qdu equals to the expected value of length of paths which start from vertex u, and ends in u’s subtree and also has length at least 1. quu equals to the expected value of length of paths which start from vertex u, and not ends in u’s subtree and also has length at least 1. to calculate this values we can use one dfs for qd, and one other dfs for qu. \ cntu is the number of vertices in u’s subtree except u, paru, i is the 2i ‘th ancestor of u and finally hu is the height of the vertex u. \ in first dfs (lets call it dfsdown) we can calculate qd, cnt and par array with this formulas:

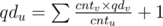
for ecah $v$ as child of u and paru, i = parparu, i - 1, i - 1

in second dfs (lets call it dfsup) we calculate qu using this formula (for clearer formula, I may define some extra variables):

there are two cases:

u is the only child of its parent: let

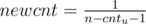
then

\

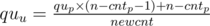
u is not the only child of its parent: let

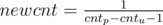
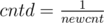
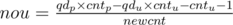
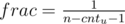
then

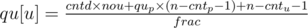
now we should process the queries. For each query u and v, we have to cases: one of the vertices is either one of the ancestors of the other one or not! In the first case, if we define w the vertex before u (u is assumed to be the vertex with lower height). In the path from v to u, the answer is

.

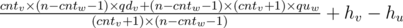
In the second case, if we assume w = LCA(u, v), then answer is

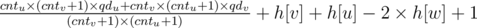
To check if u is one of ancestors of v, you can check if their LCA equals to u or you can use dfs to find out their starting and finishing time. u is an ancestor of v if the interval of starting and finishing time of v is completely inside starting and finishing time of u

The time complexity for the whole solution is O(n + mlgn) (O(n) for dfs and O(lgn) for each query so O(mlgn) for queries!).

C++ Solution

  • Vote: I like it
  • +41
  • Vote: I do not like it

Comments Comments (86)
| Write comment?
»
9 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Thank you for the quick editorial! This is how it should always be. :)

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Shouldn't be the compexity of problem B bonus O(n) rather than O(366)?

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Just wonder if problem C can be solved without the condition n — m <= 2000.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +113 Vote: I do not like it

    I can solve when n — m = 2001.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    The best solution we got was O((n - m)2) time and memory complexity! but for memory limits the n - m cannot exceed 2000

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I think adding codeforces tags to the problem would be more convenient ie.

629A - Far Relative’s Birthday Cake

629B - Far Relative’s Problem

629C - Famil Door and Brackets

629D - Babaei and Birthday Cake

629E - Famil Door and Roads

→ Reply
»
9 years ago, # |
  Vote: I like it +4 Vote: I do not like it

For problem D, you can use BIT(fenwich tree) for simplify.

my solution : 16248220

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I don't understand why everyone used BIT or segment tree in this question. I had a pretty simple solution.

    Submission: http://codeforces.net/contest/629/submission/16246205

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I had a strong feeling that such solution would time out on main tests. I did something similar during contest: http://codeforces.net/contest/629/submission/16246390 Which did tle. But after seeing your solution, a break statement fixes tle http://codeforces.net/contest/629/submission/16254869

      Still wondering what could be worst case running time for such solution

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        The worst case is O(nlogn) only, the same for your solution. Reason — the total number of checks I make to make to delete an element is O(n).

        This will be clear to you if you understand amortized complexity.

        You might be thinking that my solution would be O(n*nlogn) because I might check all elements in every case. but you need to see that if I check t elements in a case, I have already deleted t-1 elements from the set. These t-1 elements will not be checked further in any cases.

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone help me in calculating the following dp table of question C ?
1. Calculate dpi, j : How many sequences of brackets of length i has balance j and intermediate balance never goes below zero (They form a prefix of a valid sequence of brackets).

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it 
    dp(0, 0) = 1
if (j > 0) dp(i, j) += dp(i - 1, j - 1)
if (j < 2000) dp(i, j) += dp(i - 1, j + 1)
    → Reply
»
9 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Solution for B in O(N) if you want to know

629B — 16248917

→ Reply
»
9 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Can anyone explain the binary search LIS solution for D? and provide a source useful to understand the concept behind it ?

→ Reply
»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

I used a BIT to solve problem D and I think my solution is slightly more interesting and different from the one used by others in the respect that I do not do range max queries like described here and I am not sure if this technique is known to a lot of people.

I exploit the property that in a BIT, if we let each node be the max element in the range idx..idx - (2r - 1) where r = LSB of idx, the maximum in range [0, idx] can be simply performed like we perform any operation in a BIT. This won't work for problems where query range is not [0, index] but I have found that this technique is often useful in being able to code Segment tree problems much faster using BIT.

My accepted code is here: 16249272

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I used Fenwick Tree too! But this will work with queries [0, idx] (as you said) and when we need to keep the maximum (or minimum) value so far. If we update some position with a lesser value, it won't work (at least without some tricks)

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      sam721: can you explain this statement:

      If we update some position with a lesser value, it won't work (at least without some tricks)

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Suppose you have this array:

        4 8 2 5

        In this problem you need keep the maximum values seen so far. For example, if you make an update in position 2 (where the 8 is) with a lesser value (3 for example) there won't be any trouble because you know that previously there was an 8.

        But, if you really have to update some position (change completely a number) this approach will not work.

        In this array, the BIT will look like this:

        4 8 2 8

        If you update the second position with a 3, the BIT's 4-th element can't be 8, and it can't be 3 either

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I am not able to understand why we are using max Segment Tree in Prob D. I am not able to visualize this.
I am able to understand the dp equation but how to solve that. Please explain me.

→ Reply
»
9 years ago, # |
  Vote: I like it +2 Vote: I do not like it

You have my deepest thanks. It's really refreshing to see some answers after you finish with the contest. For us (who aren't legendary masters) it's nice to see a good solution to ease our minds. I wish there could be someone to write a some answers for us after each contest.

Thanks again.

→ Reply
»
9 years ago, # |
  Vote: I like it +5 Vote: I do not like it

For problem C instead of DP you can also use the idea behind solving Catalan Numbers by considering a n*m rectangle and calculate the paths...

My code: 16240494

→ Reply
»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Problem D: Can someone tell me if my algorithm is correct? I think there is some mistake in the coding...

my submission: 16248599

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    WA 37 is when you forget the fact that Babaei will put the cake i on top of the cake j only if the volume of the cake i is strictly greater than the volume of the cake j.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 10   Vote: I like it 0 Vote: I do not like it

      I think I didn't forget that... I sorted the volume and when I am updating the seg_tree of for index i then I checked the indices less than i in the sorted list. :(

      By the way, let me check again...

      sorry I didn't notice the word "strictly" ... my bad...

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can someone explain why in C we need to check that d >= -min_balace

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Without this check you'll not pass next sample: 6 3 ))( You solution will count something like ())()(, but obviously balance of prefix must be >= 2 in order to have correct bracket sequence

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain why this code fail in test case 4 ?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    for me counterexample for 4th test was: 6 3 ))(, answer is 1

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      yeah my code fail for this test, i thought that the given string must be valid ( now i don't know why i assumed that :D ).

      Thanks.

      → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

I did a quite simple implementation of Problem D using just Set structure in C++ Standard Library.

Solution: http://codeforces.net/contest/629/submission/16246205

I created a set of a pair of doubles (long long would also suffice) and start processing from the beginning box. The pair contains 1) The volume of the box 2) The volume of the box combined with any smaller boxes previously taken.(initially the volume of the box). When I encounter a new box, I find the just smaller box in the set, and the second value in its pair and add it to the second value in the current pair.

Now, I insert the pair in the set, and go on deleting the next pairs if the second value in their pair is smaller than the second value in current pair. This solution is also O(nlogn) since I am deleting a pair at most once and inserting it at most once. Also, when I encounter a larger pair, I stop. Hence, check is performed at most n times.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    great solution! This is a good idea of using set and greedy methods. But it seems to be not quick enough. What do you think.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      It's not a greedy approach, first of all. And secondly, it has the same complexity as the solution in editorial(Segment Tree) or the other solutions people are mentioning (using BIT).

      The complexity is O(nlogn) for both.

      My way is just easier and faster to implement.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I don't understand why this solution is O(nlogn).

        What is the bound on how many times the while(true) loop executes in some worst case?

        Thanks.

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          In a particular case, the while loop can execute n times ( if there are n elements in the set). This is true. Which can make you think that for n iterations, it will execute n*n times.

          However, it will execute (in total) only n times. Because we are deleting the elements we are accessing in the process.

          This will be clear to you if you understand amortized complexity. You might be thinking that my solution would be O(n*nlogn) because I might check all elements in every case. but you need to see that if I check t elements in a case, I have already deleted t-1 elements from the set. These t-1 elements will not be checked further in any cases.

          → Reply
          • »
            »
            »
            »
            »
            »
            9 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            That makes sense. You are right, I wasn't thinking of the amortized complexity. Thanks!

            → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    can you provide a source explains it in detail. getting LIS using STL in nlogn I mean.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I use the same algorithm like you when I first read the problem. But I got TLE. 17204581 And I found that somebody use the same algorithm but use "map" other than "set",and he got AC.16462759 Now,I know map is much faster than set(maybe just in some case).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 3   Vote: I like it +3 Vote: I do not like it

      You are using the lower_bound wrong. When used in a vector it is used as : lower_bound(v.begin(), v.end(), value). It takes O(logn) time since random access in a vector is O(1). When used in a set it is used as : st.lower_bound(val). If you use it in the set like a vector, it treats the set like a vector. Since the random access of element in a set is O(nlogn), the complexity of lower_bound becomes O(n(logn)^2) instead of O(logn).

      I have corrected this problem in your code, and it is now passing the big test cases. Its however giving a wrong answer later on. You need to correct that.

      New Code: http://codeforces.net/contest/629/submission/17252723

      Also, set takes equal time compared to map. Don't have such misconceptions.

      P.S. I also learned about this behaviour of lower_bound the hard way in a previous contest.

      → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think you haven't handled all possible cases, How can you prove that if an element exist in the set with value less than the current value with me then it shouldnt be looked up again so it can be deleted, Can you explain for me how ur code handle this 1,9,2,3,4,5 If 9 will delete 1 so 2 won't find it so it will start a new sequence at the end it will be 2,3,4,5 instead of 1,2,3,4,5 Suppose these are the volumes, Please if there is something i dont understand correct me

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it +1 Vote: I do not like it

      Step 1: (1,1)

      Step 2: (1,1) (9,2)

      Step 3: (1,1) (2,2)

      Step 4: (1,1) (2,2) (3,3)

      Step 5: (1,1) (2,2) (3,3) (4,4)

      Step 6: (1,1) (2,2) (3,3) (4,4) (5,5)

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain me why my code gets WA in test 37 for problem D? I thought python long integers had unlimited precision, but it seems my code has precision issues http://codeforces.net/contest/629/submission/16250960

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You are outputting the answer in Exponent Notation. When for number 122123, if you output 1.22e5, tester understands 122000, instead of 122123. Its true that python has unlimited precision, but the tester code only sees your output, it does not know that you have calculated the high precision digits accurately.

    Try to print the answer without using Exponent Format. I think it will get accepted.

    → Reply
»
9 years ago, # |
  Vote: I like it +17 Vote: I do not like it

Alternative solution for problem D:

We can solve this problem in a manner similar to calculating the longest increasing sub-sequence(LIS) of an array.

Skip this paragraph if you know how to calculate LIS: To calculate LIS, we maintain a sorted list of elements currently in LIS. Initially add the first element of array to the list. Now when a new element x comes, we replace the element JUST greater than x in this sorted list with x. If x is greater than all elements of list, we append x to the end of the list.

For this problem, we maintain a sorted list of (cylinder_volume,max_total_volume_with_this_cylinder_at_top) pair. Both these values will be increasing in this list. Add the first cylinder to the list. Now when a new cylinder with volume V comes, we find the cylinder with volume JUST greater than V in this sorted list. Let's say it comes at position 'j'. We then insert the pair (V , list[j-1].max_total_volume + V) at position 'j', shifting all subsequent pairs to the right. Now starting from position 'j+1', remove all elements whose max_total_volume value is <= list[j].max_total_volume. The answer is equal to the maximum value of max_total_volume across all the cylinders. Since we need to find, add as well as remove elements in the list, we can use a set<> to maintain a sorted list. Code

→ Reply
»
9 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

On problem C, why is the balance of the suffix d+a? EDIT: OK, got it.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in problem C,why cant the intermediate balance never go below zero. for n="(" and p="" and q=")()" intermediate balance is (-1,0,-1) for q. Is it not?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If you think about building q right to left, you can see that it is the same as building the first string.

    → Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Hi, I'm trying to do D with just STL data structures. It's failing on test case 6, the big one.

Link to code: http://codeforces.net/contest/629/submission/16255422

Any help would be appreciated. I've puzzled over this quite a bit and looked at some other STL based solutions but can't see what's wrong with my logic.

Thanks!!

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    You need to remove some consequent elements in the set to preserve the monotonness.

    → Reply
»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

In problem C can anyone explain how is the balance of q in dp is 'd + b'?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Let balP, balS, balQ be balances of strings P,S,Q. You know that balP+balS+balQ = 0, where balS is a constant and you loop balP in the solution, so let it be fixed. Hence you can calculate balQ = -balP-balS. You know, that balP+balS is non-negative, because it is a prefix of whole string P+S+Q, hence balQ will be non-positive (0 or less). It's also obvious to see it, because while all prefixes of valid round-bracket expressions have to have non-negative balance, the suffixes have to have non-positive balance (just rotate the string to see that). Now the key thing to realize here is, that number of expressions with balance X is equal to number of expressions with balance -X (you exchange "(" and ")"). Hence instead of finding the number of expressions with balance balQ=-balP-balS (which is non-positive), we look for number of expressions with balance -balQ=balP+balS, because these numbers are the same. Now this number -balQ is non-negative, so we have it stored in our dp[lenQ][-balQ].

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Hey thanks for the explanation. Could finally understand how to go about solving the problem after reading this!

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Anyone interested to see his implementation with the idea he (nicely) described can go here

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Now the key thing to realize here is, that number of expressions with balance X is equal to number of expressions with balance -X

      Could you, please, elaborate a bit more on that?

      I don't see that symmetry. I see that all the prefixes P should be non-negative, i.e. all the paths leading to the balance balP cannot have intermediate balance below zero. On the other hand, the intermediate balance of suffix balQ can be positive, that is the paths that arrive at negative balQ can have positive prefix sum.

      Here is an example.

      • We cannot have the following prefix, because it's intermediate state is negative:
        P = ())(
        The balance of P[0..2] = ()) is  - 1, so it is invalid (although P[0..3] is 0).

      • The following suffix Q is perfectly valid, although the intermediate state is positive:
        Q = )(())
        The balance of Q[0..2] = )(( is 1, but it doesn't make it invalid. The whole string might look something like this:
        P = () S = ( Q = )(())

      I will summarize with the following sequences of numbers, showing how the sum changes for prefix P and suffix Q:
      P = ())(( -> (1, 0,  - 1, 0, 1) — BAD
      Q = )(()) -> ( - 1, 0, 1, 0,  - 1) — GOOD

      It looks like there are more paths for the Q than for the P and they cannot share the same dp[prefix_length][balance] table.

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Looks like editorial for C contains error "2. For the given sequence of length n calculate the resulting balance a and the minimum balance b." Should be "length m", not "n".

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What's the idea behind the topdown/recursive solution on problem C?

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I don't seem to get the intuition behind the dp solution of problem C. What does dp[i][j] represent in problem C

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    d[i][j] is number of such strings of length i containing only left and right round brackets such that number of left brackets — number of right brackets is j (= balance of string is j) and any prefix of such strings has non-negative balance (e.g. they can be a prefix of valid round-bracket expression).

    For example dp[3][1]=2, because you can only form strings "(()" and "()(" of length 3 and balance 1. Note that you cannot form a string ")((", because prefix of lenght 1 has balance -1.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I did understand it. But the problem is I am not being able to figuring out the intuition behind this statement:

      dp[i][j] = dp[i-1][j+1] + dp[i-1][j-1];

      I know it works. But dont know why it works?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        If you look at dp[i][j], it is the number of expressions of lenght i with balance j. The last round bracket in such expression(s) is either left or right. This 2 options give 2 subproblems. If the last is left — "(", then the prefix of length i-1 has balance j-1 (because left bracket adds 1 to overall balance) — hence the result of this subproblem is dp[i-1][j-1]. If the last bracket is right — ")", then the prefix of length i-1 has balance j+1, because right bracket subtracts 1 from the balance (and the whole expression of length i has balance j). Putting it together, dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1] — and you just need to handle special cases when j==0 or j==maxBalance-1.

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain what is dm - n - c, d + a in problem C solution? Is it a misprint?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    There is a typo in the editorial, n and m are exchanged. So consider them as exchanged back and matching the problem statement.

    Let's rename the variables: n-m = rem — remaining brackets we need to add, c = lenP — length of string P, n-m-c = lenQ — length of string Q, b = minBalP — minimum balance for string P, d = balP — balance of string P, a = balS — balance of string S, d + a = balQ — balance of string Q

    Note: we need minBalP to open closed round brackets in S that do not have opening brackets in S — e.g. if balance of S is negative, we need at least -balS balance of string P, otherwise string P+S+Q will never be valid.

    Then in the solution we loop lenP from 0 to rem and its balance from minBal to its actual length. For each such string P (there are many of them, but we only care for balance) we consider number of valid suffixes Q — they need to have balance balQ=-balP-balS (because sum of all balances has to be 0). If you check my previous comment you will see why this is the same number as for balance -balQ=balP+balS, so the number of pairs where P has length lenP and balance balP is dp[lenP][balP] * dp[lenQ][-balQ], because lenQ = n-m-lenP = n-m-c (in editorial).

    → Reply
»
9 years ago, # |
← Rev. 8   Vote: I like it +6 Vote: I do not like it

another solution for problem C :

I think my solution is simple and easier to understand more than the solution explained here in the editorial .

16239727

every time we have to add open or close bracket or add the main string (just once)

let L = n-m+1 : n-m brackets to add + main string

DP state is (index , open , taken )

taken : to check if main string taken before or not

open : number of open brackets

lets calculate two values , pre: number of open brackets should be added before main string to make it valid

bef : number of close brackets should be added after main string to make it valid

every time we try to add open bracket and increase (open)

or add close bracket if number of open brackets >= 1 and decrease (open)

or add main string if ( open >= pre and taken == false ) then make open = open — pre + bef

I hope it will help .

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why am I getting RTE. http://codeforces.net/contest/629/submission/16324686

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For the solution of problem C,

I am not being able to figuring out the intuition behind this statement:

dp[i][j] = dp[i-1][j+1] + dp[i-1][j-1];

I know it works. But dont know why it works?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    Every dynamic programming solution can be represented as a Directed Acyclic Graph (DAG).

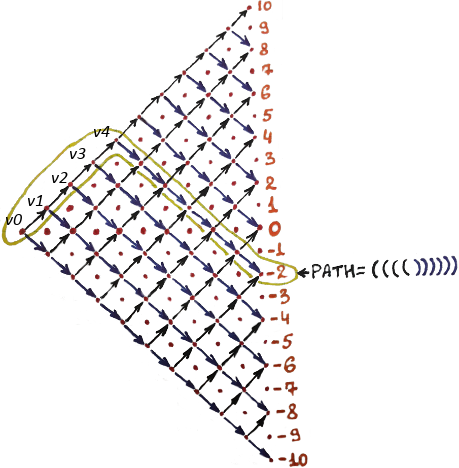
    Imagine the graph in which the edges correspond to parentheses. We can either go up ↑ or down ↓ in that graph (E = {↑, ↓} = {(, )}). Every time we go through some edge, we make a choice of the particular parenthesis. If we go up ↑, that means we have chosen the parenthesis '('. If we go down ↓, it means that we have chosen the parenthesis ')'. As we go along the edges of the graph, we accumulate the parentheses on some string S. Every vertex in that graph corresponds to a state in which we have already chosen the prefix of the string S.

    Let's say, we are on some vertex v4. That means we have already chosen some 4 parentheses:
    S0 = "
    S1 = '('
    S2 = '(('
    S3 = '((('
    S4 = '(((('

    Now we have 2 edges (that means, 2 choices) through which we can go to achieve the next vertex (which we will call v5). Let's say that we have chosen to go down ↓, that is the edge v4 v5 corresponds to a parenthesis ')'. When we move from v4 to v5 we append this new parenthesis ')' to our string S4 and get S5 = S4 + ')':
    S0 = "
    S1 = '('
    S2 = '(('
    S3 = '((('
    S4 = '(((('
    S5 = '(((()'

    The string S5 is the particular path (↑, ↑, ↑, ↑, ↓) through the graph. The path S5 is actually a subpath of the whole path in the picture S = S10 = S5 + ')))))' = '(((())))))'

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why in problem D answer on the second test case is 3983.539484752 instead of 3986.681077? In explanation to the second test case is told that we can use pies with numbers 1,2,4. But it seems that we use only pies with numbers 2,4. WHY???

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I was trying to understand the solution for problem E. I am having trouble with the editorial so I decided to look up on some code.

For no particular reason I chose this one: http://codeforces.net/contest/629/submission/16276620 . But I'm stuck again.

Let's consider the case where LCA(u,v) is not equal to either u or v. Can anyone shed some light on why the answer depends on the product between the number of paths in the subtree determined by u (or v) with the size of the other subtree determined by v (or u)?

Thank you!

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I had in mind the same picture but I cannot figured out what's the connection with the number of paths in a subtree — (why isn't just the product of sizes of the 2 subtrees?).

      Then I thought more about it and figured out that the expected length you're adding to the L[u] + L[v] — 2 * L[lca(u,v)] is equal to the number of paths in the sub-tree. Thank you :)

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

i think solution for question c is wrong as balance could become negative for a prefix due to second string

→ Reply