Domonion's blog

Shortest simple cycle
By Domonion, history, 9 years ago, translation, In English

Undirected weighted graph. For every vertex you should find out shortest simple cycle, which includes this vertex.

I have only O(n ^ 4) solution. Can anybody help me?

  • Vote: I like it
  • +12
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been translated by Domonion (original revision, translated revision, compare)

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

are there negative edges?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    seems like it's not. since it will make this problem NP-hard.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If O(n^3logn) is good enough, for each node, for each edge of the node, remove the edge, run dijkstras to find the distance from the node to the neighbor on the other side of the edge, and add the edge weight to it. The answer is the minimum of these.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Dijkstra's Algorithm does not run in O(N log(N)) time.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I think it's possible to do in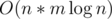 . To compute answer for vertex v, run Dijkstra from it then for every edge w suposse that this edge is included in some cycle of v in the way (where wA and wB are vertexes connected by edge w) and calculate its weight. Answer for v gonna be a minimum of these weights.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    It's also O(n^3 log n)

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it -10 Vote: I do not like it

      No it's not. For each vertex you run dijkstra and check all edges so actually it is O(n * (m + mlogn)). Of course if there will be like n2 edges then it indeed gonna work in O(n3 * logn), but if such constraints exists then n should be quite small.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it +13 Vote: I do not like it

        Your algorithm does not always compute simple cycles. Consider the cycle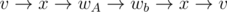 , which is not a simple cycle, but is taken into account by your algorithm.

        → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

please ignore this :(

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Won't work, the graph is undirected, so A[v][v] will be 2x the lightest outgoing edge from v.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I don't know if this is a coincidence or not, but it seems you are not the only one solving this problem: http://research.haifa.ac.il/~raphy/papers/all-cycles.pdf

→ Reply