Ответом на задачу является формула ((a - 1 + b) mod n + n) mod n + 1, где mod n — операция взятия остатка по модулю n.
Итоговая временная сложность решения равна O(1).
Допускается также итеративное решение, каждый раз перемещающее Васю на 1 подъезд в нужном направлении.
Итоговая временная сложность решения равна O(|b|).
Будем рассматривать участников каждого региона отдельно. Отсортируем всех участников из региона в порядке невозрастания баллов. Ответ для данного региона неоднозначен тогда и только тогда, когда участников хотя бы трое и баллы второго и третьего участника совпадают. Иначе ответом является пара из первого и второго участников.
Итоговая временная сложность решения равна 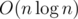 .
.
Наша задача набрать наибольшее количество игрушек, которых ещё нет у Тани так, чтобы их суммарная цена была не больше m. Для этого воспользуемся жадным алгоритмом: будем каждый раз пока нам хватает денег покупать самую дешёвую игрушку, которой ещё нет у Тани. Заведём булевский массив used, чтобы отмечать в нём типы игрушек, которые уже есть у Тани. Очевидно, что на 109 бурлей мы можем купить не более 105 игрушек 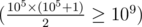 , а значит нам нет смысла рассматривать игрушки с типами больше или равными 2 × 105 (игрушки таких типов из входных данных будем пропускать) и нам хватит массива used размером 2 × 105. Будем идти по типам игрушек в порядке возрастания пока нам хватает денег и, если в массиве used данный тип отмечен значением \texttt{false}, то будем покупать игрушку этого типа.
, а значит нам нет смысла рассматривать игрушки с типами больше или равными 2 × 105 (игрушки таких типов из входных данных будем пропускать) и нам хватит массива used размером 2 × 105. Будем идти по типам игрушек в порядке возрастания пока нам хватает денег и, если в массиве used данный тип отмечен значением \texttt{false}, то будем покупать игрушку этого типа.
Итоговая временная сложность решения составит 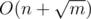 .
.
Если вместо булевского массива использовать тип данных <<множество>> (например, \texttt{std::set} в C++), то можно не пропускать большие значения ai из входных данных. В таком случае временная сложность решения составит 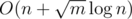 .
.
Из описания трассы следует, что Мария движется таким образом, что вода всегда находится справа от неё. Таким образом, она может упасть в воду только при повороте налево. Для того, чтобы проверить, является ли данный поворот поворотом налево, сопоставим направлениям движения Марии числа: движению на север — 0, движению на запад — 1, движению на юг — 2, движению на восток — 3. Тогда поворот будет поворотом налево, если число для следующего направления dir равно числу предыдущего направления oldDir плюс 1 по модулю 4 (dir ≡ oldDir + 1(mod4)).
Итоговая временная сложность решения равна O(n).
Альтернативное решение. Пусть ответ равен x (это означает, что количество внутренних углов по 270 градусов равно x, а внутренних углов по 90 градусов n - x). Так как сумма внутренних углов n-угольника равна 180 × (n - 2), то можем записать следующее x × 270 + (n - x) × 90 = 180 × (n - 2). Откуда получаем, что 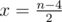 . То есть ответ зависит только от n и не зависит от трассы.
. То есть ответ зависит только от n и не зависит от трассы.
Итоговая временная сложность решения равна O(1).
Во-первых, если граф состоит из нескольких компонент связности, то ответы для них можно считать независимо. Таким образом мы перешли к задаче, когда граф всегда связный. Пусть граф является деревом, тогда мы всегда можем его подвесить и ориентировать все рёбра в порядке обхода dfs'ом. При этом мы сделаем неизолированными все вершины, кроме корня (в подвешенном дереве у каждой вершины, кроме корня, есть единственный предок). Таким образом, ответ в этом случае равен 1. Теперь пусть граф не является деревом, тогда в нём найдётся хотя бы один цикл. Выберем любую вершину на этом цикле и запустим из неё dfs, который ориентирует все рёбра в порядке обхода. Как и в случае с деревом у нас останется только одна изолированная вершина — корень, однако он лежит на цикле и ребро из этого цикла можно ориентировать в него. Таким образом, у нас не останется изолированных вершин и ответ будет равен 0.
Для решения задачи необходимо выделить все компоненты связности и для каждой из них проверить, является ли она деревом. Это можно сделать с помощью dfs или bfs.
Итоговая временная сложность решения равна O(n + m).
В задаче требуется найти связную по сторонам область, произведение количества клеток в которой на минимальное занчение равно заданной величине k. Для этого отсортируем все n × m элементов в порядке невозрастания. Будем последовательно добавлять их в таком порядке, поддерживая при этом компоненты связности. Для этого воспользуемся системой непересекающихся множеств (СНМ, DSU). Кроме того, для каждой компоненты связности необходимо хранить количество клеток в ней. Пусть элемент ai, j только что был добавлен и принадлежит компоненте связности с номеров id. Тогда очевидно, что ai, j — минимум в этой компоненте и если k не делится без остатка на ai, j, то нужной компоненты связности пока получить не удастся. Иначе, посчитаем величину need = k / ai, j — необходимое количество клеток в компоненте связности и если need ≤ CNTid, где CNTid — количество элементов в компоненте связности id, то мы можем найти ответ. Для его поиска запустим из клетки (i, j) dfs, который будет переходить только в клетки больше или равные ai, j и пройдёт ровно need таких клеток.
Итоговая временная сложность решения равна 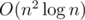 .
.
659G — Забористое разнообразие
Пусть ответ на задачу — это следующая сумма:
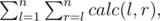
где calc(l, r) — количество способов вырезать верхнюю часть забора так, что её левая граница находится в индексе l, а правая в индексе r. Если l = r (то есть спиливается верхняя часть только одной доски), то calc(l, r) = hl - 1.
Пусть r > l, тогда:
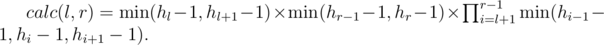
Действительно, число допустимых способов спилить одну доску равно минимуму из высот самой доски и соседних минус один, так как в противном случае нарушится связность спиливаемой части. Крайние доски рассматриваются отдельно, так как у них только по одному соседу. Тогда итоговый ответ на задачу будет выглядеть так:
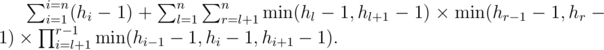
Первое слагаемое вычисляется легко, рассмотрим второе слагаемое. Проведём некоторые преобразования:
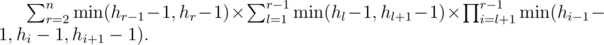
Обозначим
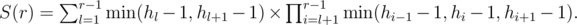
Рассмотрим, как меняется значение S(r) при увеличении r на единицу:
S(r + 1) = S(r) × min(hr - 1 - 1, hr - 1, hr + 1 - 1) + min(hr - 1, hr + 1 - 1).
Таким образом, эту сумму легко поддерживать перебирая r от 2 до n.
Итоговая временная сложность решения равна O(n).










Thanks for nice problems и fast Разбор
Fixed. Thank you)
Интересно, почему в задаче D решение работает за O(N), а ограничения на N до 1000?
Если мозг отказался функционировать, как у меня, можно было взять точку, которая на ~0.5 дальше текущего отрезка, и за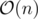 проверить, лежит ли она внутри многоугольника.
проверить, лежит ли она внутри многоугольника.
Вроде очевидная мысль, но мало ли кто не додумался. Как, например, я. Понял эту идею за 4 минуты до конца, быстро написал, без компиляции отправил и... Забыл в цикле одну переменную объявить :)
Thanks for the lightning speed EDITORIAL.
In F problem, I haven't seen the limit that must have an unchanged cell... So I wrote a code in O(sqrt(min(k, 1e15)).. When k > 1e15 print "NO", then enumerate the factor of k, use dsu to solve it, and got WA4. After contest I found the limit and add it then accepted...sad..
The best contest i've seen so far, I really liked the problemset and the fact that is was a 7 problem round instead of the regular one. Great job!
why this 17050130 gets WA in problem E?!!
any one can provide a small case which make it fail ?!
Problem should be solved for every component independently.
I believe this input is a small one where your program fails. There are two connected components: one is a tree and the other is a super well-connected component. The main idea for this test is that the degrees for some vertices are large enough so that when you subtract m edges, then you will not end up with any zeros.
Yea, you don't need to read other comments, better post the same idea that i've already posted but with two times bigger test, good job.
I feel guilty for doing this 17058751 for 659D - Велосипедная гонка:
I simply used
java.awt.Polygonclass to create the lake polygon.If Maria misses turn
i, she would proceed bydx = signum(x(i) - x(i+1)),dy = signum(y(i) - y(i + 1))Then I simply checked if lake polygon contains
(x(i) + 0.5*dx, y(i) + 0.5*dy)Well i guess that's still more ethical than "cout<<(n-4)/2";
Can anybody explain why that is correct?
No idea
It's all explained in the editorial, but:
- assume that for all polygons (convex or concave) the sum of internal angles is 180(n - 2)
- for this problem, there are only internal angles of 270º and 90º and we need to count how many (x) of the former ones exist:
I used ray casting with the same approach...
One line code for problem D using
Point2D.relativeCCW()submission
This one also
Hello everyone , Why testcase 53 is not correct in my answer since my answer totally matched with jury answer here is the link... for problem 2
You have to check if
vec[i].size() > 2before accessing the third element viavec[i][2]. Otherwise you may access unallocated memory. I made the same mistake...Why does this only seem to fail on test 53? Even the first test case has a region with 2 people.
Suppose size is 2. Then suppose that vec[i][0] = vec[i][1]. Then you will look for vec[i][2] to compare with vec[i][1], but that element might not exist (causing Runtime Error). In samples vec[i][0] > vec[i][1], so you didn't need the third element.
There is a parsing error in the editorial of F
А как можно оценить такую штуку (По задаче F). Количество таких a, что k / a >= n * m. Просто не понимаю, случайность или нет, что решение зашло за O((количество таких а) * n * m)).
I solved D by finding point inside a polygon . I had to code almost from the scratch because somehow geeksforgeeks code was not working -_- . And after seeing this O(1) solution.....
Happened with me too !
I found a working code though ( around 7 lines )
Hey,,please give me the link for this code's tutorial
Here You Go :D
Can anybody tell me why i have a WA in test 15 of problem B?
The problem is where you print the answer.
When there are only 2 people in a region the if statement access an irregular position in memory.
I made this check and I got WA in test 15... Can someone tell me why, please?
oh, true! Thank you!
Hello,
sure, it is because you forgot to check size of vector
make the checking line:
if (v[i].size()<3u||v[i][1].p != v[i][2].p)
Thank you!
could you please help me in problem B.I am also facing WA on Testcase 15 . MySubmission 19938161
Here
This modification worked :)
Could anyone help me with that http://codeforces.net/contest/659/submission/17057892 ?
BFS do not check for one cell solution.
My solution for problem D is to count the number of left turn and the number of right turn then take the minimal of them. I have no idea why it works. It was a desperate attempt. Can somebody provide a proof? Thank you!
My submission: http://codeforces.net/contest/659/submission/17055311
My guess is number_of_right_turns = number_of_left_turns + 3
So number_of_right_turns is always greater than number_of_left_turns.
You are actually taking number_of_left_turns.
Just cout << posi << endl; also get AC.
Can someone explain problem F in more detail please? Basically for each cell with value v, you want to know C(v) = how many cells are connected to it that are at least v. When you sort by decreasing value and DSU, won't your calculation of C(v) for cells with the same value be wrong? For example this grid:
2 4 5
6 4 3
I didn't notice that in problem D we may only drop into water on left turn and solved the more generalized version of the problem.
The idea is we can record all the vertical and horizontal segments, and for each turning point we can count how many segments we may intersect if we keep going straight. If the count of segments is odd then this point is dangerous, and not while the count is even.
How does that formula come in problem number A ? Can somebody illustrate please ?
Forget the formula. Basically, all you need to do is to make a loop. When the system has 5 rooms, going 6 rooms front actually means going 1 room front, right? For backward movement, 2 rooms back means 3 rooms front. Just keep adding the number of total rooms until you get a non negative number. So taking mod is enough. Just to avoid 0'th position, as 5%5 or 6%6 makes zero, but you want to print 5 or 6, the mod operation is done in two steps. Eventually the -1 with a and the +1 at the end don't make any difference.
In 2nd Problem, why is the output on terminal and Codeforces Judge different??
I got WA on 1st pretest again and again because of this..
My solution is :- http://codeforces.net/contest/659/submission/17065952
1) You are doing ios_base::sync_with_stdio(0);
2) Then read something C-style: scanf("%d %d",&n,&m);
3) Then read something C++-style: cin>>str>>reg>>score;
Due to 1), 2) and 3) both read same data. I.e. in 3 you read very first input line instead of second.
Hello for problem D, I have a doubt what property does this test case violate:
The first vertex should be the one more in the south and in the west
Thanks!
First of all, thank you for the quick editorial!! I would like to mention 2 points regarding the editorial:
The phrase "as soon as" is used in places where "since" or simply "as" should be used. It is not that important(since the intention is very much clear), but feels odd! :P
For problem E, I did not understand the part "...as chosen vertex belongs to a cycle, at least one of its edge will not be taken to account in the DFS, so it can be given to a root. This way all the vertices will be satisfied." clearly. Can someone explain it in more details?
It is perhaps slightly misworded. The key idea is that for any tree, we can pick any root and direct each of the edges so that only the chosen root of the tree is unaccessible. Therefore, if the program finds a cycle in a connected component, and we assign the root to any node of the cycle then one can perform the same algorithm, except this time there will be one extra edge incident to the picked root (otherwise, the cycle wouldn't exist). This extra edge can, of course, be directed to make the root accessible as well, thereby solving the problem.
So, in short, does this mean the following?
The final answer is the sum of the answers for each individual connected component.
For a connected component, the answer is 1 if the component is a tree, 0 otherwise.
Yes!
У меня небольшая проблема с задачей C. Мои локальные результаты отличаются от результатов теста CF.
http://codeforces.net/contest/659/submission/17051531 — код
C++ я начал изучать недавно, может кто, пожалуйста, объяснить новичку в чем здесь проблема?
Заранее спасибо!
Переменная p не инициализирована. Совет: инициализировать все переменные сразу после объявления. Т.е. не писать int a, b, c, d, а писать int a = 0, b = 0, c = 0, d = 0.
can any one tell why am i getting RTE on problem B
this my submission
Good day to you man!
The RTE is because of sort :'( you have to change comparator:
like this :)
+btw I'm convinced the part at the end is also wrong :/
I would change it like:
Thnx !! it worked !! but i can't understand why RTE ?!
Well, sort comparator must be deterministic.
That means it must decide (in finite time) for each pair of elements, whether one of them is bigger (and which one) or whether they are equal.
a: A < B && !(B < A) means A < B
b: !(A < B) && B < A means A > B
c: !(A < B) && !(B < A) means A == B
anyway A<B && B<A (which could have been returned in your program) is "nothing" so the function could not determine, how to sort it :)
Can someone explain solution for F in more details ?
Problem G has a divide and conquer solution too ... :P *I wanst able to arrive at the formula stated in the editorial but divide and conquer was a bit more intuitive to me *
Link to submission- http://codeforces.net/contest/659/submission/17075860
thanks for your share :) it's very helpful.
can anyone explain solution of problem E in detail.
Every connected component of the graph, could be solved independently. Each connected component has at most 1 vertex with ending degree 0 after all (solving optimally) . If the connected component is a simple path or a tree root on a vertex v, we may notice that this component has 1 vertex with ending degree 0. If the connected component is cyclic, starting on any node we can organize the Edges in order to take no edges with ending degree 0. Imagine we have one conected component witch has a cycle and a path or a cycle and a tree or both :) , for example this: 1-2, 2-3, 3-1, 1-5, 5-6; Notice we can turn it into the problema of the cyclic connected componen. For this, we can also pick the vertex with in-out degree=1 and connect it. For example: 1-2 , 2-3 , 3-1, 1-5 5->6; 1-2,2-3,3-1, 1->5, 5->6; In this phase we have the same cycle! Therefore, we can run a dfs for each connect component and verify if it has any cycle. If it has add the answer by 1, if it has not, add the answer by 0.
If it has a cycle, we should not add 1 to the answer right? your last two lines confuse me
Sorry! You are right! if it has a cycle, we should NOT add 1 to the answer :)
В задаче F зашел DFS от каждой "подходящей" точки, то есть по сути O(m * n * n), где m — это количество — делителей k, которые у нас есть в таблице и при этом с их помощью можно получить объем k. Долгое время в max-тесте был TL, потому что неудачно занулял массив used вершин для DFS. После AC появился вопрос: Количество делителей равное ~3000 это максимум для данных ограничений задачи?
К сожалению, на текущих ограничениях нам не удалось составить тесты против такого решения.
У меня его решение падает на тесте, созданном этим генератором. Можете проверить это на сервере? В запуске проверить не могу, т.к. тест больше 256 кб получается
Нет, при k = 121645100408832000 будет 16760 делителей
Это количество делителей меньших 10^9?
Thanks. Some beautiful problems and elegant solutions out there. :)
There is O(1) solution for problem E. http://www.codeforces.com/contest/659/submission/17067296 Can anyone explain me this.
It's not a real solution. It exploits the fact that many tests cases share the same solution and compares number of nodes, edges and first number in second line to identify the test case and print the solution accordingly.
You can easily hack it! ;)
Means it has weak test cases.
Not necessarily, however, if the problem statement asked to print unreachable nodes it would be way more easier to solve it properly
Please it would be really grateful if someone can explain editorial of Problem F.
You just need to launch dfs from all
iandjthatk % a[i][j] = 0 and k / a[i][j] <= n * m. In dfs count values thatv >= a[i][j]. if value equals to k / a[i][j] you could find answer.Thanks I got your point but if we launch dfs from each i and j for the mentioned condition, won't the complexity be O(n*m*(n*m)) in worst case? How to make it efficient?
You will mark every used points. You can see my solution here
Thanks lord, I didn't realized that the maximum distinct divisors we have to check is really small as n*m<=1e6
Problem G
please explain how S(r + 1) = S(r) × min(hr - 1 - 1, hr - 1, hr + 1 - 1) + min(hr - 1, hr + 1 - 1).
O(1) for bicycle race its superb
Problem E
why N — BPM getting WA?
Graph :
Edge 1 | Node1
Edge 2 | Node2
Edge 3 | Node3
ACed
83363813 can anyone provide a smaller test case where my sol fails
Sorry, I am too late but in problem E, what about individual components with no roads why we have to add 1 as I was getting WA earlier but question states a city is separate only when it has no road leading into it and only leading out of it.
My hand at a more "human" explanation for problem G from someone bad at maths:
First, let's solve this task for constant h[i] (assuming each element of h is reduced by 1 from now on).
If we only consider the first plank, we can cut off any part of plank 0 from 1 to h[0]. The total answer for this plank is h[0] — dp[0] = h[0].
If we consider the second plank, we can either only cut off part of plank 1 from 1 to h[1], or do the same in addition to any possible cutoff ending at the previous plank (it's clear that no matter whether we cut off 1 or h[1], we still can cut off any part of h[0]). The answer for this plank is h[1]+h[1]*h[0], and the total answer is h[0]+h[1]+h[1]*h[0].
We can advance infinitely, storing the answer for the previous plank:
Now let's consider the case where h[i] is non-decreasing.
The start is obviously the same, but things change starting from the second plank.
If we want to cut h[1] but leave h[0] (and everything before) as-is, nothing changes for us, so h[i] is still part of dp[i].
But if we want to also cut off part of h[0] and h[0] < h[1], then we can only cut off any part of h[0] if we also cut h[1] to the same height as we will cut h[0]. For example, if h[0] = 3 and h[1] = 10, we can cut h[0] and h[1] to length 0, length 1 or length 2, but cutting h[1] to length 3 makes h[0] impossible to cut.
This means that in this case:
Finally, let's consider the hardest case — non-increasing sequences.
If we want to cut off h[0] alongside h[1] and h[0] > h[1], then we can only cut h[0] to the same or smaller height as h[1]. If h[0] = 10 and h[1] = 2, we can cut h[1] to 0 (in which case h[0] must be cut to 0 as well), or we can cut h[1] to 1 (in which case h[0] can be cut to either 0 or 1). In addition, all options that depend on h[0] being higher than h[1] are unreachable from h[1].
So in this case, only part of dp[i-1] must be used — instead of dp[i-1], use the same formula as before dp[i-1] but with changed height:
Or, to put it in a different way:
Still pretty convoluted, but hopefully a bit easier to understand. See 223426302