Как решать A, G, I?
P.S. Кому-нибудь еще, кроме нас, пришло в голову в середине контеста уйти в div 2?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
Как решать A, G, I?
P.S. Кому-нибудь еще, кроме нас, пришло в голову в середине контеста уйти в div 2?
| Название |
|---|



В G ответ не зависит от точек и равен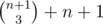 и я не имею ни малейшего представления, почему это правда
и я не имею ни малейшего представления, почему это правда
Но это же неправда. Вот на этой картинке можно выбрать точки A, B и C, а можно D, E и F, но множества будут одни и те же. И ответ будет другой.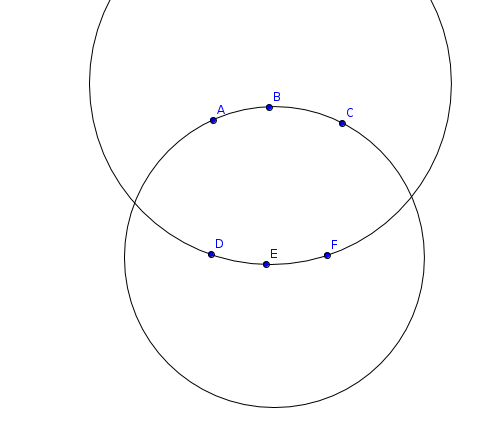
UPD. Я не прав. Ответ на таком тесте сходится. Но совершенно непонятно, почему ответ всегда такой.
На этой картинке легко выбрать круг только с A,B,C, если уж на то пошло. Правда я пока не понимаю связь этого с правильностью/не правильностью решения
Необязательно же брать описанную окружность.
1 + n — пустой круг и круги для каждой точки, содержащие только их.
Для каждой пары точек добавим круг, построенный на них как на диаметре.
Для каждого остроугольного треугольника — описанную окружность, для тупоугольного или прямоугольного — слегка сдвинутую описанную окружность, так чтобы в нее не попадала вершина при тупом угле, а больше ничего не изменилось.
Получается ровно столько кругов. Теперь несложно заметить, что любой круг можно привести к одному из этих непрерывными преобразованиями круга, не меняющими состав входящих точек, а также что все они содержать попарно разные наборы точек.
Разве эти случаи будут попарно различными? К примеру, если на круге, построенном на двух точках как на диаметре, будет ещё одна точка?
Nevermind
Тогда это будет прямоугольный треугольник (угол опирается на диаметр), и окружность, построенная для него, не содержит эту вершину.
Действительно, извиняюсь. Спасибо за подробное доказательство.
Непонятно, почему сдвинутая окружность не будет содержать то же множество точек, как и какая-то другая окружность. На картинке описанная вокруг ABD окружность содержит все 4 точки, чуть сдвинутая от вершины A содержит точки BCD, но эти же три точки содержит окружность, описанная вокруг остроугольного треугольника BCD. (Сорри за рисунок, его мне курица лапой нарисовала)
На картинке описанная вокруг ABD окружность не содержит C по той же причине, по которой описанная вокруг BCD не содержит A — сумма углов BAD и BCD меньше 180 градусов.
На картинке сумма углов не меньше, а больше 180 :) Точку A сдвинул на EPS, а C просто где-то внутри окружности. Ну ок, картинка не контрпример, но вопрос остаётся в силе: почему одна из других окружностей не будет содержать то же самое множество точек?
Довольно короткое, но возможно не самое тривиальное объяснение: выбросим из рассмотрения круги, содержащие 0 или 1 точку, про них все понятно. Пусть два других не равных содержат одинаковый набор точек. Рассмотрим дуги каждой из окружностей, лежащие внутри второй. Одна из них, допустим дуга окружности A, лежащая внутри окружности B, не больше 180. Ни два конца диаметра, ни три вершины остроугольного треугольника не могут лежать дуге меньше 180, а если A описана вокруг тупоугольного треугольника и две вершины при острых углах тупоугольного треугольника лежат на дуге, то и третья тоже лежит, иначе угол при ней острый. Значит A и B не могут содержать одинакового набора точек.
В I если расписать по линейности получается, что nая(начиная со 2) точка приносит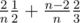 , получаем линейный двучлен от n плюс префикс гармонического ряда, который надо предпосчитать
, получаем линейный двучлен от n плюс префикс гармонического ряда, который надо предпосчитать
Как решать O и M?
M: Вне зависимости от того, как играют игроки, они постараются поднять все фишки, кроме тех, что закрыты той же фишкой, что и единица. Но закрыта единица может быть с двух сторон, поэтому у первого игрока есть преимущество в выборе того, что будет в итоге убрано. Это если кратко, как подробно объяснить без примеров не знаю, поэтому:
Тест:
4 5 6 1 3 2. Здесь есть две закрытые области4 5и2. Помимо их игроки точно уберут 3 фишки, а так как для победы первого игрока нужно убрать нечетное число фишек — он первым ходом откроет область5 4.Тест:
4 1 3 2. Если первый игрок отроет область2он проиграет, поэтому ему есть смысл первым ходом блокировать возможность открытия этой области убрав фишку4.Тест:
6 5 1 4 3 2. Аналогично предыдущему примеру, первый игрок проиграет, если откроет область3 2, но он не может блокировать её открытие вторым игроком, поэтому, допустим, он ходит6, тогда второй игрок открывает область3 2и в итоге побеждает.Тест:
2 3 4 1 7 6 5. Вне зависимости от выбора области2 3или6 5первый игрок проигрывает.Вроде как все случаи разобрал.
UPD: Ошибся с задачей, это M, а не O...
I: заметим, что на k-той итерации вероятность отсутствия перестройки есть матожидание доли листьев в декартовом дереве c k вершинами. Можно написать для матожидания количества листьев реккуренту: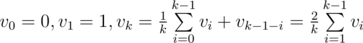 (посмотрели на список вершин, отсортированный по x, нашли максимальное y, оно равновероятно находится в каждой элементе списка, таким образом нашли корень и разбились на левое и правое поддерево).
(посмотрели на список вершин, отсортированный по x, нашли максимальное y, оно равновероятно находится в каждой элементе списка, таким образом нашли корень и разбились на левое и правое поддерево).
Теперь волшебным образом оказывается, что при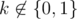 имеем
имеем 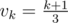 . Действительно, по индукции:
. Действительно, по индукции: 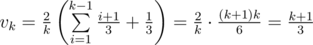
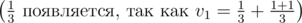 .
.
Тогда ответ есть сумма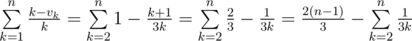 . Последнее можно посчитать при маленьких n и приблизить как
. Последнее можно посчитать при маленьких n и приблизить как 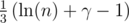 для больших (тогда даже логарифм уже на пределе чувствительность относительной погрешности по отношению к n), где γ — постоянная Эйлера-Маскерони (её также можно найти самому, запустив локально и подождав ответа для достаточно большого n).
для больших (тогда даже логарифм уже на пределе чувствительность относительной погрешности по отношению к n), где γ — постоянная Эйлера-Маскерони (её также можно найти самому, запустив локально и подождав ответа для достаточно большого n).
Как решать H быстрее, чем за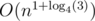 ?
?
А как решать за столько?
Квадродеревом. Нужно провести 2 перпендикулярные прямые так, чтобы 4 части, на которые разбилась плоскость, содержали примерно равное количество точек. Это можно сделать бинпоиском по углу за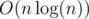 . После этого для каждой из 4 частей запускаемся рекурсивно. Получим дерево. В каждой вершине будем хранить сумму всех точек, которые в ней лежат. Теперь перебираем точку из множества. Все точки, которые можно взять ей в пару, лежат в одной полуплоскости. Заметим, что из четырех квадрантов, на которые мы разбили наше множество, один либо целиком содержится, либо целиком не содержится. Тогда надо рекурсивно запуститься из 3 остальных.
. После этого для каждой из 4 частей запускаемся рекурсивно. Получим дерево. В каждой вершине будем хранить сумму всех точек, которые в ней лежат. Теперь перебираем точку из множества. Все точки, которые можно взять ей в пару, лежат в одной полуплоскости. Заметим, что из четырех квадрантов, на которые мы разбили наше множество, один либо целиком содержится, либо целиком не содержится. Тогда надо рекурсивно запуститься из 3 остальных.
А такое не заходит?
Нет. Хотя, вполне возможно, что проблема в моих кривых руках. Но всё-таки,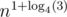 это не сильно меньше квадрата, а константа при этом намного больше.
это не сильно меньше квадрата, а константа при этом намного больше.
тут описана куча решений
Упс, я не видел, что такая задача уже где-то обсуждалась. И не знал, что её можно решать быстрее чем за O(n1.5log). Прикольно.
Расскажите, пожалуйста, как решать D (Subcubes) и E (Super Backpack).
E. Будем добавлять по единичке к сумме, это можно сделать 11 способами.
Остальные способы неинтересны ибо содержат подмножество с нулевой суммой. Дальше вроде понятно, храним по каждой дельте лучших. И пытаемся каждым вариантом улучшить ответ.
code
Классная идея. Авторское такое
Если бы было известно, что ломанные, соединяющие точки (j, a_{i,j}), выпуклы вверх, то мёржить два массива можно было бы за сумму их длин. Тогда применив "разделяй и властвуй", получаем решение за O(nk log(n)).
Оказывается, что результат мёржа нескольких таких массивов удовлетворяет условию: если зафиксировать r и взять индексы j, дающие остаток r при делении на 12, то ломанные, соединяющие точки (j, a_{i,j}), выпуклы вверх. Это доказывается с помощью факта, что если сумма целых чисел по модулю не превосходящих 4 равна 24, то их можно разбить на 2 множества с суммой 12, который доказывается перебором. Предположительно, если 5 заменить на k, то 12 можно заменить на НОК(1,2,...,k-1).
Зная этот факт, можно произвести мёрж за сумму длинн, помноженную на 12, просто перебрав остатки первого и второго индекса при делении на 12. Итого решение за O(nk log(n) НОК(1,2,...,k-1)).
Ещё некоторые умудрились впихнуть такое вероятностное решение. Так же будем мёржить массивы в "разделяй и властвуй", предварительно пошафлив номера массивов. Теперь, когда мёржим два массива, будем смотреть только те пары i, j, которые отличаются мало. Это работает, потому что если разбить множество чисел от 1 до 5 на два равных множества случайным образом, то сумма чисел в первом и втором множестве с большой вероятностью будет маленькой
D. Решение за 2n × m / 64. Разобьем биты на две части размерами k и n - k, для каждого m найдем какие маски из 2k накрываются соответствующим паттерном. Теперь имеем m битсетов по 2k элементов.
Теперь переберем маску из 2n - k элементов и оставим только те запросы, которые ее накрывают. В порядке убывания номеров запросов будем делать OR битсетов и считать количество добавившихся битов.
Чтобы получить AC, построим на бор на масках применяемых запросов и сократим количество действий в m раз. Это проще по коду понять: ideone
Это моя недоработка, что такое решение укладывается в tl. Авторское решение такое.
Придумаем рекурсивное решение за 2^32. сделаем функцию f(msk, i), которая будет вычислять сумму на подкубе msk после i присваиваний. Пусть i-ое присваивание велось на подкубе s и присваивало x. Тогда f(msk, i) = f(msk, i — 1) — f(msk & s, i — 1) + |s| * x. А теперь заметим, что если msk & s всего на одну размерность меньше msk, то можно вместо этого записать. f(msk, i) = f(msk & i — 1) + |s| * x. Этого уже хватает, чтобы пройти тесты. Чтобы получить совсем быстрое решение, нужно ещё заметить, что если что если msk & s всего на две размерности меньше msk, то можно разбить msk & s на два меньших куба и записать формулу через них. Таким образом мы от размерности n переходим либо к размерностям n и k <= n — 2, либо к размерности n — 1.
А можно подробнее про "это проходит тесты" потому, что ровно это у меня (даже с какими-то хаками) не прошло в дорешивание в МФТИ. Говорить, что тут асмиптотика 216 по моему не очень правильно (по крайней мере я доказывать не умею) и кажется, что это вообще неправда потому, что в первом случае первое слагаемое вообще не меняет маску (то есть у нас нет инварианта, что каждый раз количество битов на 2 меньше).
Я тоже не умею доказывать, что это быстро, но у меня есть основания так полагать. В частности, это явно асимптотически меньше 2^m. Кроме того, я потратил очень много времени на составление антитеста, и на худшем из них решение работает 600ms, второе решение на всех тестах работает мгновенно. Я умею доказывать, что мой тест худший из своего класса.
Вот мой код.
первое решение.
второе решение.
Видимо это тест 27. Можешь куда-нить скинуть?
27 тест такой.
http://pastebin.com/U1G5ZnqG
На этом тесте хак с уменьшением хотя бы на два вообще никогда не работает. Если тут асимптотика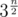 , то у меня не успевает потому, что я на string-ах написал. Не думал, что после этого придётся ещё всё нахачивать.
, то у меня не успевает потому, что я на string-ах написал. Не думал, что после этого придётся ещё всё нахачивать.
Почему неверно, что асимптотика 2^(n/2)*n? Если рассмотреть дерево рекурсии, в нем каждый путь до листа содержит не более n/2 развилок, а значит листьев не более 2^(n/2). Далее, если сжать все пути между развилками, получим 2 * 2^(n/2) вершин. Наконец, каждое сжатое ребро состоит не более чем из n — значит всего O(2^(n/2)*n) вызовов рекурсии.
Это не верно, что каждый путь до листа содержит не более n/2 развилок, так как на развилке лишь в одной из ветвей мы уменьшаем размерность. В частности, на этом примере будет 3^(n/2)
Какое авторское решение в А
Если взять почти сбалансированное дерево с n листьями и взять сумму глубин всех его листьев, то полученное число не будет превосходить n (log_2(n) + 0.08(...)). Поэтому достаточно уметь генерировать сбалансированное дерево с n листьями, чтобы каждый лист был на более коротком расстоянии с одинаковой вероятностью. Если число нечётное, то прибавим к нему 1 и будем решать для n + 1. отсюда (log_2(n + 1) + 0.1). Чтобы таким образом генерировать дерево, можно сделать следующее. Разобьём вершины на пары. После этого некоторые пары схлопнем в 1 вершину так, чтобы получилось степень двойки вершин. на них сделаем сбалансированное дерево. Осталось сделать так, чтобы каждая пара схлопывалась с равной вероятностью. Для этого достаточно брать k последовательных пар, если считать их расположенными по циклу.
Самое классное в задаче G, что многие команды, сдавшие её на 15-20 минутах (и позже кстати тоже) вообще неправильно поняли условие и решали задачу для окружностей, а не для кругов (в том числе команда Вроцлава у которой First to solve по ней).
Неправда, мы доказали решение перед сабмитом, благо доказательство совсем не сложное (ровно как написал Vercingetorix выше).
Извиняюсь за неточность. Как сделать текст перечёркнутым?
textСпс
Разбор задач
Круто. Спасибо!