P_Nyagolov's blog

Rectangle Union Problem
By P_Nyagolov, 9 years ago, In English

Hello everybody,

Today I was solving a problem which reminded me that I still don't know an efficient algorithm for finding the area of the union of large number of rectangles (all rectangles are with sides parallel to the axes). I was looking for a tutorial and the best I found was an article from topcoder which only mentions the existence of such algorithm and presents an O(N^2logN) sweep line + BST algorithm. Can someone please tell me how to solve this faster — O(NlogN) or something like that. I thought about sweep line with segment tree in which I need to update an interval with 1 or -1 and get the number of zeroes over the whole interval but I couldn't come up with a way to do it.

Thanks in advance! :)

  • Vote: I like it
  • +19
  • Vote: I do not like it

»
9 years ago, # |
← Rev. 4   Vote: I like it +3 Vote: I do not like it

You didn't write something or I missed it. Are rectangles parallel to axes? If yes then it's enough to take minimum and maximum in each dimension. Otherwise, I don't understand your idea with 1 and -1 in segment tree (and then you should treat each rectangle as four halfplanes and find an intersection of all 4n halfplanes).

Above, there was some bullshit. I thought that you want to find intersection (instead of union), sorry.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    even if rectangles parallel to axes, it's not enough to take minimum and maximum, because intervals during sweep line might not intersect for example in case of rectangle is above another rectangle (if the sweep line is vertical)

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      if they are parallel you could just take minimum and the number of minimums in the segment

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You can use a segment tree to maintain it. The operations are:

  1. Insert a segment [l,r]
  2. Delete an existing segment
  3. Query the union of all segments

On each segment tree node u, maintain u->tag and u->answer. 

u.answer = (u.r - u.l + 1) if u.tag > 0 else (u.lc.answer + u.rc.answer)

When you insert a segment, just simply increase the tags.

When you delete a segment, just simply decrease the tags.

Do not push down the tags.

About the correctness of this solution, I think it's because of the stable structure of segment tree. When you insert and delete a segment, you always modify the tags of the same nodes (Unlike a BST) which ensure that u.tag is always >= 0.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I think I can solve it in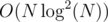 time and 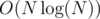space. Let us sort all left and right walls by x-coordinate and see the lenghts of the segments, into which their projections divide x axis. Then build a segment tree on this segments: that is, group 1 and 2, 3 and 4, 5 and 6 etc. and store the lengths of this groups on the next level of the tree, then 1-4, 5-8 etc. All calculations take 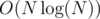time and space. Also for each rectange X it is easy to find a minimal family F(X) (of size 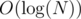) of disjoint segments, associated with the nodes of the tree, which in union give the projection of the rectangle.

Now let us move sweep horizontal line from the top to the bottom: the events are top and bottom walls of the rectangles, which can be easily sorted. In every node of the segment tree we store the free length: the total length of the parts of sweep line, not covered by those rectangles, which don't completely cover the node. For example, free length is the full length of the segment, associated with the node, if and only if each rectangle, intersecting the sweep line, either doesn't cover even a part of the segment or covers it completely. Also in each node we store the list of rectangles X, intersecting the sweep line in the moment, for which this node belongs to F(X). When we add a new rectangle X, intersecting the sweep line, or delete some, these lists are easy to update in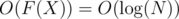 , and free lengths' updates are propagated from the bottom to the top of the tree from each node of F(X) until we hit the root or the node, whose list of covering segments is non-empty. This update totally takes 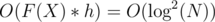time in the worst case, where h is the height of the tree. The area of union between consecutive events can be easily found using the information in the root.

My definition of free length allows to delete rectangles quickly: when the list of bad rectangles in some node becomes empty, we can instantly receive, how much length became uncovered, because it is already written in the node.

→ Reply
»
9 years ago, # |
  Vote: I like it +19 Vote: I do not like it

Am i missing something or is it well known problem?

U can store following for each segment: minimum, amount os minimums; Ez 2 recalculate from childs, fits the idea u described in the last sentence. Should work

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Oh, it should work. Thank you, I feel stupid now :/

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What to do if points coordinates are of the order of 109 ?

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    But will this be o(n log(n))?

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Imagine a set of events , each one is a vertical line at some x coordinate

some of them are the start of a rectangle

and some is the end of a rectangle

between each two events ... the active rectangle are the same and a constant set of y coordinates is covered between each two consecutive events (it doesn't change until another event)

so let's make a segment tree that supports the following operations:

incrementing a range by 1

decrementing a range by 1

and the query is : how many non zero elements are active in the array?

(that means how many y coordinates are active at this moment)

so for each event at coordinate x2 and the previous event is x1

add (x2-x1) * tree.query() to your union area

then update the tree according to this event

the logic of the tree is tricky ....

solving this query problem i mentioned is really hard in general

but here " YOU ARE NOT DECREMENTING UNLESS THERE IS AN IDENTICAL INCREMENTING QUERY BEFORE" because each rectangle is opened then closed

you cannot close a "non opened rectangle" :P

so handing this is really easy (with some probagation)

here is my implementation for rectangle union:

code

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    that's a really cool observation! can you provide more insight on solving the general query problem ? I'm unable to think of any solution other than the naive algorithm.

    → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

hi, I am stuck at a point where i am unable to find out a way in which i can build the segment tree , that can process adding interval,removing interval and querying about the number of non-zero elements in segtree. Can anyone please provide me a somewhat detailed explaination on this. Thank you and sorry for by bad english.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can find number of 0 elements instead of non-zero and (using the fact that all elements are nonnegative) that can be done by calculating by storing the minimum number in the segment and how much minimums are in the segment. If the minimum is zero, then the number of minimums is the number of zeroes, otherwise there are 0 zeroes.

    I think you can figure out the details

    → Reply