You're given N (N ≤ 2000) and N points, then you are given Q (Q ≤ 106), the number of queries, and next Q lines consist Ai, Bi, Ci. For each query you should find how many points are on this line, i.e. how many j that Ai * Xj + Bi * Yj + Ci = 0.
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
18:01:01
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
18:01:01
Register now »
*has extra registration
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 23:33:59 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Suppose we have only one query. (It can be easily solved in O(N) time, but the following approach can be used to solve the initial problem) Let's sort all points by value A·Xj + B·Yj. This is actually sorting in the direction orthogonal to the line. Then we have to find the number of points with this value equal to - C. This can be easily done with two binary searches.
We can see that this solution has two indenedent parts: sorting and answering the query with binary searches. The second can be done in time thus obtainig complexity
time thus obtainig complexity 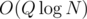 for Q queries. But we cannot sort points Q times.
for Q queries. But we cannot sort points Q times.
To avoid sorting we will do radial sweep (I'm not sure if it is widely used term, if you haven't heard about it, please read this blog ). We will maintain points sorted in some direction and rotate this direction. When the current direction orthogonal to any of the query lines we can answer this query using binary searches. We can see that during that rotation we just need to swap neighbouring points sometimes, moreover, we will do it exactly twice for any pair of points. These moments are when these two points are equal prior to our comparator. This happens if the line containing these two points is orthogonal to the current direction. Now we see that we know for sure in what moments we should do something (answer queries or swap points in the current sorting order). The number of such events is O(N2 + Q). We have to sort them before this sweep.
Overall complexity is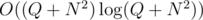
For every two points there is only one line that passes through them. So for every two points you find the line and increase the value cnt[A, B, C]. Now, for each query you can know the value ans*(ans-1) (number of pairs) from cnt[Ai, Bi, Ci]. You solve the equation ans*(ans-1) = cnt[Ai, Bi, Ci] (binary search?) then you have the answer.
Please correct me if I missed something.
Nice one.
The main difficulty is to be able to get the same triple (A, B, C) from every pair of points on one line. Will it be enough to guarantee gcd(A, B) = 1 and A > 0? Let's say that we don't care about horizontal and vertical lines so we assume that A, B ≠ 0. I think it's enough but can anybody confirm?
It doesn't look like a big difficulty. You define:
I'm not sure that
unordered_map<Line,int>works correctly with that, but you can also define operator <, and usemap<Line,int>.gcd(A, B, C) = 1 and first non-zero number of these is positive.
You missed that some given lines pass only through 1 point and some through 0, and this method cannot distinguish these two cases.