Hi guys, I need your help in this problem. it is problem 'K' (subpalindroms) in this contest http://www.codeforces.com/gym/100032/attachments. in the problem a string S with length < 10^5 is given and want us to answer m <3*10^5 queries, each query want us to count the number of palindromic substrings in a given interval. I couldn't find any solution better than O(n^2) although I tried to use hashing and palindromic tree any hint please .. thanks in advance.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.11.2024 19:30:30 (k3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Auto comment: topic has been updated by AzorAhai (previous revision, new revision, compare).
I think this can be solved with Suffix Automata. A similar problem where you have to count substrings of any kind can be solved using this. Not sure about palindromic substring counting though.
You can modify Manacher's algorithm + DP ,and solve it in O(N). I don't know how this works but here you go :
If you only need a hint, don't open this link! http://stackoverflow.com/questions/19801081/find-all-substrings-that-are-palindromes
thanks MedoN11 but the solution in the link solve the problem of counting palindromic substrings in the whole string but my problem is how to count them efficiently in some given range .. do you have an idea how to do so
you could do manacher to get the palindromes and then do mo's algorithm on queries, it will be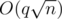
How would I updadte the count when extending/shrinking the current intervall?