Сегодня в 20:00 по Москве будет сабж продолжительностью 2.5 часа.
Допускаются все, кто вышел из квала, но ещё не прошёл в раунд 2.
В раунд 2 выходят топ1000 участников.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.11.2024 13:24:14 (l2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Как решать С large?
Можно понять что ограничение 500 на самом деле это просто запутывание. В массиве можно оставить только 46 наименьших а дальше meet-in-the-middle.
Прикольно. А не долго получается, как я понимаю у тебя 3^23 на log3^23 ?
Поэтому я и не сдал. На хорошем компе с хешмепами может и пройдёт.
Тут же еще 3^23 long long надо хранить. У меня прошло когда рассматривал 28 наименьших.
А что если первые 46 чисел будут такие: 1 2 4 8 16....?
На самом деле можно даже не наименьшие брать а любые и все равно получается 2^46 > 46 * 10^12
Как писать meet-in-the-middle тут? Хотел просто посмотреть решение, но homo_sapiens не нашелся.
Там хендл не может содержать подчеркивание, поэтому точка. На самом деле я её не сдал потому что это медленно, надо еще немного подхачить
А можно пояснить почему надо брать только 46 наименьших(любых) чисел?
Максимальная их сумма: 46*1e12, кол-во подмножеств: 2^46, далее приницп Дирихле
Просто генерируем рэндомный вектор из 10 чисел из набора и так до тех пор, пока не найдем две одинаковые суммы. Я зафейлил эту задачу, считывал числа как int :) Но, когда заметил — оутпут на large генерирует где-то за полторы минуты.
Т.е. размер каждого вектора из ответа не превосходит 10?
Я генерировал ровно по 10 элементов. В среднем нужно было около двух миллионов итераций. Можно сделать оценку, почему это должно работать. Это как парадокс дней рождения — с какой вероятностью среди случайных чисел найдутся два одинаковых.
В целом, сочетаний из 500 по 10 порядка 1021, а максимальная сумма 10 чисел лишь 1013. Понятно, что совпадений очень много.
Даже шести
Вопрос снят, понял почему
У меня зашла такая байда: генерим около 10^7 рандомных подмножеств из первых 250 чисел и запихиваем полученные суммы в хэш-таблицу. Потом рандомно выбираем подмножества из других 250 чисел, пока не найдем с какой нить суммой, что есть в хэш-таблице.
Ну, какой нить механизм восстановления подмножеств по сумме придумать не сложно. Я, например, сохранял 40000 случайных перестановок в массивчиках, а в хэш-таблицу складывал суммы по всем префиксам вместе с номером перестановки.
Оно искало ответы чуть больше 5 минут.
Я делал так: возьмём два простых числа p и q, p чуть меньше 2^20, q чуть меньше 2^25. Разобьём исходный массив на 25, по 20 элементов в каждом. В каждом таком маленьком массиве найдутся две одинаковые суммы по модулю p. Получаем массив из 25 пар. Посмотрим теперь на них по модулю q. Посчитаем 2^25 сумм (из каждой пары берём одно число). Получим две одинаковые по модулю q. Ясно, что эти суммы совпадают по модулю pq. pq несколько меньше, чем 500 * 10^12, но и этого хватает.
А я генерировал в порядке возрастания все возможные суммы и ждал пока повториться хоть одна — за минуту все 10 тестов успело сделать :)
Моё решение (см. комментарий ниже) отработало меньше чем за секунду.
Я тоже довольно долго думал над этой задачей, и в итоге пришел к решению. Понятно, что из 48 чисел есть 2^48 возможных подмножеств, а их максимальная сумма 48*10^12 т.е. подмножеств в несколько раз больше(в 5.6 раз), чем максимальная сумма. Я рандомно перемешал массив, для первых 24 чисел сгенерил всевозможные маски, посортил по сумме пары (сумма, маска), для чисел с 25-ое по 48-ое проделал тоже самое. теперь генерим случайно два индекса в обоих массивах, и пытаемся двумя указателями найти эту сумму в массивах, если нашли и индексы не совпали, то мы молодцы, иначе снова генерим индексы. Такое решение у меня зафейлилось на чем-то, я успел отдебажить и закончить тесты до окончания времени, время работы было около минуты, у меня 4гб оперативы на ноуте, прога должна была жрать около гига, но все влезло. Интересно было почитать другие варианты решений, потому привёл свой.
Вопрос снят
Почему в B мог валиться обход в ширину из всех клеток, куда можем пройти до начала ухода волны?
может залазил туда, где нельзя залезть(типа места мало, но сильно выше уровня моря). А вообще проще было это тудаже внутрь дейкстры пихнуть
Потому что там время перехода может зависеть от глубины. Кроме того, для каждого перехода нужно вычислять момент времени, когда по нему можно начинать идти. Обход в ширину не умеет решать такую задачу. Я думаю, что простейшее решение всё-таки будет с Дейкстрой.
Так я это вроде учитываю — пихаю начальные вершины в очередь и пока она не пуста пытаюсь улучшить время до всех соседей (учитывая глубину/время прихода/etc), улучшил — добавил в очередь. Должно же работать.
а есть что нибудь типа дорешки? а то я кажеться у себя нашла ну ооочень обидную багу в В =(
Просто
добавь водызайди в контестспасибо я идиот забыла проверить, что нельзя идти в комнату, в которой расстояние между потолком и полом < 50 теперь задача заходит(((
http://code.google.com/codejam/contests.html
Я решал C таким образом: запускал рюкзак до двух миллионов, если ответ не находился, то сортировал числа и переходил к попарным разностям (если числа были i1, i2, ..., in, то новые числа будут i2 - i1, i4 - i3, ...,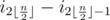 ) и пытался ещё раз, так повторял, пока не находил ответ. Как доказать, что это работает, я не знаю, но работает достаточно быстро.
) и пытался ещё раз, так повторял, пока не находил ответ. Как доказать, что это работает, я не знаю, но работает достаточно быстро.
Мне сейчас вспомнилось Ваше решение задачи про разбиение гиперпространства гиперплоскостью (Петрозаводск, контест MIT). Как у Вас получается постоянно придумывать решения из серии "а оно ведь работает"?
Не знаю. Наверное, мой мозг работает по такому же принципу.
Кстати, если я правильно понимаю, о какой задачке из Петрозаводска вы говорите, то это — "построить линейный классификатор, который не ошибается на выборке, при условии, что выборка линейно разделима". Кажется, они написали что-то вроде градиентного спуска для вектора весов. Так вот, есть теорема Новикова(http://www.machinelearning.ru/wiki/index.php?title=%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%9D%D0%BE%D0%B2%D0%B8%D0%BA%D0%BE%D0%B2%D0%B0) о том, что если взять правильный шаг для градиентного спуска(правило Хебба), то процесс сойдется и, более того, за конечное число шагов. Это я всё к тому, что, кажется, правильность решения в Петрозаводске все пытались объяснить слабыми тестами, что на самом деле, видимо, неправда, и решение абсолютно честно получало AC.
Из раунда 1C. КАК?
Отправил не тот исходник на маленькую задачу и вовремя об этом сообщил.