Пусть у нас есть множество A, которое состоит из m целых чисел от 1 до n (будем считать, что 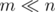 , например, что m = no(1)). Мы хотим построить структуру данных, которая по числу будет определять, лежит ли оно в A. При этом, у нас будет жесткое ограничение: на каждый запрос алгоритм должен смотреть лишь на один бит структуры.
, например, что m = no(1)). Мы хотим построить структуру данных, которая по числу будет определять, лежит ли оно в A. При этом, у нас будет жесткое ограничение: на каждый запрос алгоритм должен смотреть лишь на один бит структуры.
Какого минимального размера структуры можно достичь:
если алгоритм должен всегда выдавать верный ответ,
если алгоритм может ошибаться с вероятностью 1 процент (но при этом должен выдавать верный ответ с вероятностью 99 процентов для любого запроса)?











В 1 ответ наверно 2^n. А 2 немного похоже на PCP теорему. Наверно в 2 ответ poly(m,n):)
Оба раза попал пальцем в небо.
Выбирая, на какой бит смотреть, алгоритм знает n и m?
Да, знает. n, m и запрос.
Возможно, я что-то не понял. В первом наверное правда 2^n и непонятно, как использовать условие m << n. Во втором можно сделать что-то похожее на хэш-таблицу, не обращая внимание на коллизии (то есть, считая, что их нет). То есть все числа заменяем на хэши и сводим к первому пункту, взяв в качестве n длину диапазона значений хэш-функции. Если хэш будет принимать не меньше S = 1 / (1 — 0.99^(1/m)) значений, то вроде бы вероятность ошибки будет не больше 0.01. В качестве хэш-функции можно взять остаток по модулю S — она будет достаточно равномерной, поскольку m << n. Как-то так.
UPD: в первом все-таки не 2^n а n бит. А во втором, соответственно, S бит.
"должен выдавать верный ответ с вероятностью 99 процентов для любого запроса"
Для запроса, попадающего в коллизию, неверный ответ будет с вероятностью 100 процентов. Не подходит.
"В качестве хэш-функции можно взять остаток по модулю S — она будет достаточно равномерной, поскольку m << n."
Равномерность никак не следует из условия m << n. Хоть все элементы могут иметь одинаковый остаток от деления на S.
Хм, да, вы правы. Я считал, что запрос случайный. Как и сами числа из множества.
А что если так. Берем не один модуль, а 100: S1,..., S100. И пусть они все будут попарно взаимно простые и не меньше sqrt(n). Для всех чисел во множестве считаем остатки по каждому модулю. А для запроса считаем остаток по одному случайно выбранному модулю (из этих ста). Коллизия может быть максимум по одному модулю, поэтому попадем мы на нее с вероятностью 0.01. Вот только размер структуры получается довольно большой — чуть больше 100 * sqrt(n), и условие m << n никак не используется.
И есть такие запросы, для которых вероятность < 99%.
Почему?
Что-то я похоже неправильно понял, и не заметил "Коллизия может быть максимум по одному модулю".
А почему коллизия может быть максимум по одному модулю? )
Если коллизия хотя бы по двум, то по КТО коллизия так же и по их произведению. А оно больше n, так что равенство остатков значит равенство чисел. Противоречие.
Потому что числа, сравнимые по двум взаимно простым модулям, сравнимы по модулю их произведения, которое в данном случае больше n.
Может получиться, что нам дали элемент не из А, но у него есть коллизии со всеми элементми из А, с каждым по своему модулю. Так что нам надо не 100 модулей, а 100*m. В остальном мне нравится :)
Да, точно:) И тут как раз оказывается полезным то факт, что m << n
А можно чуть подробнее решение расписать, чтобы понятно стало?
Выбираем натуральное число К > 1. Выбираем 100 * m * (K-1) попарно взаимно простых натуральных чисел S[], бОльших n^(1/K). Для каждого S[i] заводим S[i] бит, в которых запоминаем, какие вычеты по модулю S[i] встречаются во множестве.
Пусть есть запрос Х. Берем его остаток по случайно выбранному из S[] модулю. Смотрим на бит, соответствующий этому остатоку и этому модулю. И отвечаем на запрос значением этого бита.
Если X принадлежит множеству, то ответ будет верным в любом случае.
Пусть Х не принадлежит. Тогда мы смотрим на один из 100 * m * (K-1) бит, соответствующих остаткам X по модулю каждого S[i]. Предположим, что среди них более чем m * (K-1) содержат значение True. Тогда найдется число из нашего множества, которое сравнимо с X по K попарно взаимно простым модулям (которые больше n^(1/K)), поэтому X само должно принадлежать множеству, а это неверно. Значит, у нас есть не больше m * (K-1) бит, содержащих значение True, поэтому положительный (т.е. неверный) ответ мы в этом случае дадим с вероятностью не больше 0.01.
Получается около 100 * m * n^(1/K) * (K-1) бит. Как выбирать K al13n написал ниже.
Если взять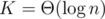 , то n1 / K = O(1) и тогда нам придется взять в качестве модулей первые
, то n1 / K = O(1) и тогда нам придется взять в качестве модулей первые 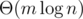 простых. Их сумму можно оценить так:
простых. Их сумму можно оценить так: 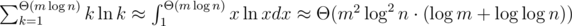 .
.
Так что вроде ваше решение не работает.
Впрочем, решение размера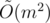 тоже вполне себе интересно. :)
тоже вполне себе интересно. :)
А если sqrt(n) заменить на n^(1/K), получится, что достаточно порядка 100 * m * n^(1/K) * (K-1) бит памяти. При К порядка log n получается ответ всего O(m * log n). Здорово. Осталось доказать, что меньше не бывает. UPD: это неверно, см. выше.
Нижняя оценка очевидна: для разных множеств структуры должны быть различными.
В 1-ом вроде кэп, там от m вообще ничего не зависит.
Мы задаем какой-то вопрос структуре, она отвечает нам либо "Да", либо "Нет", посмотрев в какой-то соответствующий бит. Значит каждый бит должен отвечать за ровно одно число (иначе нам нужно > 2 вариантов ответа). Значит ответ — n.
Думаю, фишка в том, что бит не обязательно отвечает за одно число. Например, чтобы поставить в соответствие запросу какой-то бит (на который мы будем смотреть), мы можем использовать какую-нибудь случайную величину. И тогда одному и тому же запросу не обязательно каждый раз будет соответствовать один и тот же бит
Разве тогда мы сможем всегда получить правильный ответ?
Ведь если да, то логично, что всегда можно смотреть на один и тот же бит.
upd: Я может не совсем понятно написал. Я имел ввиду что только в 1-ой задаче от m ничего не зависит. Исправил.
Правильный — нет. Правильный с вероятностью 99% — почему нет?
"1. если алгоритм должен всегда выдавать верный ответ". Я написал только про это, про 99% я ничего не утверждал :).
А, все, я извиняюсь:) Я думал, второй абзац относится ко второму пункту
Не про это ли рассказывал Андрей Ромащенко на колмсеме в прошлом году (http://arxiv.org/pdf/1102.5538) ?
Offtopic: что за дурацкая привычки давать ссылки на pdf'ки Архива? :)
offtopic: в данном случае это не моя привычка — ссылка скопирована из сьма. А править неудобно, ибо с планшета.