Сегодня прошёл 6 этап Открытого Кубка.
После окончания тура предлагаю здесь обсудить задачи.
UPD: Уже можно обсуждать.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 159 |
| 5 | atcoder_official | 156 |
| 6 | djm03178 | 153 |
| 6 | adamant | 153 |
| 8 | luogu_official | 149 |
| 9 | awoo | 147 |
| 10 | TheScrasse | 146 |
Сегодня прошёл 6 этап Открытого Кубка.
После окончания тура предлагаю здесь обсудить задачи.
UPD: Уже можно обсуждать.
| Название |
|---|



А когда дорешка откроется?
Логично, что не раньше окончания альтернативного тура.
пишут — их проблемы. как решать I?
По-моему, у них итак нет такой проблемы, только плюс)
Если мы начнём тут обсуждать, то будут подсказки как бы :)
Да и к тому же, обычно альтернативное время — на день раньше основного тура, те, кто пишут в альтернативное время, не начинают же обсуждать задачи раньше окончания основного тура.
а они не могут разве посмотреть задачи?
Кто они?
если они будут смотреть задачи, то
(c)AguL
Нигде снаружи условия вроде не выложены, они пока доступны только в системе. Так что не читеря внаглую (вроде "одолжить условия у друзей") — не могут.
Во втором дивизионе произошла, мягко говоря, интересная ситуация:
Команда Vilnius U Data Killers: Siozinis, Ziukas, Smicius сдала задачу M в 0:00. Хоть эта задача довольно простая, всё же я думаю, что потратить меньше минуты на чтение условия, написание кода и его отправку — сложная задача даже для топовых участников.
Я понимаю, что эта ситуация в турнирную таблицу особых изменений в турнирную таблицу не внесла, но эта команда отобрала седьмой зелёный квадратик у команды Samara SAU Teddy Bears: Glaschenko, Dergunov, Semushin.
Координаторы несут какую-то ответственность за несвоевременную выдачу условий?
А вам не кажется палевом то, что вы сказали, что задача M простая?
Отчасти, конечно, это палево.
Но я думаю, что если команда, видя монитор, до сих пор не решила M (прошло 3.5 часа), то и моё "палево" им не поможет.
Хотя, конечно, лучше бы я так не делал.
Заминусуйте себя.
Мне все это странно, так как если команда уже решила нарушить правило, что нельзя пользоваться интернетом кроме как для связи с сервером открытого кубка, то в качестве "как бы еще почитерить" они что-нибудь более существенное придумают, чем прочитать, что задача M — простая
СЖЕЧЬ ЗА ЗЕЛЕНЫЙ КВАДРАТИК!
21:00 прошло — дорешивание нам!
Как решались A и D?
Хором спросили)
Какое наиболее простое решение есть в задаче D и как решается A?
В D придумали некоторый онанизм с методом Гаусса, который вряд ли зайдёт по TL (всё-таки 27 * 10^9 пусть даже делённый на 32 и на константу Гаусса — не, там дальше ещё много операций...)
В А ничего похожего на решение не придумали.
В А очень хитрая динамика, мы на контесте написали, но в одном месте затупили и не отдебагали=(
Если в дорешку зайдет, то рассажу=)
В A, насколько я помню, авторское решение работает за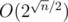 . Автор задачи — Вася Астахов, можно подробнее спросить у него (ну или я вспомню и напишу). Есть также кубическая динамика, но она медленнее работает :)
. Автор задачи — Вася Астахов, можно подробнее спросить у него (ну или я вспомню и напишу). Есть также кубическая динамика, но она медленнее работает :)
Почему я не удивлён? :-) А где у него можно спросить?
На кодфорсес он редко бывает, так что разве что лично :) (для участников яндекс-тренировок это просто). Если очень интересно и не хочется ждать — могу попробовать вспомнить (там несложно было, по крайней мере, если знать итоговое время работы).
Я пока к Яндекс-тренировкам не имею отношения, поэтому хотел бы узнать сейчас. Вспомнишь, если не трудно?
У меня в дорешке кубическая динамика получает ва 7, но стресс для небольших чисел совпадает, ушел дебагать...
По модулю не брали в одном месте. :) Рассказывай!
http://codeforces.net/blog/entry/4505
Я написал разбор задачи А динамикой, если надо=)
В D именно что Гаусс деленный на 32. У нас запускался как минимум 2 раза и при этом летал на случайных тестах с n = 3000.
Как, ну как, объясните мне 3000^3 / 32 могут работать меньше 1 секунды? Там даже break вставить некуда...
На Java ;) На самом деле там еще пополам делится. В общем-то получается пол-миллиарда операций xor с элементами массива, которые в кеш помещаются — поэтому и быстро!
А почему тогда нельзя поставить N до 1000? Ну или если куб так быстро отработает, то хотя бы 2000.
Просто мы на контесте придумали решение с такой ассимптотикой, но на джаве со встроенными битсетами получили тл просто считая определитель и расстроились.
А потом все пытались придумать решение с лучшей ассимптотикой, но ничего не вышло.
Пол-миллиарда даже, Сережа. :) А Java умница в таком случае.
Ой, не то написал :) Исправил.
В общем-то чего ей тормозить на обычных арифметических действиях? Разве что проверка выхода за пределы массива...
А как получить СЛАУ в Д?
СЛАУ тут нет. На задачу можно посмотреть с такой точки зрения — надо инвертировать l бит в матрице над Z_2, чтобы ее строки стали линейно независимыми, что эквивалентно нечетности исходного определителя. И в такой постановке уже плясать.
Теперь понятно:) В голову пришла идея только получить максимальную ЛНЗ систему, а потом уже у оставшихся ЛЗ векторов инвертировать биты (сначала по диагоналям, а потом по строчкам). Можно поподробней? :)
Решение есть, если L >= N — ранг матрицы.
Алгоритм:
Берем последний столбец.
Если в нем все 0, инвертируем последний бит последней строки.
Иначе меняем местами последнюю строчку и какую-нибудь, где 1, и в случае N = L инвертируем какой-нибудь другой бит. Xor-им остальные строки, где последний бит 1, с ней.
Уменьшаем N на 1.
Когда N = 3, решаем перебором.
Мы решали так. Проводим Гаусса, находим ранг, если в каком-то столбце нет ведущего элемента — добавляем его, просто меняя какой-то бит в этом столбце. Если нам не хватило до полного ранга — No solution.
Теперь у нас есть матрица с определителем 1 и надо поменять оставшиеся биты так, чтобы определитель остался 1. Можно делать это случайным образом с проверкой, поскольку вероятность того, что случайная матрица невырождена, достаточно велика.
http://codeforces.net/blog/entry/4505
Я написал разбор задачи А, если кому надо=)
Как решать B,C и F?
B — жадно. Будем на каждом ходу очищать самый ненужный погреб. В первую очередь это такой погреб, где хранится вино, которое уже никому не нужно, т.к. категории для него закончились и оно просрочилось. Если такого нет, продадим самое молодое вино, такое, что если мы его продадим, из этой категории еще что-то останется. Если и такого нет, выводим 0.
P.S. Условие к этой задаче писал наркоман, я гарантирую это.
То, что в правке, неверно. :/ Но, наверное, идею можно развить.
B — В каждый год нужно хранить для каждого погреба, сколько лет вину, которое там храниться. Соответственно, когда проходит один год — нужно увеличить на 1 значения во всех погребах, при этом на каждом шаге нужно найти погреб, в котором сейчас проходит "смена поколения" вина, а из таких взять тот, в котором самое древнее вино и заменить его на новое, если чуть-чуть подумать, то окажется, что за счет делимости длительностей друг на друга, у нас все погребы, в которых происходит смена поколений, на этом шаге увеличат свое поколение на 1, но тот, который из них самый древний станет 0.
C — простой разбор. Понятно, как строится выражение. Берётся название переменной и к ней последовательно дописываются *, () и []. В обоих выражениях строим последовательность применений операций, напрмимер, рекурсивно разбирая каждое выражение. Потом в первом выражении убираем последние столько операций, сколько выполняется во втором и выводим, опять же, рекурсивно то, что осталось от первого выражения.
Коряво как-то получилось, но суть такая.
На самом деле второе выражение разбирать незачем, достаточно посчитать сколько раз в нем встречается *, [] и (). Еще облегчает жизнь подробное описание алгоритма разбора объявления переменной. Нужно просто накодить то что там написано, параллельно затирая первые k операций над переменной, после чего убрать лишние пробелы и вывести.
Там можно вообще читерски ничего не разбирать.
Удаляем везде пробелы. Во втором выражении считаем суммарное число символов
'*', '[' и '()'. Назовём его m. Потом в первом выражении находим имя переменной. Пусть l будет указывать на первый символ перед именем переменной, r — на первый символ после имени. Дальше:Теперь осталось вывести первую строку до символа номер l, затем новое имя, затем первую строку от символа с номером r и до конца.
А можете код показать?
F — динамика. dp[len][sum] — лучший ответ, который мы можем получить, если совершили len бросков и получили сумму sum. В каждой позиции два варианта, либо закончить, либо бросить ещё раз и перейти к следующему шагу, таким образом dp[len][sum] = max(sum/len, сумма dp[len+1][sum+i]/M (i от 1 до M)))
Как ты считаешь динамику? Начиная с последнего элемента что ли?
Да, сначала заполняешь для dp[n][sum] = sum/len, затем прогоняешь len от n-1 до 0 и в итоге нужно что-то вроде dp[0][0] вывести.
Сложность O(N^2*M)?
Кажется O(N*M), если не изменяет память. Чтобы взять сумму нескольких элементов массива, нужно вроде бы просто частичные суммы посчитать :)
По памяти, видимо, O(M), так как достаточно хранить всего один столбец, чтобы посчитать новый.
Сумма может быть до N*M, так что видимо в столбце O(N*M) элементов. Тогда и сложность O(N^2*M)
Да, извиняюсь, это правда, память всё-таки изменила мне :)
Блин, я так и не смог понять эту динамику.
Например, как заполнять таблицу для i = 0? Можно посмотреть код (кусок с динамикой)?
Код показать не могу, к сожалению, не знаю, как его найти, так как писал не на своем компьютере, но могу попробовать подробнее объяснить её суть: dp[len][sum] — мат. ожидание искомого выигрыша, при условии, что уже совершено len бросков, текущая сумма sum. Для каждого len и sum, кроме тех, где len = 0 или len = n, вариантов перехода у нас 2 — остановиться и забрать приз в размере sum/len или продолжать бросать кубик дальше. Понятно, что при len = 0 остановиться нельзя, так как мы еще не сделали ни одного броска, а при len = n бросать дальше нельзя, нужно обязательно забирать приз sum/n. То есть для 0 < len < n, dp[len][sum] = max(sum/len(что соответствует тому, что мы не будем продолжать игру), (dp[len+1][sum+1]+...+d[len+1][sum+M])/M(что соотвествует продолжению игры, формула именно такая, так как если мы бросим кубик ещё раз, то равновероятно получим одно из тех состояний, что записано в сумме, а такое суммирование возможно, наверное, в силу какого-нибудь свойства типа линейности мат. ожиданий))
Соответственно, для len = 0 dp[0][0] = (dp[1][1] + ... + dp[1][M])/M. Для len = n, dp[n][sum] = sum/n;
Надеюсь, что теперь стало понятнее.
Вот, http://pastebin.com/1EGP4nQj. Однако пришлось немного попихать по времени.
Сдавали в даблах? У нас WA26 все время был.
Проблем с точностью тут не может быть, т.к. при переходе к следующему слою динамики ошибка уменьшается в M раз. Ищите багу, 26 тест небольшой :)
Как решалась I?
Перебор левой границы + 2 указателя.
Какой левой границы?
Левая граница — начало наибольшей непрерывной последовательности выходных.
А два указателя зачем?
Чтобы найти правую границу. Слышал, что можно было просто перебрать правую границу, но я не додумался.
мы в тупую перебирали ответ(количество подряд идущих выходных,идущих подряд) и день, с которого эти выходные начинаются
мы тоже так делали, но почему то не зашло.
а как вы раскидывали оставшиеся выходные дни?
Жадно,с 1 января до начала праздников непрерывных и после их окончания до конца года. При этом всем учитываешь что какие то дни уже праздники и считаешь сколько для текущего ответа и позиции ты потратил выходных.
код в студию!
Код конечно не изящен и написан максимально тупо=)
Я решал такой динамикой: параметры — количество дней всего, количество выходных среди них, количество идущих подряд рабочих/выходных в конце, значение — ответ задачи. Преимущество — не надо думать, как распихивать оставшиеся выходные дни.
Другой вариант: бинпоиск по ответу, внутри перебор стартового символа, начиная с которого идёт искомая последовательность выходных, внутри проверка жадно за линию.
Итого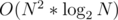 , где N — число дней в году
, где N — число дней в году
Как решать J?
div 1 или div 2?
Во втором диве — аккуратный квадрат. В первом — наверное FFT.
Что такое FFT?
Fast Fourier Transform. Быстрое преобразование Фурье.
А в первом диве задача так и решалась, подтверждаю.
Мы писали быстрое преобразование Фурье. Пусть наше число a0a1...an - 1. Тогда ответ равен сумме всех попарных произведений цифр aiaj, умноженных на некоторые степени десятки. А именно, aiai + k умножается на 10n - 1 - k. Нужно быстро уметь считать сумму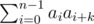 . Это можно сделать, перемножив два многочлена с коэффициентами (a0, a1, ..., an - 1, a0, a1, ..., an - 1) и (an - 1, ..., a1, a0) и внимательно изучив коэффициенты получившегося произведения.
. Это можно сделать, перемножив два многочлена с коэффициентами (a0, a1, ..., an - 1, a0, a1, ..., an - 1) и (an - 1, ..., a1, a0) и внимательно изучив коэффициенты получившегося произведения.
В дорешке Фурье пришлось запихивать, даже оптимизированная версия долго падала на разных тестах (видимо, было ТЛ +- эпсилон). Его как-то по-хитрому писали? Или просто во время контеста серваки мощнее стояли?
Долго пытался побороть H на контесте, но упорно получал WA 39.
Расскажите, пожалуйста, как её решать.
Мы тоже на это напоролись. Внутри пути могут быть одинаковые числа — при их наличии нужно отдельно вывести "No".
Переберем пары путей, составим граф. Очевидно, если в каком-то графе будет цикл, то построить нельзя.
В первом тесте из условия тоже был цикл. Надо было нарисовать.
Нужно было составлять граф по парам путей, а не по всем трем.
Ааа, тогда да. Не доперли до этого, фигачили по всем трем. Я снизу написал, как мы сделали, и я теперь понимаю, почему это верно.
Решаем отдельно для каждой пары путей. Найдем общие элементы в двух массивах. Теперь переберем эти общие элементы и для каждого из них (назовем его x) посмотрим в каждом массиве на его соседей. Пусть в первом массиве у элемента x есть сосед y. Тогда, если y содержится во втором массиве, но не является в нем соседом элемента x, то ответ No, т.к. кратчайший пусть из x в y достигается путем прохода по ребру между ними, что показано в первом массиве — но во втором пути между ними есть еще какие-то вершины.
Если все эти проверки завершились успешно — ответ Yes.
Дополнительное упражнение — решить (и доказать!) эту задачу для N путей.
Моё решение работает для N путей, но N должно быть небольшим.
А какие ограничения на N ты предполагал?
Работать-то может и работает, а вы докажите. Для 3х путей доказательство тупое, т.к. можно просто все случаи разобрать и графы предъявить. Для произвольного N поинтереснее.
Для 3х путей утверждение, что любая ошибка в паре, выглядит таким очевидным, что даже не хочется его доказывать, ибо проще получить Accepted)
Эх, моя ошибка, надо было в случае "Yes" попросить предъявить граф :)
Пример приводился очевидно — ищем "треугольник" этих трех путей в графе, вне его все без разницы, а веса вдоль него надо расставить так, чтобы для любой пары "сторон" выполнялось строгое неравенство треугольника.
Ну так я и говорю, что для 3х это просто. Но если "даже не хочется доказывать" — то почему бы не заставить участников немного подумать.
Ooooops, EPIC FAIL here.
Не понял примера. "1 2 3" и "3 4 1" противоречивы.
Ай ай ай, этот пример изначально неверен.
Я утверждаю, что решение, описанное ниже, будет работать для N > 3. В строгих доказательствах я не силён, поэтому буду рад увидеть контрпример.
Вообще моё решение — это не разбор пар путей.
Сначала для каждого пути я запоминаю вершину, с которой он начинается. Для каждой вершины я храню, в какие пути она входит + отдельно отсекаю случай, когда вершина дважды входит в один путь. Каждый путь — это отдельный граф.
Из начала каждого пути я запускаю dfs, в который передаю текущую вершину int v, вершину-предка int p, путь, по которому я иду int tp, и vector < int > last. В last[i] я храню последнюю просмотренную вершину, которая относится и к текущему пути, и к пути i. Если ещё не было ни одной такой вершины, то last[i] = - 1.
Каркас решения: запускается dfs по всем путям, если он не находит ничего плохого — ответ Yes. Таким образом, получается N dfs'ов, перед вызовом каждого я инициализирую last: все last[i] = - 1. Изначально предок = -1.
Подробно опишу сам dfs.
Вот и всё. Если мы прошли все dfs'ы без приключений и косяков, то выводим Yes.
Если что-то в решении непонятно — я готов пояснить. Могу показать код.
Казалось бы, вы просто проверяете для каждого пути, не противоречит ли он любому из остальных, пачкой, а не по одному. А по сути это то же решение.
Собственно, посмотреть, как вы это будете доказывать, гораздо интереснее :) Если для 3х путей ещё можно поверить в "интуитивную очевидность", то для N — уже сложнее (см. I_love_natalia, который пытался привести контрпример). Если так пугает слово "доказательство" — можете считать, что в задаче просят предъявить пример графа в случае "Yes" :)
Я понял, что утверждение, которое я пытаюсь опровергнуть, похоже, верно. По крайней мере, совершенно неясно, в чем может заключаться проблема, если в тривиальных случаях ее нигде нет.
А почему в качестве примера графа не подойдёт то, что нам дают в input?
Подойдёт, конечно, если веса правильно расставить.
Для N путей используем тот же алгоритм: перебираем пары путей, по ним составляем граф, в нем ищем цикл. Если цикл есть — ответ No, иначе ответ Yes.
Построим граф G = граф, составленных из всех путей.
Рассмотрим 2 случая: 1) Расставить веса возможно. Но тогда для каждой пары вершин будет существовать единственный кратчайший путь в G. Тоже самое верно будет и для графов Gij, составленных из путей i и j (они будут просто подграфами G и для них это автоматически выполняется).
2) Расставить веса невозможно. Но это означает, что будут существовать 2 такие вершины в графе G, для которых будет существовать 2 различных кратчайших пути. Покажем, что будут существовать 2 вершины, для которых эти 2 пути будут подпутями изначальных путей i и j.
Пусть 2 вершины a и b соединены кратчайшими путями c=c1...cn и d=d1..dm. Введем операцию T(a, b) = (a', b') — найдем такие вершины a' и b' принадлежащие двум кратчайшим путям c, d, что между ними есть 2 кратчайших пути. Если операцию T применить нельзя — получаем, что c, d являются подпутями каких-то из изначальных путей и мы получили цикл в графе Gij. Иначе возьмем в качестве (a, b) T(a, b) и снова повторим наши действия.
Почему вы не будете повторять эту операцию вечно, гуляя по циклу?
Да, точно :) Эту операцию применяем таким образом, чтобы либо длина пути c уменьшилась, либо длина пути d. Если мы не можем этого сделать, то значит эти 2 пути не пересекаются => противоречие (мы можем расставить числа так, что они не будут кратчайшими).
Хз, как мы сдали, но... Дикий рандом в общем. Закидывали все ребра в set. Потом в другой set закидывали вершины. Чтобы одинаковые уходили в общем. Потом сравнивали размеры set'ов. Если ребер больше, чем вершин, то "NO", иначе "YES". Вообще сначала была идея проверить на ацикличность, чтобы не было нескольких коротких путей(т.е. количесво ребер не более, чем количество вершин — 1, точнее равно), но на тестах из условия не работало. Но! Мы заметили, что если не вычитать единичку, то все работает. Отправили. И... Сдалось. Сидел с круглыми от удивления глазами. Пока не смог доказать, почему верно то, как мы решили. Если кто может объяснить, то объясните :) UPD. Понял
у кого-нибудь был ва9 в I?
Может кто-нить объяснить условие в G? Потому что наивное решение за N*K*log(N) у меня получает WA3, я просто пытаюсь отследить распространение ошибки после данного времени закидыванием в SET имен веток, которые сливаются или получаются в результате ответвления.
Пытался в дорешку сдать C (Cdecl), но получаю вердикт "Ошибка проверяющей системы". Куда писать об этом?