Прежде чем опубликовать разбор задач сегодняшнего раунда, приношу извинения администрации и участникам за свою глупую ошибку, допущенную по криворукости и неопытности.
Несмотря на то что раунд откровенно не удался, мы, авторы, рады, что многим участникам задачи понравились. Вот, собственно, решения:
A — Вася и автобусы
Во-первых, если n = 0, то ни одного ребенка по условию нельзя провезти. Значит, если при этом m = 0, от ответ (0, 0), иначе ответ Impossible.
Теперь n > 0. Если m = 0, то ответ, очевидно, (n, n). Иначе, чем больше родителей везет с собой по ребенку, тем меньше плата за проезд. Поэтому максимальная плата будет тогда, когда всех детей везет один родитель — получаем ответ n + m - 1. Если n < = m, то все n родителей везут детей, и ровно n детей не платят за проезд. Если же n > m, то все m детей распределяются по родителям и не платят за проезд. В обоих случаях получаем минимальный ответ max(n, m).
B — Окружение
Найдем минимальное расстояние между окружностями L. Тогда ответ к задаче равен L / 2.
- Пусть окружности лежат вне друг друга. Покажем, что L = d - R - r. Во-первых, ясно, что он достигается. Проведем отрезок соединяющий центры. Его часть, лежащая между точками пересечения с окружностями как раз имеет такую длину.










 Докажем, что меньшее расстояние недостижимо, построим отрезок между двумя окружностями. Тогда R + r + L > = d, откуда
Докажем, что меньшее расстояние недостижимо, построим отрезок между двумя окружностями. Тогда R + r + L > = d, откуда 


 L > = d - R - r, чтд.
L > = d - R - r, чтд.





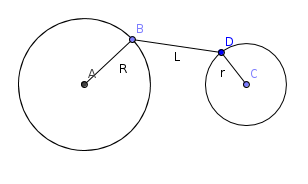
- Для окружностей, лежащих внутри друг друга аналогичными рассуждениями получаем L = R - d - r, где R — радиус наружной окружности, r — внутренней.
- Для пересекающихся окружностей ответ 0.
C — STL
Пусть нам дан массив строк (s1, s2, ...sn), где si = pair либо int.
Рассмотрим числа bali = разность количества pair и int на отрезке массива от 1 до i. Тогда утверждается, что восстановить тип по данному массиву строк можно, причем однозначно < = > bali > = 0 при 1 < = i < n и baln = - 1. Здесь возникает очевидная аналогия с правильными скобочными последовательностями.
Докажем это утверждение по индукции по количеству int в данном массиве. База для n = 1 очевидна. Пусть у нас есть тип pair < type1, type2 > . Тогда baln = 1 + balntype1+balntype2 = - 1. Также можем получить, что bali > = 0 для 1 < = i < n.
Пусть теперь у нас есть массив строк s, и в нем выполняется данное утверждение. Тогда первый элемент в нем — pair. Возьмем наименьшее i, что bali = 0 — оно существует по соображениям дискретной непрерывности (и не равно n, ибо baln = - 1) — в этой позиции должен заканчиваться type1. Тогда на отрезке [2, i] (для него несложно проверить предположение индукции) можно расставить знаки препинания, чтобы получился тип. Аналогичное верно и для отрезка [i + 1, n]. Значит, и из всего отрезка [1, n] можно составить тип, причем тоже единственным образом.
Теперь, если мы получили, что из данного массива строк можно составить тип, заведем функцию gettype(i), которая будет строить тип, начинающийся в si, и возвращать индекс, следующий после того, в котором она завершила построение. Как она будет работать? Пусть сейчас запущена gettype(i). Если si = pair, выведем int и вернем i + 1. Иначе выведем "pair < ", запустим gettype(i + 1) — пусть он вернул нам j. Выведем ", " и запустим gettype(j), он вернул нам k, выведем " > " и вернем k. Итого, запустив gettype(0), мы построим и выведем восстановленный тип.
Можно обойтись без предварительной проверки, можно ли составить тип из данного массива. Для этого можно запустить функцию gettype и, если в ходе построения типа получаются противоречия, выводить "Error occurred".
Асимптотическая сложность решения — O(количества данных строк).
D — Несекретный шифр
Решение riadwaw: Воспользуемся методом двух указателей. Будем поддерживать для каждого элемента, сколько раз он встречается на текущем отрезке [l, r]. При фиксированном l будем увеличивать r, если элемент a[r] встречается k раз, то этот отрезок и все отрезки вида [l, t], t > r нужно добавить в ответ и увеличить l. Чтобы поддерживать кол-во элементов нужно либо сжать координаты, либо воспользоваться структурой map. Также нужно не забыть, что ответ может достигать n * (n + 1) / 2, т.е не влазить в int.
Решение Kostroma: для начала сожмем координаты, аналогично первому решению. Выпишем для каждого числа список позиций, в которых оно встречается в нашем массиве. Теперь создадим массив b, в bi будем хранить номер позиции, в которой стоит число ai, при этом на отрезке [i, bi] число ai встречается ровно k раз (если такой позиции нет, то bi = n + 1). Это несложно сделать одним проходом по нашим спискам. Найдем, сколько отрезков с началом в i удовлетворяют условию задачи — для этого из n нужно вычесть такое минимальное j, что на отрезке [i, j] есть k одинаковых чисел (если такого отрезка нет, то j будем считать равным n + 1). Но такое минимальное j есть 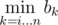 . Такие минимумы для всех i можно найти, пройдя массив a один раз с конца. Осталось только просуммировать ответы для всех i от 1 до n.
. Такие минимумы для всех i можно найти, пройдя массив a один раз с конца. Осталось только просуммировать ответы для всех i от 1 до n.
E — Контратака
У этой задачи много различных решений. Для начала, конечно же, сопоставим городам вершины графа, а дорогам — ребра. Теперь нам нужно найти все компоненты связности в дополнении данного графа.
Решение Gerald: будем хранить set a вершин, которые еще не были посещены, и запустим серию обходов в глубину. Предварительно отсортируем списки смежности каждой вершины — теперь мы можем за O(logn) проверять, есть ли в данном графе произвольное ребро. Пусть мы сейчас находимся в вершине v. Пройдемся по всем элементам a, пусть мы сейчас рассматриваем вершину 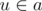 . Если ребра (v, u) нет в данном графе, то в его дополнении оно есть = > выкинем из a вершину u и добавим ее в очередь. Иначе ничего с вершиной u не делаем. Сколько же раз с вершиной u будет повторена такая операция? Заметим, что вершина u остается в set-е только тогда, когда в данном графе есть ребро (u, v), то есть не больше раз, чем степень вершины u. Значит, асимпотика такого решения равна O(M * logn). Логарифм появляется из бинарного поиска. Это решение без каких бы то ни было оптимизаций тратит чуть больше 2 секунд. Если использовать хеш-таблицы, чтобы узнавать, есть ли в графе определенное ребро, получим асимптотику O(m).
. Если ребра (v, u) нет в данном графе, то в его дополнении оно есть = > выкинем из a вершину u и добавим ее в очередь. Иначе ничего с вершиной u не делаем. Сколько же раз с вершиной u будет повторена такая операция? Заметим, что вершина u остается в set-е только тогда, когда в данном графе есть ребро (u, v), то есть не больше раз, чем степень вершины u. Значит, асимпотика такого решения равна O(M * logn). Логарифм появляется из бинарного поиска. Это решение без каких бы то ни было оптимизаций тратит чуть больше 2 секунд. Если использовать хеш-таблицы, чтобы узнавать, есть ли в графе определенное ребро, получим асимптотику O(m).
Решение Kostroma: Рассмотрим компоненты дополнения нашего графа. Рассмотрим такой набор компонент дополнения, что их суммарный размер не больше n / 2 и наиболее близок к n / 2 (если такого набора не существует, то в дополнении одна компонента) — пусть в них в сумме c вершин — назовем это множество A. Тогда все ребра между этими с вершинами и остальными n - c вершинами должны быть в данном графе, то есть c·(n - c) < = m. Отсюда получаем, что 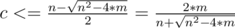 . Если n2 < = 4·m, то n < = 2·103, тогда c < = 103. Иначе при фиксированном m для роста оценки на c нужно уменьшать n — вплоть до того, пока не выполнится n2 = 4·m. Тогда
. Если n2 < = 4·m, то n < = 2·103, тогда c < = 103. Иначе при фиксированном m для роста оценки на c нужно уменьшать n — вплоть до того, пока не выполнится n2 = 4·m. Тогда 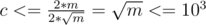 . Значит, мы получили, что c < = 103.
. Значит, мы получили, что c < = 103.
Рассмотрим теперь любую другую компоненту, пусть в ней b вершин. Тогда c + b > = n - c, так как c + b > n / 2 в силу выбора множества A, а значит, если c + b < n - c, то можно взять множество компонент, в которое входят все компоненты, кроме A и еще одной компоненты из b вершин — в нем n - c - b вершин, и c < n - c - b, n - c - b < = n / 2. Значит, если в дополнении больше одной компоненты, то есть компонента размеров не меньше чем n - 2·c (назовем ее большой), значит, во всех остальных компонентах в сумме не больше чем 2·c вершин (причем в A ровно c вершин, значит во всех компонентах, кроме большой, не больше чем c вершин). Тогда не лежать в большой компоненте могут только вершины, степень которых в исходном графе как минимум n - c. Значит, все вершины со степенью < n - c лежат в одной компоненте, а значит, все вершины со степенью < n - 1000 тем более лежат в одной компоненте. Множество этих вершин назовем B. Построим новый граф из вершин, не принадлежащих множеству B и еще одной вершины: для каждой пары вершин не из B ребро будет проведено тогда и только тогда, когда в исходном графе его не было. Сопоставим множеству B вершину D, тогда ребра между D и произвольной вершиной v не будет тогда и только тогда, когда в исходном графе v соединена со всеми вершинами из B.
Сколько же в новом графе будет вершин? Количество вершин, степень которых в данном графе как минимум n - 1000, и еще вершина D, то есть не больше чем 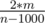 + 1 =
+ 1 = 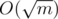 . Значит, ребер в графе будет O(m). Теперь запустим серию обходов в глубину или ширину на таком графе и найдем в нем компоненты связности. Теперь нетрудно восстановить компоненты связности дополнения: для этого нужно лишь вспомнить, какие вершины попали в множество B. Получаем решение за O(m), работающее чуть меньше секунды.
. Значит, ребер в графе будет O(m). Теперь запустим серию обходов в глубину или ширину на таком графе и найдем в нем компоненты связности. Теперь нетрудно восстановить компоненты связности дополнения: для этого нужно лишь вспомнить, какие вершины попали в множество B. Получаем решение за O(m), работающее чуть меньше секунды.
Решение riadwaw:
- Посчитаем степень каждой вершины в исходном графе, выберем вершину с минимальной степенью — назовем её V. O(m)
- Заметим, что ее степень не больше средней степени вершин, т.е 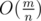 .
.
- Заметим, что все вершины, кроме соединенных с V в исходном графе, будут лежать в дополнении в той же компоненте связности, что и V — назовем это множество вершин A.
- Таким образом, можно явно построить дополнение графа, содержащего V и все вершины, соединенные с ней. Всего ребер там 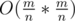
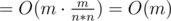 , так как m < n·n. Переберем все эти ребра, объединим с помощью СНМ соединенные вершины. Кроме того, объединим с компонентой, содержащей V, вершины, которые в исходном графе соединены не со всеми вершинами из A.
, так как m < n·n. Переберем все эти ребра, объединим с помощью СНМ соединенные вершины. Кроме того, объединим с компонентой, содержащей V, вершины, которые в исходном графе соединены не со всеми вершинами из A.
В асимптотике могут вылезать лишние логарифмы из СНМ или сжатия координат. Общая асимптотика от O(m) до O(mlogn), решение работает около секунды.











Стоп:) Контест через 3 часа:)
Печалька :-(
Если одна окружность внутри другой, то разве ответ не 0?
Нет, мы должны нашим кругом (радиуса ноль) задеть окружности.
Ну так воины будут бежать к центру и все равно его заденут. Или я что-то не так понял?
нужно зафиксировать радаром именно начало движения войск
fail
In description of B propably is a typo: "one circle is into another" appears for two of three cases
thank you, fixed now
Контест хоть и провалился, но сами задачи и разбор великолепные! Ребят, спасибо за труды!
мэп в Д разве заходит?
А почему нет?
вот такое заходит по крайней мере.
На самом деле в B два вложенных тернарных поиска, а внутри еще бинарный. Наверное
Кто как извращается.
а как внутри бинарным? я только тернарным умею...
за O(logn) проверять, есть ли в данном графе произвольное ребро
а почему не сделать это через хэш-таблицы за O(1) ?
можно и так.
I think that the limits of problem C are a little bit strict, My solution got TLE on case 8 and it goes like this: - create a stack of string - loop over the tokens from the end to the beginning - step 1: if it is a token "int" then add it to the stack - otherwise - step 2: as it is a token "pair" then take the last two elements s1 and s2 ,remove them from the stack and then push into the stack the following string s = "pair<" + s1 + "," + s2 + ">" - in case that in step 2 there are not two strings to take from the stack or the stack doesn't contain exactly 1 element at the end of the process then the input string is invalid. My algorithm failed because the concatenation is really costly. I could have made it better but that is what I first thought at contest.
Concatenation is O(N), so your overall solution would have O(N^2) complexity. I don't think adding a couple of seconds to the time limit is going to fix that.
Решая задачу E на Java внезапно обнаружил, что операция
set.clear(), гдеset = new HashSet<Integer> ();, даже если set не содержит элементов работает очень долго. Это на будущее Java-кодерам.Это почти на все коллекции распространяется, кстати: ArrayList, PriorityQueue. Только TreeSet нормальный.
Странно, решение D с map заходит. Но решение c multiset TL на 14 тесте. Разница только в структуре. Может кто-нибудь знает, что такого в multiset, что он так тормозит? код с multiset
http://www.codeforces.ru/blog/entry/4408#comment-89785
Напишу свой вариант решения С, возможно, кому-то он покажется проще. Введем понятие баланса
b. Его смысл таков: это неотрицательное число, которое показывает, сколько еще "типов" надо дописать к имеющейся строке, чтобы получить "правильную". Например, для строкиs="pair", b=2, а дляs="pair int int", b=0. Считатьbдостаточно просто: если первый тип в заданной строке — "pair", тоb=2, а если "int", тоb=0. Далее идем по массиву строк (который мы получили в результате сплита заданной строки по пробелу) и если встречаем "pair" — увеличиваем на единицуb(потому что для только что прочитанного типа "pair" нужно еще 2 закрывающих типа, однако он сам является одновременно закрывающим типом), а если встречаем "int" — уменьшаем на единицу. Заметим, что если изначально выбратьb=1, то никакой дополнительной логики обработки первого элемента в массиве писать не потребуется. Далее заметим, что если в какой-то моментb==0, возможны 2 варианта: а) мы читали последний элемент массива, тогда решение существует; б) мы читали какой-то другой элемент, решений нет. Очевидно, что если так и не было полученоb==0, то решений также нет. Получить само решение теперь достаточно просто. Напишем метод, который идет по массиву строк и добавляет к результату или "int", или "pair" с рекурсивными вызовами себя и некоторым форматированием. В коде это выглядит так:Полный код этой идеи: 1702285
В моем решении небыло никакого баланса, функция очень похожа на твою, только вначале стоит проверка что pos не вылезет за границу массива, иначе ответ Error, после вызова функции в main проверяем что pos указывает на последний элемент массива, иначе опять Error. Всё. Никаких балансов и извратов с разностями чего-бы то ни было.
У меня похожее решение, только на Java (1705957), не заходит по TL.
Используйте StringBuilder а не String для результирующей строки.
Зашло, спасибо. Понадеялся на JIT, ибо обычно простая конкатенацию в цикле представляет собой StringBuilder в байт-коде. Видимо, конкатенации в рекурсивных вызовах распознавать пока что он не умеет.
Никакой JIT тут не поможет — StringBuilder в байт-коде каждый раз создается заново.
Вот это:
превратится после компиляции примерно в:
Ночь, улица, фонарь, аптека.
Бессмысленный зеленый цвет.
Пиши еще хоть четверть века -
Все будет так. Исхода нет.
Сольешь — начнешь опять сначала,
И повторится все, как встарь.
String, плюс-равно, TL на Java,
Аптека, улица, фонарь.
в разборе как бы то же самое :))
I don't understand the complexity analysis for the 2nd solution for problem E. Each vertex u remains in a no more than it's degree, but it's degree could be m right? So isn't the complexity then O(m^2 logn) ?
Degree of one vertex can be m, but sum of all degrees for all vertexes is 2 * m.
would u please explain what does DSU mean?
Disjoint-set union (or disjoint-set data structure)
thank you
Может кто-то пошагово рассказать, как делать Е? Первым способом я не могу уложиться в ТЛ (если я его правильно понимаю, пишу на C#), второй и третий понимаю не очень.
Объясню второй способ более на пальцах, без горы формул. Рассмотрим макс тест N=10^5 вершин и E=10^6 рёбер в инпуте. Предположим у нас есть две компоненты связности размера A и B A+B=N. Раз это разные компоненты связности все рёбра между этими двумя множествами вершин должны быть заданы в инпуте, чтобы они были несвязаны между собой в инвертированном графе. Раз так, то A * B <= E. т.е. либо A <= sqrt(E) либо B <= sqrt(E) (sqrt(E)=1000). Соображения в этом направлении более детально расписанные во втором решении от Kostroma, позволяют сделать вывод, что у нас есть не более одной компоненты связности в которой более 1000 вершин, назовём множество вершин этой компоненты "Big". В остальных компонентах вместе взятых вершин не более 1000. Но т.к. дороги двусторонние, венера в зените, а меркурий убывает, на самом деле везде в тексте выше 1000 нужно заменить на 2000 (подробнее смотри решение Kostroma) Поняв это теперь достаточно определить какие вершины принадлежат множеству Big, ему принадлежат все вершины со степенью меншьей чем n — 2000(в том графе что дан в инпуте). т.к. в инвертнутом графе у этой вершины будет более 2000 соседей, а это воможно только для одной компоненты которую мы обозвали Big. Для остальных ~2000 вершин можно построить граф в явном виде и DFSом найти компоненты связности.
3 — ий способ, самый лёгкий и понятный для меня:
DSU если не знаешь, там ничего сложного.
С помощью него будем объединять вершины в множества.
1. Как и сказано, находим вершину с минимальной степенью — V
2. Сортируем её список смежности
3. Объединяем со всеми вершинами, не соединёнными с V:
5, С этими вершинами мы уже закончили, осталось максимум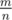 вершин, для них также как в пункте 3 строим явно граф и ищем компоненты связности в нём (добавляются рёбра только из тех вершин u, у которых get_set(u) != V и рёбра из V)
вершин, для них также как в пункте 3 строим явно граф и ищем компоненты связности в нём (добавляются рёбра только из тех вершин u, у которых get_set(u) != V и рёбра из V)
Тыц
Спасибо, с этим вариантом разобрался, с самого начала дело было в моем способе чтения чисел, у меня есть только методы Read(int bytes) и ReadLine(), я читал целую строку и потом ее парсил, теперь читаю посимвольно и делаю что-то вроде
x *= 10; x += t - '0';, однако этот способ все равно работает очень долго (у меня 2900+ мс после некоторых оптимизаций, напомню, что пишу на C#). Самое адекватное, что я пока могу придумать — 1714165, здесь я храню 2 списка вершин — на текущем шаге и на следующем, в каждой итерации БФСа я перебираю все вершины текущего списка и или использую их, или добавляю в список для следующего шага. Так что я все еще ищу хороший способ с запасом по времени. Странно также то, что как-то очень медленно работают хешсеты, в своем решении я храню список вершин в массиве (List<int>), сортирую его и затем ищу в нем элементы бинарным поиском. Если я используюHashSet<int>, который согласно документации обеспечивает проверку наличия элемента за O(1), то получаю ТЛЕ. Кто-то из пишущих на C# с таким сталкивался?много хешсетов будут работать скорее всего долго, ибо будет много раз вызываться стандартный конструктор
кстати, могут знающие люди сказать, сколько памяти занимает пустой хешсет, например, на C++ (unordered_set)?
Да, много хешсетов с несколькими элементами действительно работают медленно. Зато можно хранить все ребра в одном
HashSet<Int64>, например так: для каждого ребра ребра (u,v) добавляем в сет500000*u + vи500000*v + u. Тогда работает значительно лучше (2440мс): 1719412Дай код глянуть.
**Upd:** У меня был ТЛ на C++ из-за чтения данных, все таки 2 млн интов считать
cinом это довольно долго, со scanf зашлоI have a problem with task E. I am writing in Java and I get TLE on test 12. Here is my code http://codeforces.net/contest/190/submission/10214647 . There are only 3-4 accepted Java codes, but they used BFS soluton with binary search insted of DSU. I am using hashset instead of list with binary search, so it should run faster. How can I improve this ?
My solution
Problem E can be also solved using binary indexed trees. My solution runs in
O(m+n log^2 n), but this idea can be reduced toO(m+n log n).Can you plz share your approach?
i'm getting tle at problemE:Counter Attack on test case 12. Here is my code. Do you suggest any improvement? I'm using the 2nd approach explained at the editorial.
The C problem can be done by maintaining a stack. Maintain a brace_count array and a comma array of size as large as the input, they will tell us the number of end braces and comma required in the answer string. As you're reading the input: 1.) if the input is a pair push 0 into the stack. 2.) if the input is an int: i.) if the top is 0 make it 1, and put comma[i]=1. ii.) if the top is 1 a.) make brace_count[i]++ (for putting the as the pair is completed now b.) keep popping until the top becomes 0 and then go to a.) again. if the stack is non-empty or it becomes empty during the reading process, then there is an error. For printing the answer: 1.) start printing from the input, if comma[i]==1 print a comma after it,if the brace_count[i] is not 0 start printing the endbraces between input and comma. if there is a pair in input put an opening brace after it
Hint on problem E: As N getting bigger but M is limited at 1e6, there will always be a dominant component. Using dsu and start at the vertex with smallest reverse degree for that big component and bruteforce on those vertices with biggest reverse degree for smaller component.