Блог пользователя Petr

Power towers problem
Автор Petr, 13 лет назад, По-английски

I've talked about a problem from today's dress rehearsal in http://petr-mitrichev.blogspot.com/2012/05/world-finals-day-2-upe-dinner.html

Here's the first tough testcase for it: http://petr-mitrichev.blogspot.com/2012/05/power-towers-problem-testcase.html

Good luck! :)

  • Проголосовать: нравится
  • +20
  • Проголосовать: не нравится

»
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

You say you have a solution. Can you give an idea?

→ Ответить
»
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

And towers to compare can be of different height?

→ Ответить
  • »
    »
    13 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится

    I don't see a reason for them not to be. Anyway, you can add some ^1^1^1... to the end.

    → Ответить
»
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

It seems that the same problem is discussed here.

There is written:

Then

A1 < B1
is equivalent to
and:

But what does

mean?

→ Ответить
  • »
    »
    13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Apply the function n times

    → Ответить
    • »
      »
      »
      13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      Then you can get negative number that seems strange.

      → Ответить
      • »
        »
        »
        »
        13 лет назад, # ^ |
          Проголосовать: нравится +13 Проголосовать: не нравится

        Yes you are right, I may be wrong but I think there's an error with the formula above. It only has the first step done, but it doesn't hold for the next

        log(log( A_2 x log( a_1))) = log( log(A_2) + log(log(a_1)) )

        And then you have a sum which you cant get rid of because you can't distribute the next log

        → Ответить
      • »
        »
        »
        »
        13 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится

        But, it depends on what you get as a base of logarithm, I think, take Natural Logarithm and since ln(x) increases when x>0, so if we get a negative number, the first number is less than the second one, but not sure still

        → Ответить
        • »
          »
          »
          »
          »
          13 лет назад, # ^ |
          ← Rev. 5   Проголосовать: нравится 0 Проголосовать: не нравится

          Obviously, logarithm's base does not have influence on that property.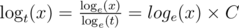
          P.S. Of course iff we have positive base, since .

          → Ответить
»
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

My unproved and probably wrong solution is like this. Let's evaluate the tower from top to bottom in floating point number until it's too large to go further. Then we discard the remaining bottom part of the tower and just compare the accumulated top values (if bottom parts are of equal height). Also, before doing all that, we have to somehow normalize the numbers and consider longest common top part.

→ Ответить
  • »
    »
    13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    I encourage you to implement it (it shouldn't be that big, should it?) and test it against the above testcase :)

    → Ответить
»
13 лет назад, # |
  Проголосовать: нравится +5 Проголосовать: не нравится

I saw a similar problem at the IFMO's Internet Olympiad (russian statements, problem G). Unfortunately, jury's solution and tests are incorrect.

→ Ответить
»
13 лет назад, # |
← Rev. 2   Проголосовать: нравится +8 Проголосовать: не нравится

The test case posted is easy in the sense that it can be solved with loglog

let a=54^8^35^4

let b=19^55^92^3

log log a = 35^4 * log(8) + log log 54 = 3120463.347019

log log b = 92^3 * log(55) + log log 19 = 3120463.343260

But I can't see a way to generalize this. Is it a correct way to approach the problem?

→ Ответить
  • »
    »
    13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    I think this method can't be generalized because of accuracy of calculations. But this must be analyzed, maybe it is enough to use "Big" floating numbers.

    → Ответить
»
13 лет назад, # |
  Проголосовать: нравится +13 Проголосовать: не нравится

still waiting for the solution.

→ Ответить
»
13 лет назад, # |
  Проголосовать: нравится -18 Проголосовать: не нравится

hmmm, seems like ITERATIVE LOG (log*) function should do the work, shouldn't it ?

→ Ответить
  • »
    »
    13 лет назад, # ^ |
      Проголосовать: нравится +5 Проголосовать: не нравится

    I think, that iterative log with checking for equality by using modular arithmetic solves this problem. But I can not prove that.

    You can denote precision problems like

    8^3^7^2
2^9^5^2
(equals)

    7^8^3^7^2
5^2^9^5^2
(the first is greater)

    2^6^99^99^99^99
99^5^99^99^99^99
(the first is greater)

    and so on.

    → Ответить
  • »
    »
    13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    You should have great precision problems implementing it in standart float pointer arithmetics. double precision is not more than 1018, and it's not enough (even for the testcase given by Petr in this post, I think).

    → Ответить
»
13 лет назад, # |
  Проголосовать: нравится +30 Проголосовать: не нравится

It seems that we need to find the maximum equal upper part of two towers, i.e. such minimal i and j that ai^ai + 1^...^an = bj^bj + 1^...^bm for towers of heights n and m. To find potential i and j level-index arithmetic (some sort of implementation of iterative log idea) can be used. Then the equality must be verified using some exact computations.

By the way, how does modular arithmetic help to solve the problem? In particular, it is not clear how to prove that two towers are equal. If we found that two towers are not congruent modulo p, where p is prime, then they are not equal. However, the converse is not always true.

There are several reasons to find equal part of towers. The first is that it seems to be the only way to pass some tests. For example, if a = 5^99^99^99^99 and b = 6^99^99^99^99, then lnlna = lnln5 + ln99 × 99^99^99 and lnlnb = lnln6 + ln99 × 99^99^99. So, these expressions differ only by last few digits. If you want to deal with approximate representations of numbers, then you will have to store all significant digits, which is absolutely impossible.

The second reason is that if two towers are not equal, then it is affected very much by upper powers. I mean that if we have upper part of the first tower sufficiently larger than of the second, then we can't make the whole first tower smaller by modifying its lower part. For example, build two towers of equal height: the first with 16 on its top and the second — with 2. The first tower will be always greater then the second under given conditions: a1^a2^...^an - 1^16 > b1^b2^...^bn - 1^2, where n ≥ 1 and 2 ≤ ai, bi ≤ 100 for 1 ≤ i ≤ n. This can be generalized:

This means that if the ratio of a and b is at least 10, then ratio of two towers, which have a and b on the top (bottom parts must have equal lengths), will also be at least 10 under constraints, given in the statement. So, if we process towers consequently from top to bottom, and at the same level found that first is sufficiently greater than the second (more than 10 times), then the whole first tower is greater.

One more important property is the following. If tops of two towers are big enough, but the second is slightly bigger, then the whole second tower will be at least 10 times larger then the second (here the previous property is taken into account).

This means that we will have to deal only with real numbers, bounded with something about 109, unless there exist pairs of different almost equal towers, greater than this bound, but I can't see any way to prove it, except testing on all such cases. The bound 10 - 8 is taken based on two Petr's tests and can be lowered if necessary.

Sorry for cumbersome post, there are only some ideas on how to solve the problem. They may lead to a solution, very similar to al13n's one, and show that his solution is very likely to be correct.

→ Ответить