Problem link: Light OJ 1392.
Please give it a read. If I understood correctly, given R, T, N, it asks to find number of pairs (r, t) with 0 ≤ r < R, 0 ≤ t < T such that there exists integers a1, ..., ar whose sum is t and each of the numbers ai is between 1 and N (inclusive). Constraints are 1 ≤ R ≤ 108, 1 ≤ T ≤ 4 * 108, 2 ≤ N ≤ 20.
But then for a fixed r, all t between r and Nr should be reachable (others are not reachable because each of the r variables is at least 1 and at most N). So I ran a brute force (to check), but they don't match the sample.
Code: here.
Interesting enough, the output of the brute force for each sample is exactly 26 more than actual answer. Where did I go wrong?











Ok, you assumed the situation the second team will be given, wouldn't have to abide by any rules. For example, the r = 2 and t = 1, is just not a valid situation because the team has to score at least one point per game. So saying that the team scored 1 point in 2 games doesn't make sense. So these situations can't be given to the second team. You are overcounting these situations. I wrote an actual and two brute solutions for this problem. But all of them give 1 more than the sample. I really don't know what is going wrong with my brute force. Can you check my brute force code and check for any mistake ? Brute Force code with comments
I've just got accepted in the problem. Apparently the setter's solution does not include the case Tint = T and Rint = R. So the correct constraint is 1 ≤ Tint < T and 1 ≤ Rint < R.
Thanks, Alpha_Q. I've got AC now. I had to take care of another thing to get AC though. The judge data contains cases where R < T and also cases where R > T*n. I assumed that Judge data will contain only valid situations for the first team. So my code was generating negative outputs for these cases. I had to check for these cases at the beginning and print 0 for them to get AC. Btw Alpha_Q, is your solution O(1) ? I solved it using
Squareroot decomposition. I also think I can solve it using Binary Search. But I don't have any O(1) idea.
Yes, my solution is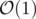 .
.
Notice that for a fixed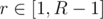 we need number of integers
we need number of integers 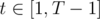 satisfying the conditions r ≤ t ≤ Nr, R - r ≤ T - t ≤ N(R - r).
satisfying the conditions r ≤ t ≤ Nr, R - r ≤ T - t ≤ N(R - r).
We can rewrite the second condition as Nr + T - NR ≤ t ≤ r + T - R, and combine with the first condition to get
So our answer is
$0$. Now notice that since N ≥ 2, the value Nr will eventually dominate r + T - R, and the value Nr + T - NR will eventually dominate r. We just need to find the point where one dominates the other. This is easy to do
So now
These can be calculated in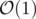 . Another detail is that we need to adjust values of low and high with our initial bound 1 ≤ r ≤ R - 1. My code.
. Another detail is that we need to adjust values of low and high with our initial bound 1 ≤ r ≤ R - 1. My code.