AtCoder Grand Contest 002 will be held on Sunday (time). The writer is sugim48.
Let's discuss problems after the contest.
UPD: Thank you for participation. Editorial (English at the bottom)
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
24:43:24
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
24:43:24
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 16:51:37 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Wow is writer of AGC002 sugim48?
It's a good news for us! We know that he is writer of TCO 2015 Semifinal 250pt and Final 600pt. Thus, AGC002 will be very interesting contest as well as AGC001!
I like sugim48's problems much. Unfortunately there are only two problems wrote by him in English while he have wrote many interesting problems in Japanese, so I'm very happy as his fan to hear that his problems will be used for a global contest.
I think that sugim48 is one of the most strong problem setter of japan! It has been decided that this contest is very nice contest!
Can you please make impossible to judge the solution if it doesn't pass the examples? I lost 5 minutes because i submited the unwanted solution.
Hello rng_58 ... Im new to your site. Will editorials be published for the problems of the Grand contest?
Yes please recheck my main post :)
Thank you..
Auto comment: topic has been updated by rng_58 (previous revision, new revision, compare).
I'm new on this site as well. Is there any way to see other contestants solutions or editorials? I am really curious how to solve the 5th problem (candy piles) I thought that it may be some invariant and did a brute force to observe patterns of the winning or losing states but I wasn't able to find a general rule. I really liked the set, especially the 6th one. Congrats for a very nice contest :)
LE: I see the editorial has been posted so I'll read the solution there
Here you go
Thanks
looks like running times of codes are fairly different on codeforces and atCoder, my O(Q*root(N)) got TLE in D :(
Hmm, maybe codeforces uses very fast server. Anyway you can test your code from "Custom Test" tab.
I did it in N * log2(N) and it passed in 1.5 seconds — let's build DSU tree, using binary lifting on it we can find for each vertex what will be the size of its component at moment T in log(N); it allows us to apply binary search for each query separately. Intended solution is both faster and simpler :(
@sugim48, thanks for this awesome problemset :)
I also have a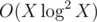
solution where X is say N + M + Q, and it also passes in a bit under 1.5 seconds. The solution is a bit different: it builds a partially persistent (no branching) DSU with size heuristic.
The first step is to construct the DSU. For each vertex, we maintain a growing array of records of the form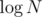
.
(parent, subtree-size, timestamp). When the program unites two connected components, it has to append two new records, one for each of the roots being connected. The size heuristic is there because we need the size anyway, and it guarantees that the depth of each vertex is at mostThe second step is to process the queries. Naturally, we do a binary search on the timestamp. Inside, we calculate size for the specific timestamp using the respective version of the DSU.
My first try was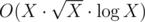
which timed out on like half the tests.
Edit: I've got to say the parallel binary search idea from the tutorial is just awesome!
My approach worked in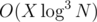
(I guess?) and it went really fast (~600ms), probably tests were bad or I don't know...
30 seconds after the contest ended :C
My solution worked like this:
We actually need to maintain all versions of DSU to do the binary search and solve task online, but we can keep something like
vector <pair <int, int> > parent[N]where we store pair (a, b) in parent[i] if in version a parent of i became b. Notice that after we build our DSU, this array will be sorted by version part of pair automatically.Now to find parent of some vertex X in version V we need to do binary search in
parent[X]to find two pairs (a1, b1) and (a2, b2) such that a1 ≤ V < a2, how much does getparent(x) operation last now?Notice that total memory usage is O(N) because on each union operation only one node gets new parent. So in total on the path from arbitrary node X to root of it's component:
So total running time of all binary searches in them is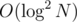
in total.
Unfortunately, this is O(log2), because if size[parent[v]] is equal to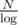
, then total running time of these binary searches is 
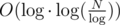which is equal to 
.
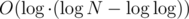But such test seems to be hard to construct though.
And depth of any node can be made O(log) by using rank or size heuristic, making getparent O(log2) time in total.
Hmm, by this argument, mine is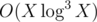
instead of 
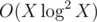too. Nice catch! I thought that the complexity of a single DSU operation somehow reduces to sum of logarithms instead of their product.
Indeed, I was able to use a ternary construction to make a test where my solution runs more than 2x slower.
my O(Q*root(N)) solution passed but after some optimization.
In the editorial, some of the diagrams for problem E are in the section for problem F.
Getting WA from test case 31 to 38 on problem 3.I am using 2 pointer approach .ANy idea?http://agc002.contest.atcoder.jp/submissions/826806
Try this
oops my approach is wrong.Thnks.I am very weak at provin correctness
In problem D ,For the approach in Editorial How can we compute number of reachable nodes for brothers in O(1) for any 1...i edges?
Store the size of each component in your DSU.
When adding edges to DSU you can maintain sizes of components as well — when merging two components, resulting component will have size equal to sum of sizes of old components.
Now when you need to check number for some brother at some moment t — just take a look at size of his component after adding t edges.
but in this way after adding each edge I would have to look at all brothers right?
Well, now your question sounds more like "how parallel binary search works". Try reading editorial once again ;)
The idea is — first you can figure out for which queries answer is at least M/2 and for which it is smaller. Now you just erase all your DSU and run second iteration; on second iteration for queries from first group you can find which of them have answer at least 3*M/4 and which have smaller answer, and for queries from second group you can find which of them have answer at least M/4 (and for which it is smaller). The trick is — on second iteration you can add M/4 edges, check everything you need here, after that add edges with indices M/4+1, ... , 3*M/4 and check everything for other group. You know which queries to check at moment M/4 and which queries to check at moment 3*M/4. By extending this idea from 2 iterations to log(N) iterations you'll get what editorial describes — maybe it isn't very detailed, that's true, so my "read editorial again" advice may be not very helpful :)
Now the editorial is a bit more detailed.
Awesome! Quite easy to understand now.
Awesome question quality and short problem description. To the point. Great going guys.
Wow！Ratings are updated just now.And semiexp become rank 1.Let's congratulate him!
Again, very nice tasks. Thanks!
D is the only one I feel a bit classic: I used this idea in LimitedMemorySeries1, and here is a task more similar.
My favorite one is C: it looks crazy at beginning, but the solution is quite simple.
Can you please explain the approach to solve this problem: LimitedMemorySeries1
http://codeforces.net/blog/entry/45578
One question. How can we see the test cases like we see in codeforces? This would be of great help to debug our code. I was wondering whats wrong in this greedy approach for C.
Yes, we know that will be very useful. We'll discuss if we can publish it in some way.
try test:
4 10
5 5 1 5
correct answer:
Possible
3 2 1
First of all, thanks for the awesome test case :D
So it means whenever end point is same, I will pick from the side that finally exposes me to the lower number. (5, 5, 5, 12, 6, 3, 5, 5) so 12 > 3 and hence I should pick up from the right hand side.
I solved my first problem using parallel binary search :D