Hello, Codeforces!
We are happy to announce that we're going to host a new contest at csacademy.com. Round #10 will take place on Saturday, Aug/06/2016 11:00 (UTC). If you want to take part in this round you need to register before the contest begins. Just like the previous rounds, this will be a Div1 + Div2, with 7 tasks of varied difficulty. We are honoured to have Yury_Bandarchuk as a problem setter.
This round is going to have some money prizes, as follows:
- First place: 125$
- Second place: 100$
- Third place: 75$
- Fourth and fifth place: 50$
- Two more special prizes, each consisting of 50$. The criteria for the special prizes is not chosen yet, but we will make it public after the contest.
Also many thanks to HellKitsune for translating the tasks in Russian.
Platform changes since Round #9:
- Added auto-complete to the editor
- Worked on cross-browser compatibility
- Added C# support
- Small UI improvements
Contest format:
- You will have to solve 7 tasks in 2 hours.
- There will be full feedback throughout the entire contest.
- Tasks will not have partial scoring, so you need to pass all test cases for a solution to count (ACM-ICPC-style).
- Tasks will have dynamic scores. According to the number of users that solve a problem the score will vary between 100 and 1000.
- Besides the score, each user will also get a penalty that is going to be used as a tie breaker.
About the penalty system:
- Computed using the following formula: the minute of the last accepted solution + the penalty for each solved task. The penalty for a solved task is equal to log2 (no_of_submissions) * 5.
- Solutions that don't compile or don't pass the example test cases are ignored.
- Once you solve a task you can still resubmit. All the following solutions will be ignored for both the score and the penalty.
We still recommend using an updated version of Google Chrome. If you find any bugs please email us at [email protected]
Don't forget to like us on Facebook, VK and follow us on Twitter.










You got the date wrong !
Fixed, thank you.
Any ideas about faster than O(NQ) solution for the last problem?
We can divide all queries to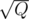 blocks. After each block we want to recalculate all the values in
blocks. After each block we want to recalculate all the values in  time. This can be done if we will do DFS with all active queries in a treap (sorted by y). When we go down we should take only those queries whose y is not greater than y of the edge. When we answer the query we should iterate over the current block and check if we should apply particular query. It can be done similar to finding LCA in
time. This can be done if we will do DFS with all active queries in a treap (sorted by y). When we go down we should take only those queries whose y is not greater than y of the edge. When we answer the query we should iterate over the current block and check if we should apply particular query. It can be done similar to finding LCA in  time (We have to precalculate binary jumps and minimum of edge values for each jump). Total complexity is
time (We have to precalculate binary jumps and minimum of edge values for each jump). Total complexity is 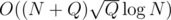
thanks
The solutions have been posted. You can read the blogpost or open the task and check the "Editorial" tab.
How to solve Subarray Medians?
O(n2). Iterate over the starting index
start. Set the ending indexendto the last possible index. Maintain a list of values (implemented with pointers to next and previous element), initially with all n numbers. Remove numbers beforestart. In the list keep a variable (pointer)mid— what is the middle value. This was how to do first for the fixedstart. Then we must moveendto the right, removing values and moving a valuemidif needed.I think I have easier solution.
Let's fix the median. Now iterate from it to the left and to the right, calculating balances (add 1 if element is bigger and -1 if it's smaller)
Now, we are median iff the balance on the left=-balance one right
I've iterated in increasing order of medians but it's not actually necessary
I didn't find all the answers one by one but it's possible if we store not sums in l/r arrays but vectors of all ends
You are using the exact formula for hash, aren't you? :)
Well, I use it, but it's easy to find all the answer using this method anyway
Oh, right, I haven't think this way. Great solution!
Iterate over the position of median. Build another array b[], where b[i] is 0 if a[i] == median, b[i] == 1 if a[i] > a[pos], and b[i] == -1 if a[i] < a[pos]. Now u have to count number of segs [L, R] such that L <= pos && R >= pos && sum[L..R] == 0 && (R — L) % 2 == 0.
I think that giving a very hard problem doesn't mean you should make other problems easier than usually. It creates a big gap and thus strange results. It's maybe better to keep other problems standard and hope that some participants will try to solve the last problem before finishing others. Possibilities:
Still, it isn't good if two last problems both require much coding. It would be nice to avoid that.
That being said, my opinion about the round is that first six problems were nice but easy. I didn't manage to solve the last problem and it was a bit sad/boring for me because other ones didn't give me much fun. Anyway, thanks for a round.
What problems are you considering 'two last'? My solution to 'Expected Tree Degrees' is pure math and ~40 lines of code.
Oh, sorry. I didn't mean "in this contest two last problems required much coding". I was writing about contests in general. I said that my opinion is: one very hard problem doesn't mean others should be easy but it's bad if two hard problems require a lot of code. This issue wasn't present in todays round of course.
For Xor Closure, could someone please elaborate this sentence from editorial a bit more?
We create a system of binary ecuations where each bit has an associated equation and each element in the input is a variable.I just saw the author solution of Expected Tree Degrees, and I believe mine's simpler. My dynamic programming is just:
The answer is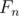 . Anyone else with the same thing?
. Anyone else with the same thing?
Can you explain it?
Well, I'm not good at probability problems so tell me if something doesn't make sense but:
Suppose we have some tree of size N and we're adding a new vertex. Let's say that we connect the new vertex to some of the previously existing ones which prior to the connection had degree K. The increase of the formula is 2 * K + 1 + 1 (1 from the new vertex of degree 1, and 2 * K + 1 from the increase of the old one with (K + 1)2 - K2)
So we get an increase of 2*K+2. Well, K is just some random degree so we can take the average of the existing degrees — which is independent of the tree structure. The average degree is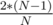 . So the increase is simply
. So the increase is simply 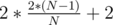 and there's the formula.
and there's the formula.
It's so simple and beautiful! Nice.
Very nice!
My solution to 'Expected Tree Degrees' (informally).
I will denote 'Random variable equal to 1 if v is parent of u and 0 otherwise' as [(v) - (u)].
(all the calulations for non-root vertex, for root it is even easier)
[deg(v)] = 1 + Σv < u[(v) - (u)]
[deg(v)2] = (1 + Σv < u[(v) - (u)])2 = 1 + 2·Σv < u[(v) - (u)] + Σv < u[(v) - (u)]2 + Σv < u, w;u ≠ w[(v) - (u)]·[(v) - (w)]
where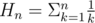 and
and 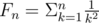
We'll try to do better on future rounds, sorry about the issues. We need to get more stable with developing the website so that we can have a dedicated team on tasks only. Since we're launched pretty recently, we have a lot of work we need to put into making the platform stable.
We some issues with the tests on the last task, so we decided to rejudge it.
So this isn't unfair to anyone, the prize you'll receive for this round will be the prize for the best rank you get before or after the rejudgement.
Were tests invalid? If not then you shouldn't rejudge. Weak tests happen but trying to fail more solutions after the contests isn't right.
Tests were invalid, since we said that the weights on edges are less than 10^5, but they were in int (they needed normalization). This is the reason for reeval actually. LHiC actually had a good solution that got WA incorrectly.
Ok, got it. And well, input validators are very important.
The tests for the last task, Yury's tree didn't respect the constraints. The weights of the edges were actually up to 10^9, not 10^5 as mentioned in the statement. We normalised these values an reevaluated the task. There are two changes in the standings: LHiC and geniucos passed the new tests and they are now 3rd and 4th, respectively.
Besides the top 5, we announced two more special prizes. We decided to award them randomly in a similar fashion to the last round. Everyone who submitted at least one correct solution entered the lottery, except the top 5. The contestant placed 6th had a weight of 5, while the one placed 194th had a weight of 1, with everyone in between linearly distributed. This round's winners are Errichto and Egor.
Congratulations all and we hope to see you soon at Round #11!