Hi , I am interested to solve a problem and I can not find a polynomial solution . How many spanning trees are in a grid graph(N x M)?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 18:52:19 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










If you're looking for an O((mn)O(1)) solution take a look at this.
Perhaps because of the special characteristics of the graph the determinant can be computed faster?
Can you explain the whole solution , please?
The answer for you question is the value of the determinant of the graph's Laplacian matrix. This matrix is computed multiplying the adjacency matrix by -1 and then adding the degree of each node on the main diagonal. Forgot to mention, after this you will have to erase the line and the column of an arbitrary vertex. You can consult this paper for proof. This will lead to a O((N * M)3) solution using Gaussian Elimination. I belive LU decomposition will work better on this kind of matrix though.
An easier particular case is when M = N.
This is the easier case? I can't even tell if this is an integer...
Let F be a field with an element ω of order n i.e. ωn = 1. Then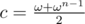 is like
is like 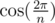 . From
. From 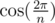 , we can get
, we can get 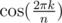 for any integer k using Chebyshev polynomials. If the base field has no such ω, we can extend this field to
for any integer k using Chebyshev polynomials. If the base field has no such ω, we can extend this field to
F[X] / (Xn - 1). Edit: X^n-1 probably doesn't work. Just generate some irreducible polynomial.I think, using that, we can solve the problem (taking word-size prime mod) in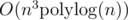 time. There is a similar formula for n ≠ m case which can be used to get similar time bound. I haven't implement any of these so I'm not sure if this really works.
time. There is a similar formula for n ≠ m case which can be used to get similar time bound. I haven't implement any of these so I'm not sure if this really works.
You can use the Kirchhoff Theorem! It has the same complexity as computing the determinant of a matrix (which is polynomial, using Gaussian Elimination).
This Spoj problem is exactly what you describe :) Maze