Hello everyone, I wrote down a problem statement in class because I was bored. Sadly, I didn't figure out its solution.
Problem:
Walid was assigned to build a network, however the required network has its own properties.
The network is divided into groups; each group is made of 2 types of nodes: Group Owners and slaves. There can be a maximum of d slaves in a group. Note: You can't have a group inside a group.
Each second, r nodes will join the network. There will be a total of m insertions.
A node can either declare itself as a group owner, or join an existing network if possible.
However, for a node to declare itself as a group owner, there will be an overhead of cost d, while joining an existing network costs an overhead of weight 1.
Walid task is to create a network with minimum overhead.
Input:
- m : Number of insertions
- r : Number of nodes joining the network
- d : Maximum number of slaves allowed per group
Output:
Print the number of groups for each t, to build a network with least cost at time m.
I think this problem is a DP problem. Any help? Thanks!











"for a node to declare itself as a group owner, there will be an overhead of cost d"
"d : Maximum number of slaves allowed per group"
are they the same number?
anyway, this problem can be solved with greedy approach.
if costd > 1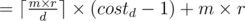
let every new node join an existing group if it can
minimum overhead
else if costd ≤ 1
let every new node declare itself as a group owner
minimum overhead = m × r × costd
you can decide which group to put new node in O(1)
so total Time complexity= O(m × r)
I think this can be done using greedy approach if overheads of all nodes are same (always x to become owner and 1 to become slave). It is always optimal to join some already existing group because it is certainly cheaper than becoming an owner (x >= 1). But in case the x's are different than this should be done using DP.