Пусть нам дан массив int a[n] . И требуется найти все коэффициенты многочлена (x+a[0])*...*(x+a[n-1]) Если считать в лоб, то будет сложность O(n^2). Есть ли способы считать быстрее? Есть ли смысл здесь применять быстрое преобразование Фурье? И есть ли другие хорошие подходы в этом случае. UPD. Как обычно считаю, что все операции производятся по модулю большого числа, если это здесь вдруг имеет значение.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
14:09:02
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
14:09:02
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 03:26:00 (i2).
Десктопная версия, переключиться на мобильную.
При поддержке
Автокомментарий: текст был обновлен пользователем Obk (предыдущая версия, новая версия, сравнить).
Как раз Фурье это и надо делать. Можно решать за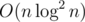
.
Изначально у нас есть n многочленов размера 1, нужно посчитать их произведение. Повторим n - 1 раз такую процедуру: возьмём два многочлена минимальной степени и перемножим с помощью FFT. Утверждается, что это будет работать именно за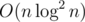
.
Можно ещё воспринимать это как умножение а-ля дерево отрезков: построим дерево отрезков на n вершинах, где в листьях будут исходные многочлены, а во внутренних вершинах -- произведение многочленов в детях. По факту это то же самое, что и абзацем выше, но так будет проще понять, откуда берётся асимптотика.
Мне понравилось первое утверждение и я решил его доказать. Для простоты будет доказываться следующее эквивалентное утверждение: есть k множеств из попарно различных элементов, общее число элементов n. На каждом шаге мы берём два наименьших множества и меняем на их объединение. Утверждается, что каждое множество будет использовано не более, чем в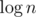
объединений.
Рассмотрим последнее объединение. Меньшее множество, очевидно, имеет размер меньше
. Большее множество либо было в наборе изначально, тогда мы вызываемся на подзадачу размера 
, либо было получено на предыдущем шаге, при этом из множеств, которые не превосходят по размеру меньшее множество. Во втором случае первое множество имеет размер от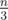 
до 
(иначе мы бы не смогли получить второе множество, чтобы в совокупности у первого и второго было n элементов), значит, мы вызываемся на две подзадачи размера 
. Отсюда очевидно, что высота любого листа в получившемся дереве не превосходит 
.
А попроще кто-нибудь умеет?
Вообще говоря, Ивану достаточно, чтобы сумма по всем элементам числа операций, в которых они побывают, была
. Это утверждение верно потому, что описанный процесс есть ничто иное, как кодирование Хаффмана, а n символов с одинаковыми вероятностями всегда можно закодировать равномерным кодом длины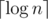 
.
Ты же пытаешься "для простоты" :) доказать более сложную оценку на максимальную длину кодового слова в кодировании Хаффмана. Там всё не так просто, но тоже можно дать точную оценку в зависимости от минимальной из вероятностей символов (в твоих терминах — O(min|Ai| / n), можно провести похожее рассуждение, но более аккуратное: http://www.work.caltech.edu/pub/Abu-Mostafa2000Huffman.pdf
Асимптотически точная оценка выглядит как
.
Ну здесь ведь вероятности не одинаковы... В случае множеств это не проблема, можно их разложить на единичные и заново собрать. С числами так уже не прокатит. Или я что-то упускаю?
P.S. А точная оценка — это, конечно, круто. Я так понимаю, тут вообще суммарное количество операций на это дело будет минимальным по всем возможным путям слияния по два множества?
Ну, человек тут спрашивает общеизвестную вещь все-таки. Я тут уже много раз в комментариях писал — если кто-то дал задачу, которая очевидным образом сводится к чему-то очень баянистому, то он сам себе дурак.
Я только сейчас случайно обратил внимание на автора задачи, из-за которой этот вопрос возник, и понял, что это ты и есть :) Задача 10/10 :thumbup:
Про то, что это задача из ongoing контеста, я совершенно согласен с adamant: слишком уж общая задача.
А как в Карацубе избавиться от логарифма? Нам же от детей нужно не просто произведение в них, но ещё и какие-то перекрёстные произведения.
Никак не надо избавляться, его там просто нет. Разделяй-и-властвуй с пересчетом за O(nc) при c > 1 работает за O(nc).
Единственное, что можно добавить, это то, что этот факт имеет мегапафосное название: МАСТА-теорема
Т.к. контест уже закончился, можно свободно его обсуждать. Я спрашивал для этой задачи: https://www.hackerrank.com/contests/w23/challenges/sasha-and-swaps-ii Кто считает, что мой вопрос очень близко к задаче и я поступил не спортивно — пусть бросит в меня камень. Um_nik, можешь показать свое решение через Карацубу?
Могу, но оно не заходит (и вообще работает медленно). Впрочем, я ни разу не сдавал Карацубу куда-либо, так что я не уверен, что это действительно правильно написанная Карацуба.
Написанный* :P
А ты хорош :)
Я взял это FFT из этого обсуждения, и ещё сначала группирую многочлены по 1000 и каждую группу умножаю без FFT. У меня 10^5 решает за 1.5 сек. Submission