Hello CodeForces Community,
I would like to invite you to participate in 101 Hack 41 will be held on Tuesday, 20 of September. The problems were set by me (Yury Bandarchuk) and josdas (Stanislav Naumov), tested by wanbo.
101 Hack is back with its 41st edition! Passionate programmers will enjoy solving algorithmic challenges. It's all about speed, accuracy and efficiency: 5 challenges in 120 minutes. Every second counts!
Top 10 winners on the leaderboard will receive a HackerRank T-Shirt.
Hope, you will participate and enjoy the problems.
Good luck && have fun!











I guess/hope one or two programmers will get full score. :) The last two problems is a little harder compared to the previous contests. Hope everyone enjoys the contest.
Can you explain 4th problem not like in an editorial? I can't understand how the editorial connected to the given problem.
Once again I find myself disagreeing with Hackerrank's philosophy in problemsetting. In Washing Plates, why do we have to print 0 if the income is negative? It adds nothing to the difficulty of the problem, you just put in one
if. If you forget about it and then find out what's wrong, you don't think "ahh, I forgot about this edge case, of course, that makes sense", but rather "why is this this sentence in the statement?" I get it, it's a paycheck, so it shouldn't be negative. But the story shouldn't be more important than the algorithm. The same goes for k>n, another pointless "haha, got you" condition. Both of these are akin to allowing cases like n=0, which we almost never see on Codeforces, for example.The 4th problem was interesting, but WTF is that editorial? Where is the proof or logic?
Let's look at the vertices, which causes maximum damage. Adoption: we remove the vertex immediately after the remove of her father. If we know two unequivocal order of vertices, then try to get them to merge and reduce the number of vertices to 1. We can do this because we know that we will remove these vertices in that order. Another statement, if we started to remove some component with dependencies, then we will remove it all, without having to switch to other components.
Now we calculate how much damage we obtain from the removal of the components size bed and the total damage sum. size * sum for this size moves. We compare the two components and understand in what order better to remove them.
In the first case size1 * sum1 + (size1 + size2) * sum2. Second size2 * sum2 + (size1 + size2) * sum1. Let's compare them. We find that quite compare: sum / size.
Now, we will support the entire structure in the set, for a maximum. And dsu for mergers
I still don't completely understand your explanation.
I got 45/80 by running a dfs, storing the optimal sequence of removals at each node, and using DP to merge the sequences of its children. Is this what you mean by "If we know two unequivocal order of vertices, then try to get them to merge and reduce the number of vertices to 1"? How do you do the merge step faster?
@-Wave-, I agree with you, next time, I will try to discard the tedious part which is not highly related to the algorithm. Because I got AC the first time very easily, so I haven't noticed that there is any problem.
Can you please explain editorial of Tree Color in more detail.
Can someone please explain how to solve the 3rd problem, Aria's Loops? I did not understand the editorial.
Let's transform the given problem to the next one:
This problem can be solved with k-combination with repetitions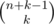
(I strongly belive, you can understand why this is the answer).
In order to transform initial problem to the problem above, .
.
you have to extract from initial N the values from 1 to k - 1 which is
Now, you can get the formula from editorial.
I read the editorial after the contest and i bounded the logic chain today in the morning.
There is an easy way to understand the formula.
We'll map each sequence (i1, i2, ..., ik) with a new sequence (a1, a2, ..., ak, ak + 1, such that a1 = i1, a2 = i2 - i1, a3 = i3 - i2 - 1, ..., ak = ik - ik - 1 - (k - 2), ak + 1 = n - (i1 + i2 + ... + ik) + 1. Now, and note that ai are positive integers. Conversely, every positive integer solution to this equation is equivalent to a sequence (i1, i2, ..., ik) that can be attained in the code. So, we just need to count the number of new sequences, which is easy, since by balls in urns formula this is just
and note that ai are positive integers. Conversely, every positive integer solution to this equation is equivalent to a sequence (i1, i2, ..., ik) that can be attained in the code. So, we just need to count the number of new sequences, which is easy, since by balls in urns formula this is just 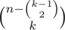 . This gives the formula.
. This gives the formula.
I think ak + 1 should be given by:
For the 3rd problem, Aria's Loop someone may find this useful
I know the post is really old, but I have to ask one more time: How to solve 4th problem? It is very interesting and I've struggled for a couple of months to solve it and no results are to be seen. I'd be grateful if someone could provide me with a complete explanation.
I found another blog regarding this problem .
The problem seems to be the same as this problem (just stated in a different manner).
This should help you solve the problem.
Thanks both of you. I will read the explanations you gave, but I'm optimist that I will understand at least one of them as they seem to be written very well.